First Steps Towards Full Model Based Motion Planning and Control of Quadrupeds: A Hybrid Zero Dynamics Approach
Paper and Code
Sep 17, 2019
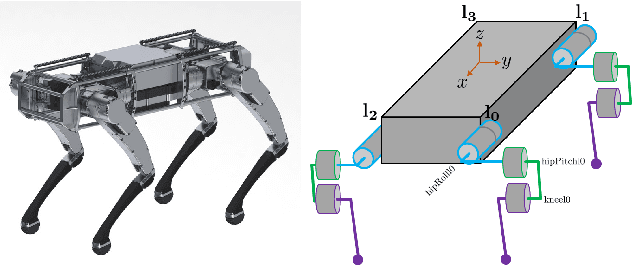
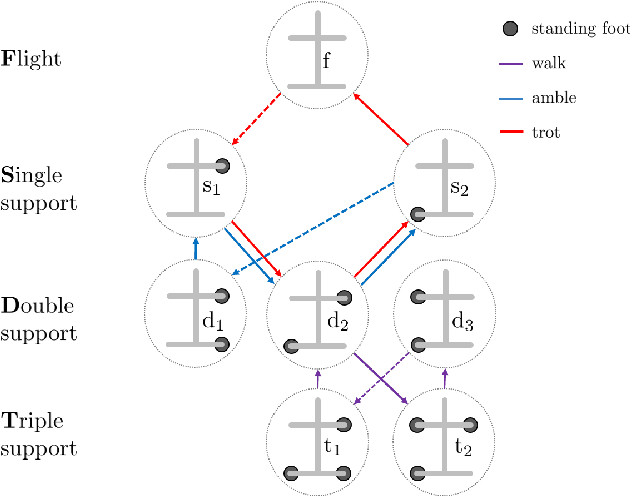

The hybrid zero dynamics (HZD) approach has become a powerful tool for the gait planning and control of bipedal robots. This paper aims to extend the HZD methods to address walking, ambling and trotting behaviors on a quadrupedal robot. We present a framework that systematically generates a wide range of optimal trajectories and then provably stabilizes them for the full-order, nonlinear and hybrid dynamical models of quadrupedal locomotion. The gait planning is addressed through a scalable nonlinear programming using direct collocation and HZD. The controller synthesis for the exponential stability is then achieved through the Poincar\'e sections analysis. In particular, we employ an iterative optimization algorithm involving linear and bilinear matrix inequalities (LMIs and BMIs) to design HZD-based controllers that guarantee the exponential stability of the fixed points for the Poincar\'e return map. The power of the framework is demonstrated through gait generation and HZD-based controller synthesis for an advanced quadruped robot, ---Vision 60, with 36 state variables and 12 control inputs. The numerical simulations as well as real world experiments confirm the validity of the proposed framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge