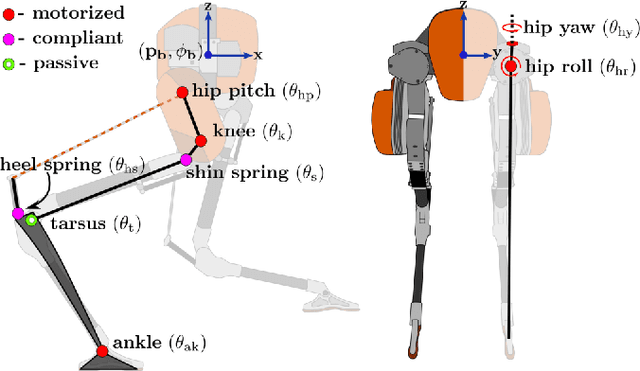
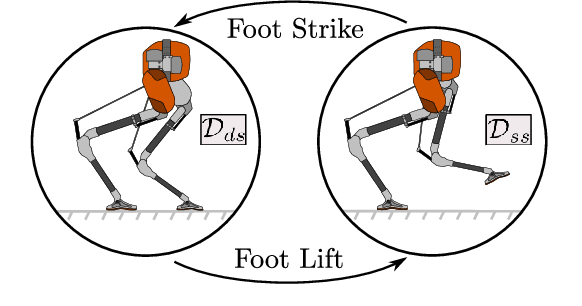
Dynamic Walking with Compliance on a Cassie Bipedal Robot

The control of bipedal robotic walking remains a challenging problem in the domains of computation and experiment, due to the multi-body dynamics and various sources of uncertainty. In recent years, there has been a rising trend towards model reduction and the design of intuitive controllers to overcome the gap between assumed model and reality. Despite its viability in practical implementation, this local representation of true dynamics naturally indicate limited scalibility towards more dynamical behaviors. With the goal of moving towards increasingly dynamic behaviors, we leverage the detailed full body dynamics to generate controllers for the robotic system which utilizes compliant elements in the passive dynamics. In this process, we present a feasible computation method that yields walking trajectories for a highly complex robotic system. Direct implementation of these results on physical hardware is also performed with minimal tuning and heuristics. We validate the suggested method by applying a consistent control scheme across simulation, optimization and experiment, the result is that the bipedal robot Cassie walks over a variety of indoor and outdoor terrains reliably.

Input to State Stability of Bipedal Walking Robots: Application to DURUS

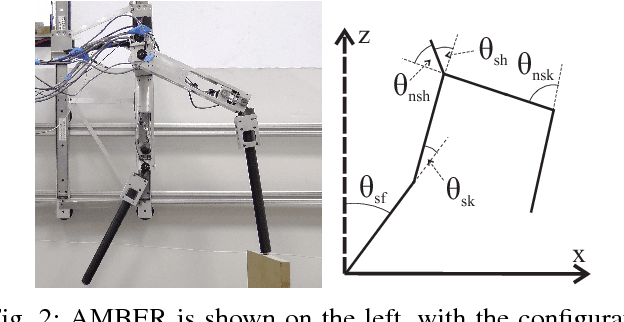
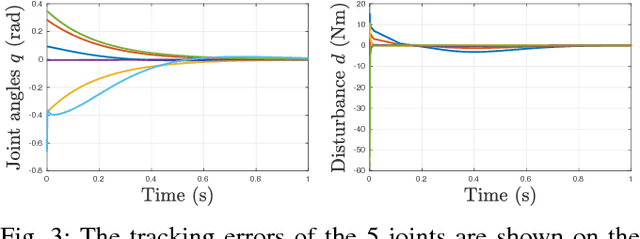
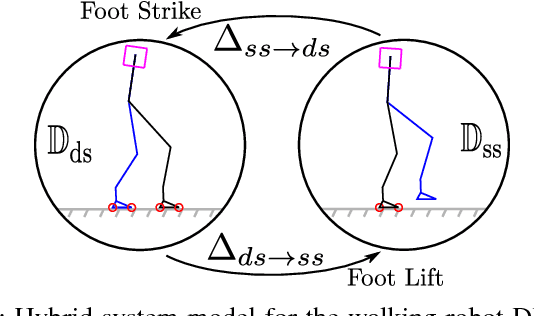
Bipedal robots are a prime example of systems which exhibit highly nonlinear dynamics, underactuation, and undergo complex dissipative impacts. This paper discusses methods used to overcome a wide variety of uncertainties, with the end result being stable bipedal walking. The principal contribution of this paper is to establish sufficiency conditions for yielding input to state stable (ISS) hybrid periodic orbits, i.e., stable walking gaits under model-based and phase-based uncertainties. In particular, it will be shown formally that exponential input to state stabilization (e-ISS) of the continuous dynamics, and hybrid invariance conditions are enough to realize stable walking in the 23-DOF bipedal robot DURUS. This main result will be supported through successful and sustained walking of the bipedal robot DURUS in a laboratory environment.