Input to State Stability of Bipedal Walking Robots: Application to DURUS
Paper and Code
Jan 02, 2018
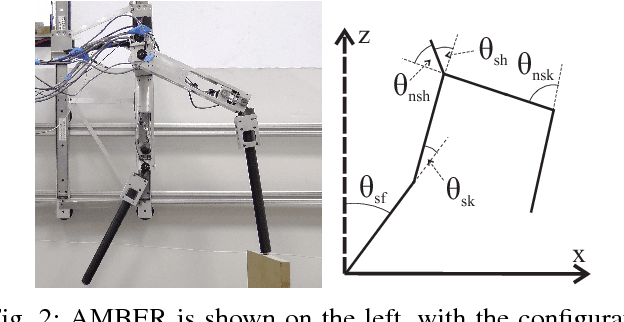
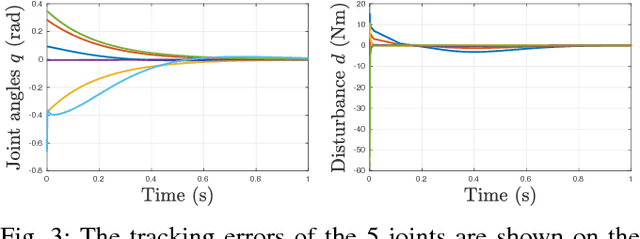
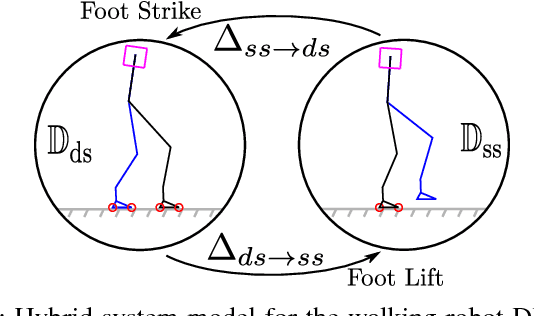
Bipedal robots are a prime example of systems which exhibit highly nonlinear dynamics, underactuation, and undergo complex dissipative impacts. This paper discusses methods used to overcome a wide variety of uncertainties, with the end result being stable bipedal walking. The principal contribution of this paper is to establish sufficiency conditions for yielding input to state stable (ISS) hybrid periodic orbits, i.e., stable walking gaits under model-based and phase-based uncertainties. In particular, it will be shown formally that exponential input to state stabilization (e-ISS) of the continuous dynamics, and hybrid invariance conditions are enough to realize stable walking in the 23-DOF bipedal robot DURUS. This main result will be supported through successful and sustained walking of the bipedal robot DURUS in a laboratory environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge