Péter L. Várkonyi
Lyapunov stability of a rigid body with two frictional contacts
Aug 09, 2016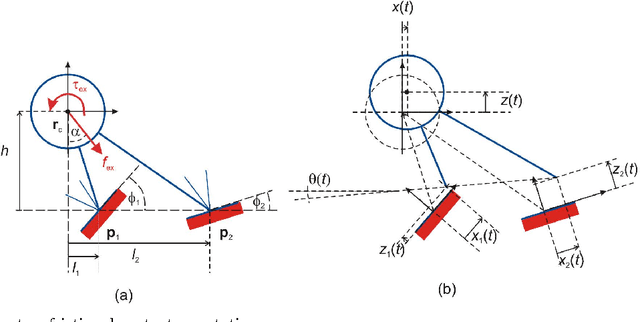
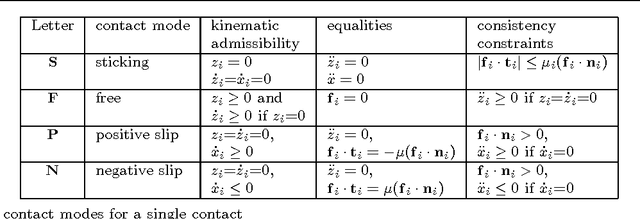
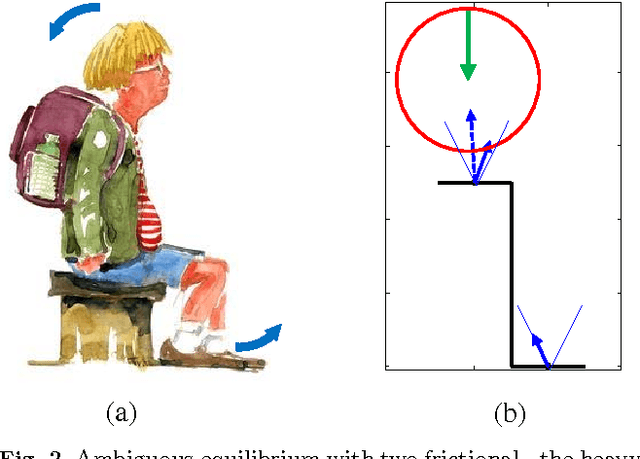
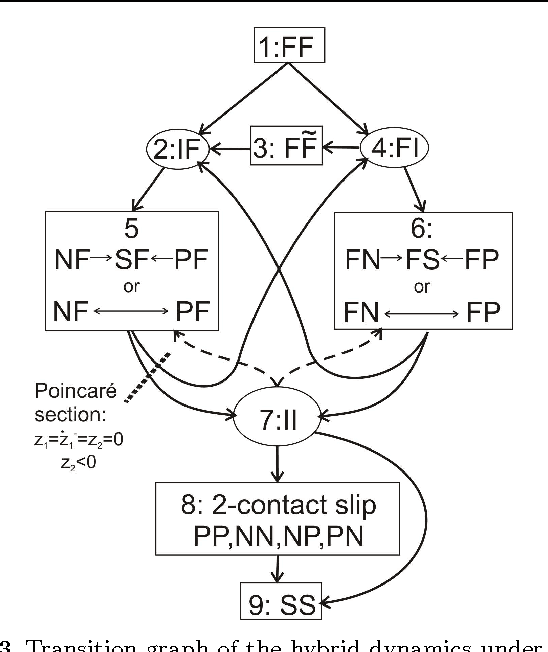
Abstract:Lyapunov stability of a mechanical system means that the dynamic response stays bounded in an arbitrarily small neighborhood of a static equilibrium configuration under small perturbations in positions and velocities. This type of stability is highly desired in robotic applications that involve multiple unilateral contacts. Nevertheless, Lyapunov stability analysis of such systems is extremely difficult, because even small perturbations may result in hybrid dynamics where the solution involves many nonsmooth transitions between different contact states. This paper concerns with Lyapunov stability analysis of a planar rigid body with two frictional unilateral contacts under inelastic impacts, for a general class of equilibrium configurations under a constant external load. The hybrid dynamics of the system under contact transitions and impacts is formulated, and a \Poincare map at two-contact states is introduced. Using invariance relations, this \Poincare map is reduced into two semi-analytic scalar functions that entirely encode the dynamic behavior of solutions under any small initial perturbation. These two functions enable determination of Lyapunov stability or instability for almost any equilibrium state. The results are demonstrated via simulation examples and by plotting stability and instability regions in two-dimensional parameter spaces that describe the contact geometry and external load.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge