Characterizing Error in Noncommutative Geometric Gait Analysis

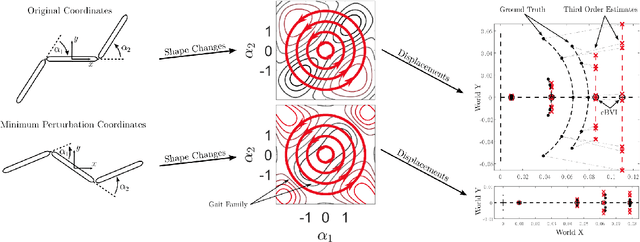
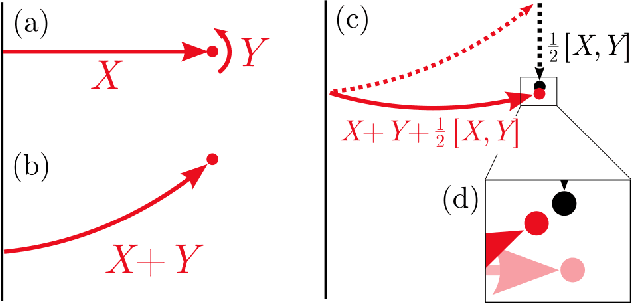
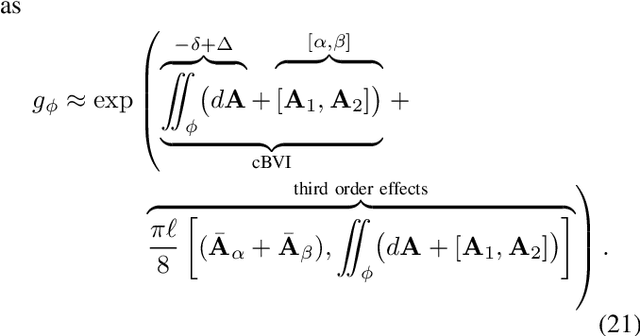
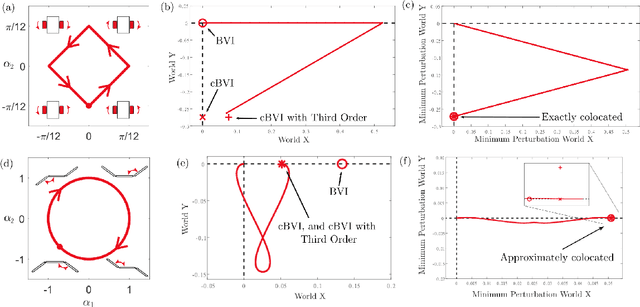
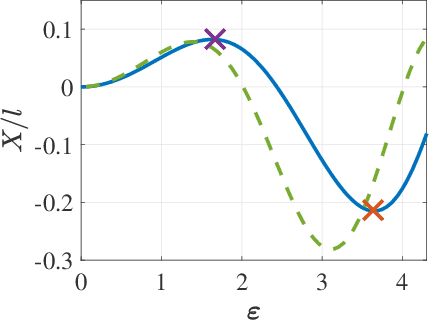
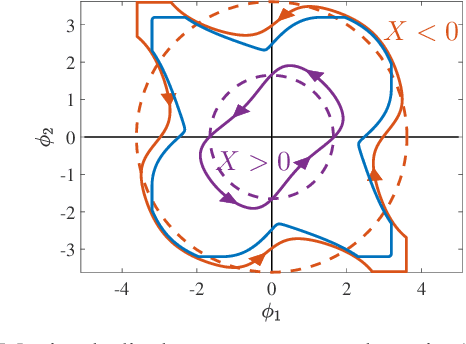
A key problem in robotic locomotion is in finding optimal shape changes to effectively displace systems through the world. Variational techniques for gait optimization require estimates of body displacement per gait cycle; however, these estimates introduce error due to unincluded high order terms. In this paper, we formulate existing estimates for displacement, and describe the contribution of low order terms to these estimates. We additionally describe the magnitude of higher (third) order effects, and identify that choice of body coordinate, gait diameter, and starting phase influence these effects. We demonstrate that variation of such parameters on two example systems (the differential drive car and Purcell swimmer) effectively manages third order contributions.

Geometric analysis of gaits and optimal control for three-link kinematic swimmers

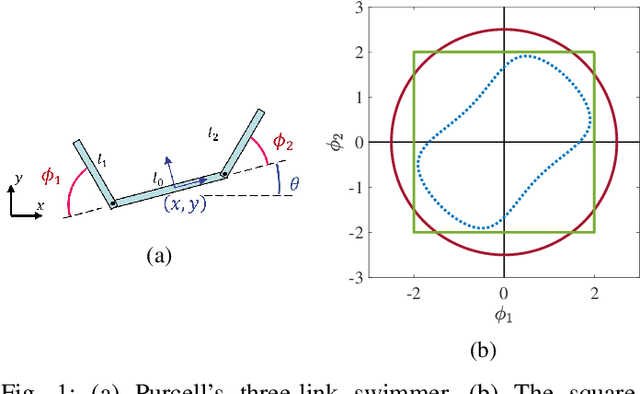
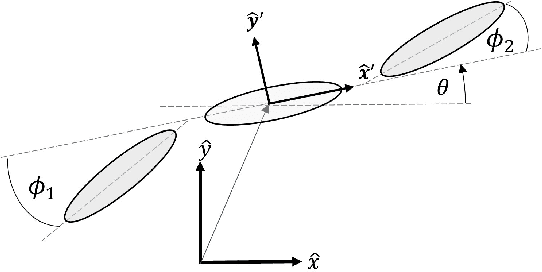
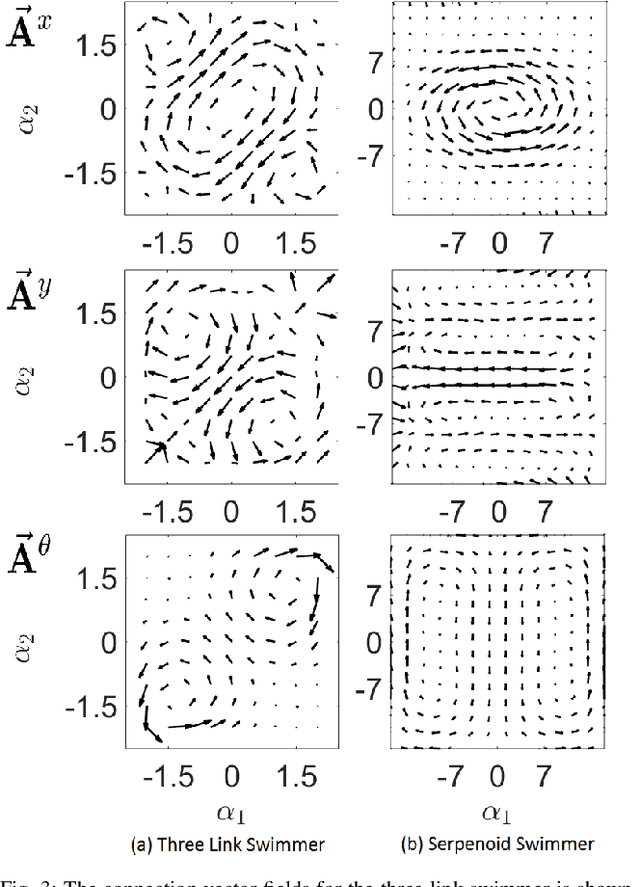
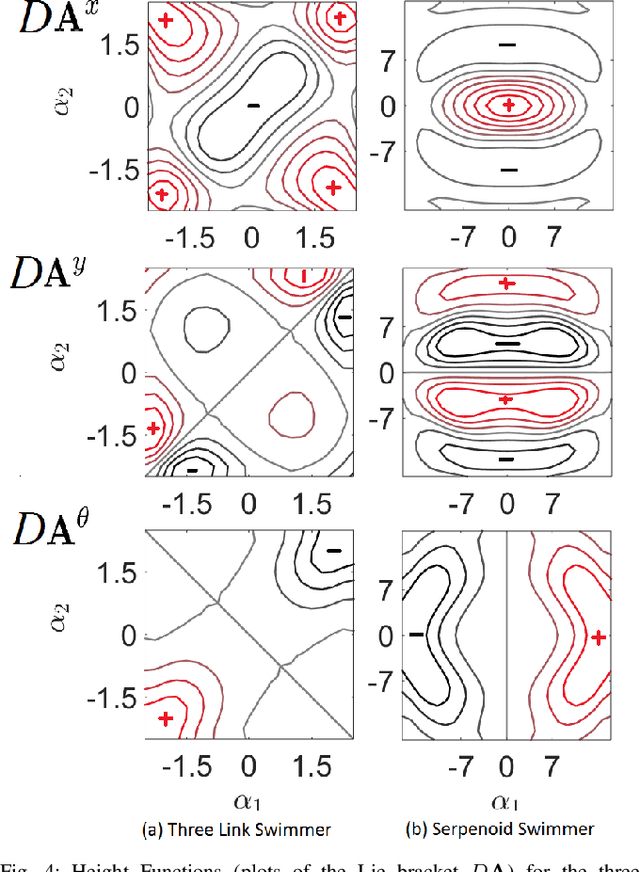
Many robotic systems locomote using gaits - periodic changes of internal shape, whose mechanical interaction with the robot`s environment generate characteristic net displacements. Prominent examples with two shape variables are the low Reynolds number 3-link "Purcell swimmer" with inputs of 2 joint angles and the "ideal fluid" swimmer. Gait analysis of these systems allows for intelligent decisions to be made about the swimmer`s locomotive properties, increasing the potential for robotic autonomy. In this work, we present comparative analysis of gait optimization using two different methods. The first method is variational approach of "Pontryagin`s maximum principle" (PMP) from optimal control theory. We apply PMP for several variants of 3-link swimmers, with and without incorporation of bounds on joint angles. The second method is differential-geometric analysis of the gaits based on curvature (total Lie bracket) of the local connection for 3-link swimmers. Using optimized body-motion coordinates, contour plots of the curvature in shape space gives visualization that enables identifying distance-optimal gaits as zero level sets. Combining and comparing results of the two methods enables better understanding of changes in existence, shape and topology of distance-optimal gait trajectories, depending on the swimmers' parameters.

Soap-bubble Optimization of Gaits

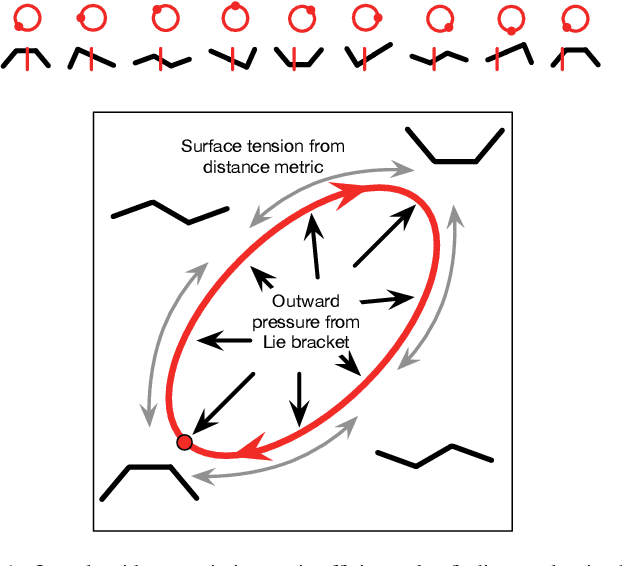
In this paper, we present a geometric variational algorithm for optimizing the gaits of kinematic locomoting systems. The dynamics of this algorithm are analogous to the physics of a soap bubble, with the system's Lie bracket supplying an "inflation pressure" that is balanced by a "surface tension" term derived from a Riemannian metric on the system's shape space. We demonstrate this optimizer on a variety of system geometries (including Purcell's swimmer) and for optimization criteria that include maximizing displacement and efficiency of motion for both translation and turning motions.