Linear Kinematics for General Constant Curvature and Torsion Manipulators

We present a novel general model that unifies the kinematics of constant curvature and constant twist continuum manipulators. Combining this kinematics with energy-based physics, we derive a linear mapping from actuator configuration to manipulator deformation that is analogous to traditional robot forward kinematics. Our model generalizes across manipulators with different sizes, types of bending, and types of actuators, without the need for parameter re-fitting. The combination of generality and linearity makes the model useful for control and planning algorithms. Finally, our model is shown to be accurate through experimental validation on manipulators with pneumatic artificial muscles.

Optimal Gait Families using Lagrange Multiplier Method

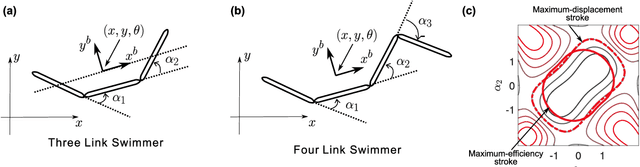
The robotic locomotion community is interested in optimal gaits for control. Based on the optimization criterion, however, there could be a number of possible optimal gaits. For example, the optimal gait for maximizing displacement with respect to cost is quite different from the maximum displacement optimal gait. Beyond these two general optimal gaits, we believe that the optimal gait should deal with various situations for high-resolution of motion planning, e.g., steering the robot or moving in "baby steps." As the step size or steering ratio increases or decreases, the optimal gaits will slightly vary by the geometric relationship and they will form the families of gaits. In this paper, we explored the geometrical framework across these optimal gaits having different step sizes in the family via the Lagrange multiplier method. Based on the structure, we suggest an optimal locus generator that solves all related optimal gaits in the family instead of optimizing each gait respectively. By applying the optimal locus generator to two simplified swimmers in drag-dominated environments, we verify the behavior of the optimal locus generator.

Characterizing Error in Noncommutative Geometric Gait Analysis

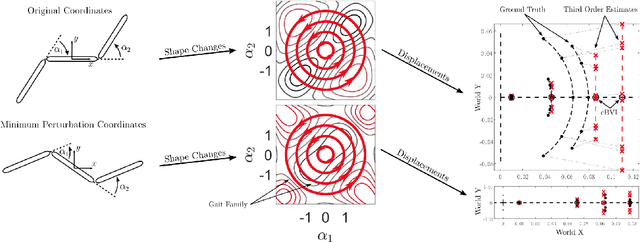
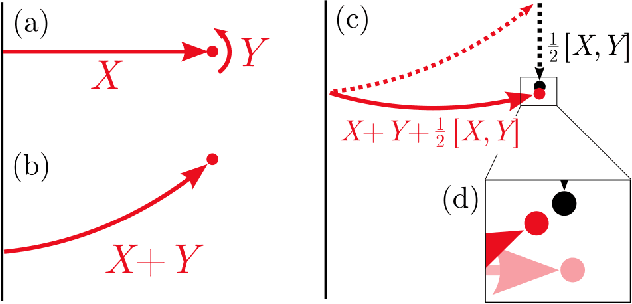
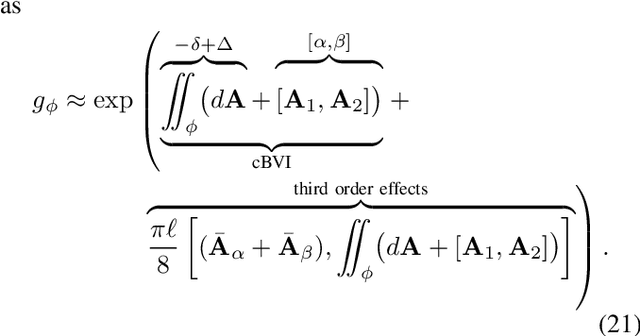
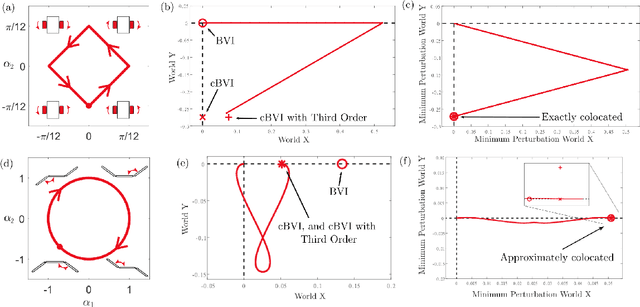
A key problem in robotic locomotion is in finding optimal shape changes to effectively displace systems through the world. Variational techniques for gait optimization require estimates of body displacement per gait cycle; however, these estimates introduce error due to unincluded high order terms. In this paper, we formulate existing estimates for displacement, and describe the contribution of low order terms to these estimates. We additionally describe the magnitude of higher (third) order effects, and identify that choice of body coordinate, gait diameter, and starting phase influence these effects. We demonstrate that variation of such parameters on two example systems (the differential drive car and Purcell swimmer) effectively manages third order contributions.