Optimal Gait Families using Lagrange Multiplier Method
Paper and Code
Oct 07, 2022

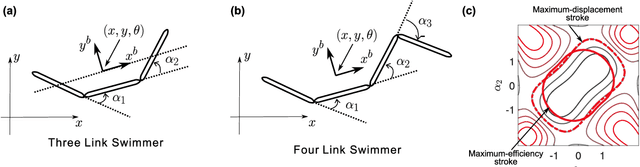

The robotic locomotion community is interested in optimal gaits for control. Based on the optimization criterion, however, there could be a number of possible optimal gaits. For example, the optimal gait for maximizing displacement with respect to cost is quite different from the maximum displacement optimal gait. Beyond these two general optimal gaits, we believe that the optimal gait should deal with various situations for high-resolution of motion planning, e.g., steering the robot or moving in "baby steps." As the step size or steering ratio increases or decreases, the optimal gaits will slightly vary by the geometric relationship and they will form the families of gaits. In this paper, we explored the geometrical framework across these optimal gaits having different step sizes in the family via the Lagrange multiplier method. Based on the structure, we suggest an optimal locus generator that solves all related optimal gaits in the family instead of optimizing each gait respectively. By applying the optimal locus generator to two simplified swimmers in drag-dominated environments, we verify the behavior of the optimal locus generator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge