Soap-bubble Optimization of Gaits
Paper and Code
Oct 26, 2016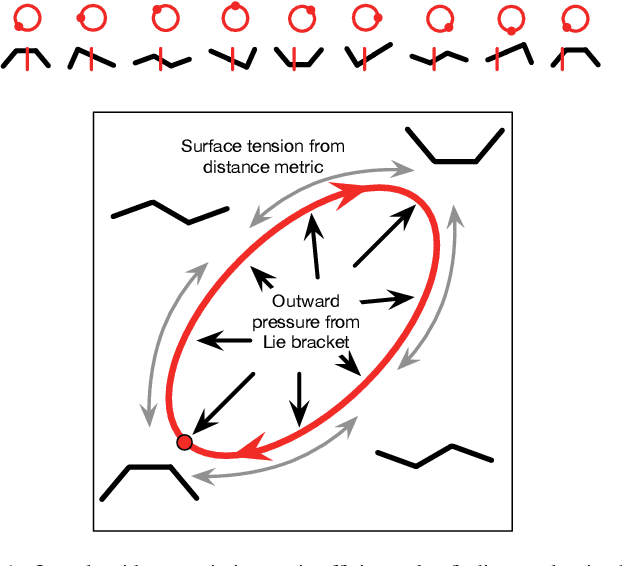

In this paper, we present a geometric variational algorithm for optimizing the gaits of kinematic locomoting systems. The dynamics of this algorithm are analogous to the physics of a soap bubble, with the system's Lie bracket supplying an "inflation pressure" that is balanced by a "surface tension" term derived from a Riemannian metric on the system's shape space. We demonstrate this optimizer on a variety of system geometries (including Purcell's swimmer) and for optimization criteria that include maximizing displacement and efficiency of motion for both translation and turning motions.
* Accepted for the Proceedings of the 55th IEEE Conference on Decision
and Control, December 2016
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge