Experimental Verification of Stability Theory for a Planar Rigid Body with Two Unilateral Frictional Contacts
Paper and Code
Aug 24, 2020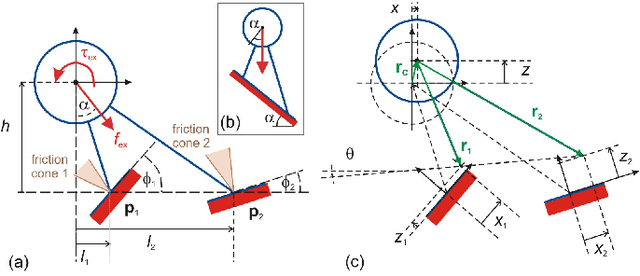
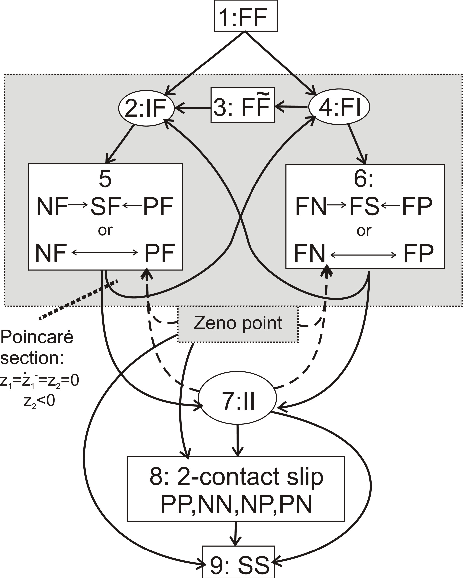
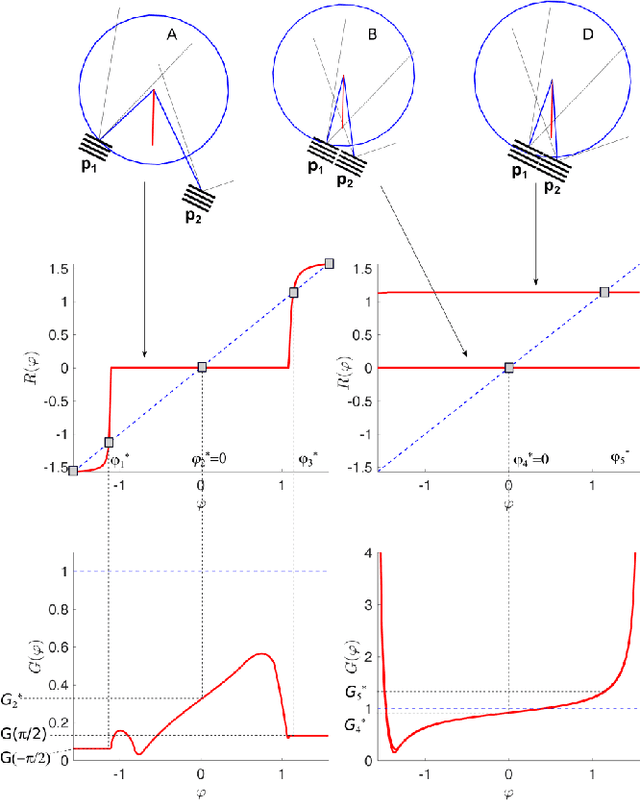
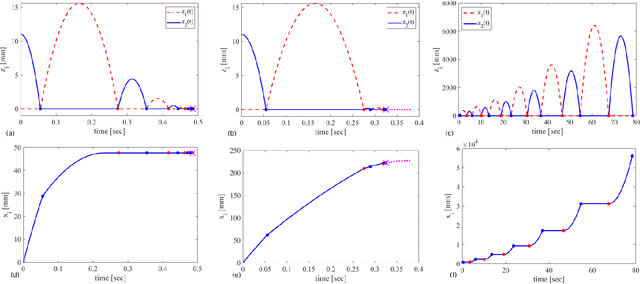
Stability of equilibrium states in mechanical systems with multiple unilateral frictional contacts is an important practical requirement, with high relevance for robotic applications. In our previous work, we theoretically analyzed finite-time Lyapunov stability for a minimal model of planar rigid body with two frictional point contacts. Assuming inelastic impacts and Coulomb friction, conditions for stability and instability of an equilibrium configuration have been derived. In this work, we present for the first time an experimental demonstration of this stability theory, using a variable-structure rigid ''biped'' with frictional footpads on an inclined plane. By changing the biped's center-of-mass location, we attain different equilibrium states, which respond to small perturbations by divergence or convergence, showing remarkable agreement with the predictions of the stability theory. Using high-speed recording of video movies, good quantitative agreement between experiments and numerical simulations is obtained, and limitations of the rigid-body model and inelastic impact assumptions are also studied. The results prove the utility and practical value of our stability theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge