Yanhao Yang
Pose Estimation of a Thruster-Driven Bioinspired Multi-Link Robot
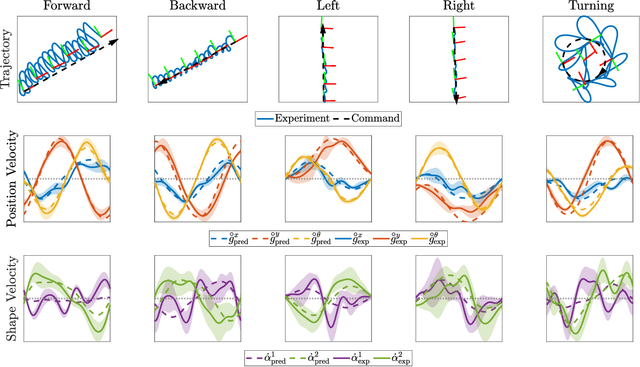
Oct 01, 2025Abstract:This work demonstrates pose (position and shape) estimation for a free-floating, bioinspired multi-link robot with unactuated joints, link-mounted thrusters for control, and a single gyroscope per link, resulting in an underactuated, minimally sensed platform. Through a proof-of-concept hardware experiment and offline Kalman filter analysis, we show that the robot's pose can be reliably estimated. State estimation is performed using an unscented Kalman filter augmented with Gaussian process residual learning to compensate for non-zero-mean, non-Gaussian noise. We further show that a filter trained on a multi-gait dataset (forward, backward, left, right, and turning) performs comparably to one trained on a larger forward-gait-only dataset when both are evaluated on the same forward-gait test trajectory. These results reveal overlap in the gait input space, which can be exploited to reduce training data requirements while enhancing the filter's generalizability across multiple gaits.
Geometric Gait Optimization for Kinodynamic Systems Using a Lie Group Integrator
Apr 27, 2025
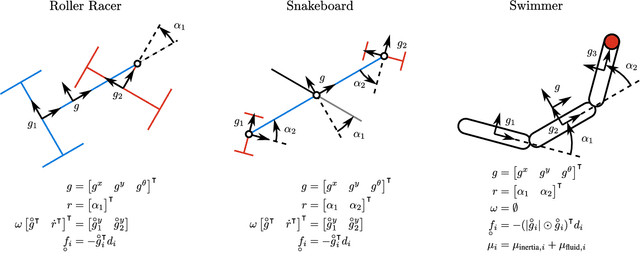
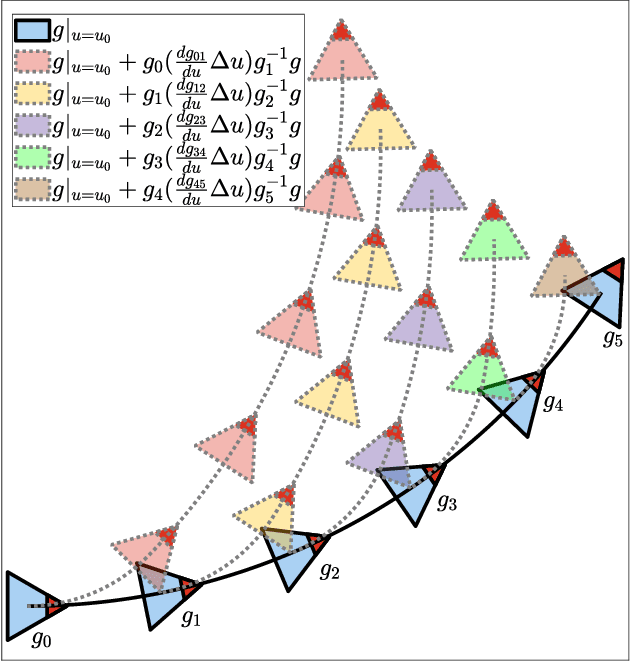
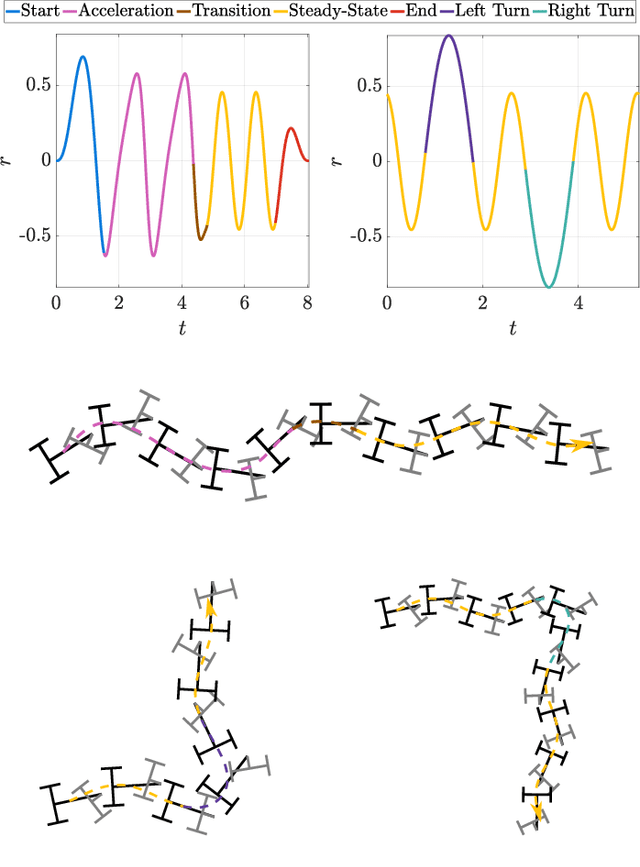
Abstract:This paper presents a gait optimization and motion planning framework for a class of locomoting systems with mixed kinematic and dynamic properties. Using Lagrangian reduction and differential geometry, we derive a general dynamic model that incorporates second-order dynamics and nonholonomic constraints, applicable to kinodynamic systems such as wheeled robots with nonholonomic constraints as well as swimming robots with nonisotropic fluid-added inertia and hydrodynamic drag. Building on Lie group integrators and group symmetries, we develop a variational gait optimization method for kinodynamic systems. By integrating multiple gaits and their transitions, we construct comprehensive motion plans that enable a wide range of motions for these systems. We evaluate our framework on three representative examples: roller racer, snakeboard, and swimmer. Simulation and hardware experiments demonstrate diverse motions, including acceleration, steady-state maintenance, gait transitions, and turning. The results highlight the effectiveness of the proposed method and its potential for generalization to other biological and robotic locomoting systems.
Geometric Data-Driven Multi-Jet Locomotion Inspired by Salps
Mar 11, 2025

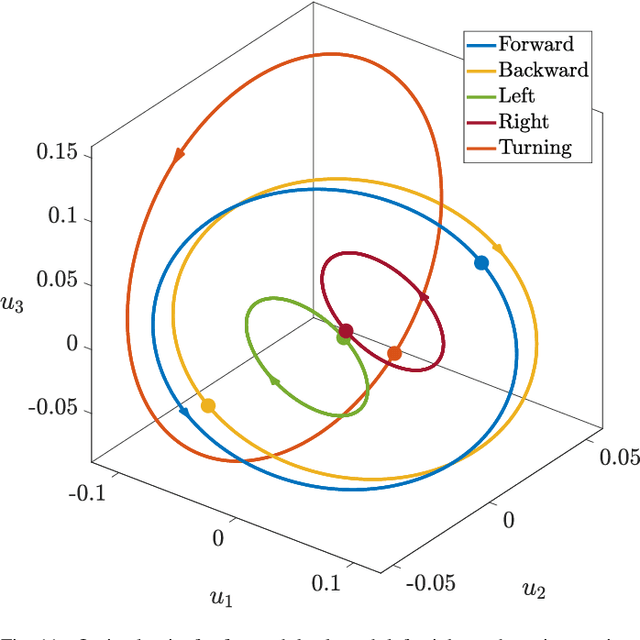
Abstract:Salps are marine animals consisting of chains of jellyfish-like units. Their capacity for effective underwater undulatory locomotion through coordinating multi-jet propulsion has aroused significant interest in the field of robotics and inspired extensive research including design, modeling, and control. In this paper, we conduct a comprehensive analysis of the locomotion of salp-like systems using the robotic platform "LandSalp" based on geometric mechanics, including mechanism design, dynamic modeling, system identification, and motion planning and control. Our work takes a step toward a better understanding of salps' underwater locomotion and provides a clear path for extending these insights to more complex and capable underwater robotic systems. Furthermore, this study illustrates the effectiveness of geometric mechanics in bio-inspired robots for efficient data-driven locomotion modeling, demonstrated by learning the dynamics of LandSalp from only 3 minutes of experimental data. Lastly, we extend the geometric mechanics principles to multi-jet propulsion systems with stability considerations and validate the theory through experiments on the LandSalp hardware.
Towards Geometric Motion Planning for High-Dimensional Systems: Gait-Based Coordinate Optimization and Local Metrics
Sep 16, 2023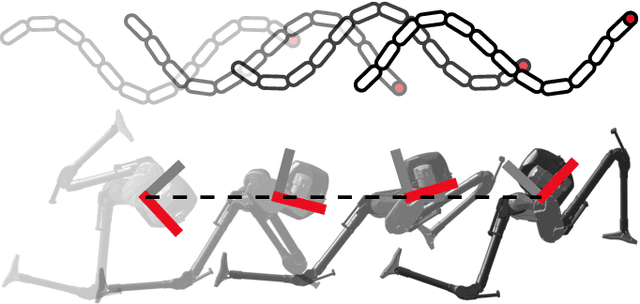
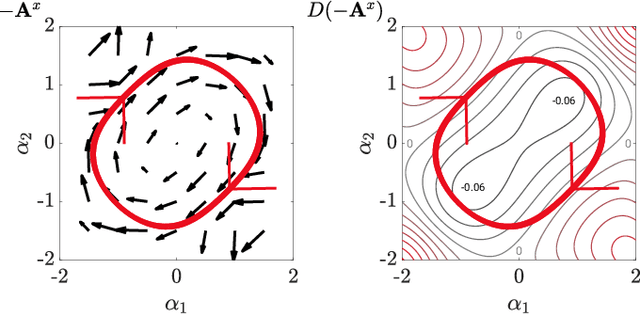
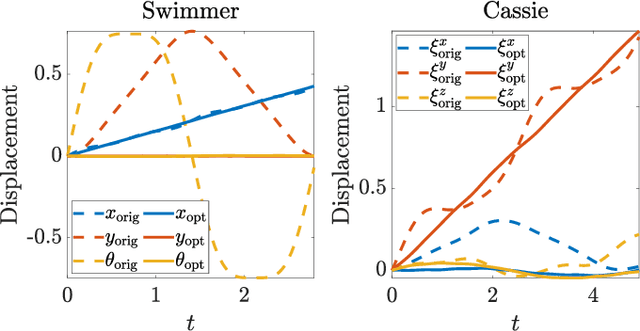
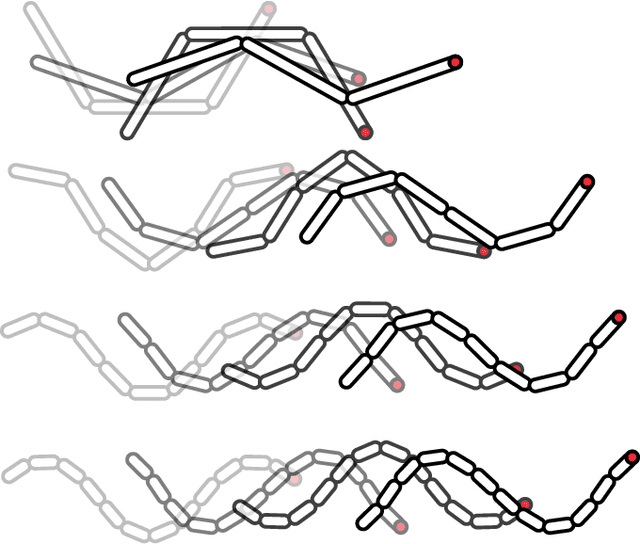
Abstract:Geometric motion planning offers effective and interpretable gait analysis and optimization tools for locomoting systems. However, due to the curse of dimensionality in coordinate optimization, a key component of geometric motion planning, it is almost infeasible to apply current geometric motion planning to high-dimensional systems. In this paper, we propose a gait-based coordinate optimization method that overcomes the curse of dimensionality. We also identify a unified geometric representation of locomotion by generalizing various nonholonomic constraints into local metrics. By combining these two approaches, we take a step towards geometric motion planning for high-dimensional systems. We test our method in two classes of high-dimensional systems - low Reynolds number swimmers and free-falling Cassie - with up to 11-dimensional shape variables. The resulting optimal gait in the high-dimensional system shows better efficiency compared to that of the reduced-order model. Furthermore, we provide a geometric optimality interpretation of the optimal gait.
Geometric Gait Optimization for Inertia-Dominated Systems With Nonzero Net Momentum
Sep 13, 2023

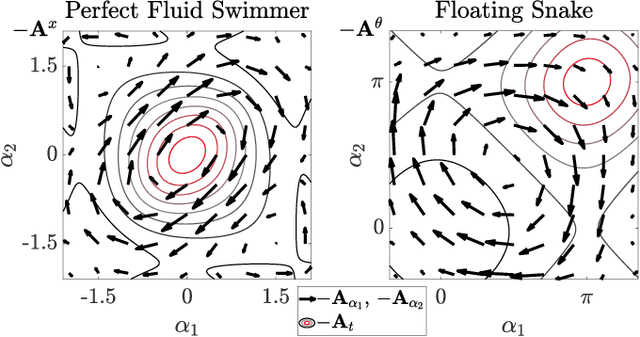
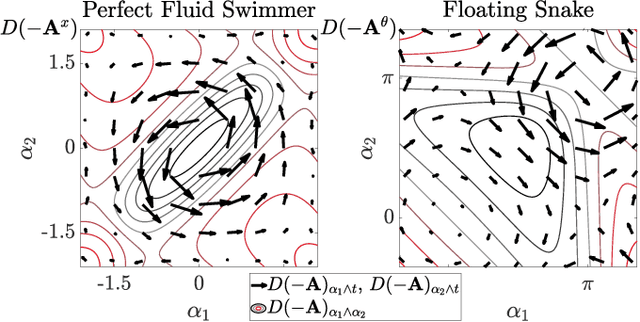
Abstract:Inertia-dominated mechanical systems can achieve net displacement by 1) periodically changing their shape (known as kinematic gait) and 2) adjusting their inertia distribution to utilize the existing nonzero net momentum (known as momentum gait). Therefore, finding the gait that most effectively utilizes the two types of locomotion in terms of the magnitude of the net momentum is a significant topic in the study of locomotion. For kinematic locomotion with zero net momentum, the geometry of optimal gaits is expressed as the equilibria of system constraint curvature flux through the surface bounded by the gait, and the cost associated with executing the gait in the metric space. In this paper, we identify the geometry of optimal gaits with nonzero net momentum effects by lifting the gait description to a time-parameterized curve in shape-time space. We also propose the variational gait optimization algorithm corresponding to the lifted geometric structure, and identify two distinct patterns in the optimal motion, determined by whether or not the kinematic and momentum gaits are concentric. The examples of systems with and without fluid-added mass demonstrate that the proposed algorithm can efficiently solve forward and turning locomotion gaits in the presence of nonzero net momentum. At any given momentum and effort limit, the proposed optimal gait that takes into account both momentum and kinematic effects outperforms the reference gaits that each only considers one of these effects.
Proprioception and Tail Control Enable Extreme Terrain Traversal by Quadruped Robots
Mar 08, 2023



Abstract:Legged robots leverage ground contacts and the reaction forces they provide to achieve agile locomotion. However, uncertainty coupled with contact discontinuities can lead to failure, especially in real-world environments with unexpected height variations such as rocky hills or curbs. To enable dynamic traversal of extreme terrain, this work introduces 1) a proprioception-based gait planner for estimating unknown hybrid events due to elevation changes and responding by modifying contact schedules and planned footholds online, and 2) a two-degree-of-freedom tail for improving contact-independent control and a corresponding decoupled control scheme for better versatility and efficiency. Simulation results show that the gait planner significantly improves stability under unforeseen terrain height changes compared to methods that assume fixed contact schedules and footholds. Further, testing shows the tail is most effective at maintaining stability when encountering a terrain change with an initial angular disturbance. The results show that these approaches work synergistically to stabilize locomotion with elevation changes up to 1.5 times the leg length and tilted initial states.
Adaptive Complexity Model Predictive Control
Sep 06, 2022



Abstract:This work introduces a formulation of model predictive control (MPC) which adaptively reasons about the complexity of the model based on the task while maintaining feasibility and stability guarantees. Existing MPC implementations often handle computational complexity by shortening prediction horizons or simplifying models, both of which can result in instability. Inspired by related approaches in behavioral economics, motion planning, and biomechanics, our method solves MPC problems with a simple model for dynamics and constraints over regions of the horizon where such a model is feasible and a complex model where it is not. The approach leverages an interleaving of planning and execution to iteratively identify these regions, which can be safely simplified if they satisfy an exact template/anchor relationship. We show that this method does not compromise the stability and feasibility properties of the system, and measure performance in simulation experiments on a quadrupedal robot executing agile behaviors over terrains of interest. We find that this adaptive method enables more agile motion and expands the range of executable tasks compared to fixed-complexity implementations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge