Optimal Control Approach for Gait Transition with Riemannian Splines
Paper and Code
Sep 13, 2024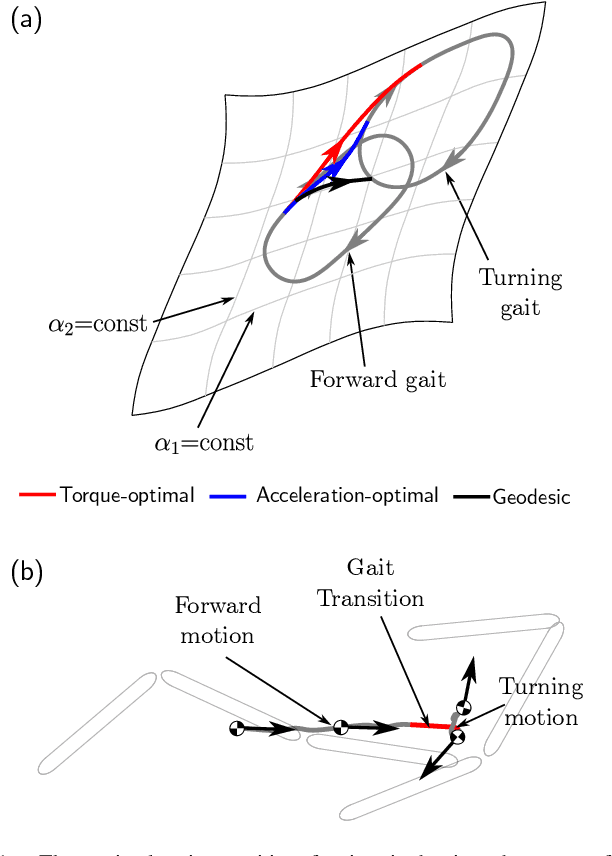
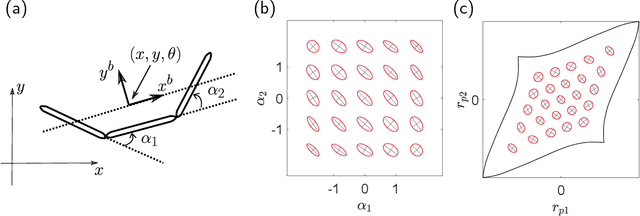
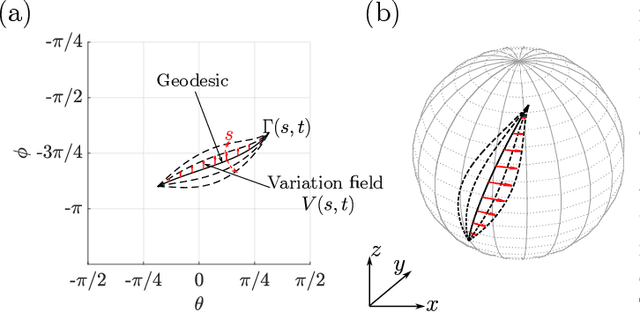
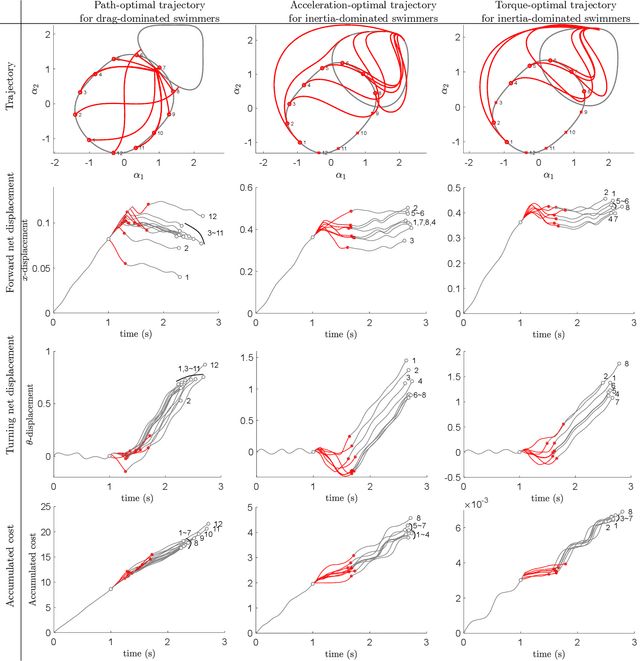
Robotic locomotion often relies on sequenced gaits to efficiently convert control input into desired motion. Despite extensive studies on gait optimization, achieving smooth and efficient gait transitions remains challenging. In this paper, we propose a general solver based on geometric optimal control methods, leveraging insights from previous works on gait efficiency. Building upon our previous work, we express the effort to execute the trajectory as distinct geometric objects, transforming the optimization problems into boundary value problems. To validate our approach, we generate gait transition trajectories for three-link swimmers across various fluid environments. This work provides insights into optimal trajectory geometries and mechanical considerations for robotic locomotion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge