Reza Zadeh
Detecting Glaucoma Using 3D Convolutional Neural Network of Raw SD-OCT Optic Nerve Scans
Oct 14, 2019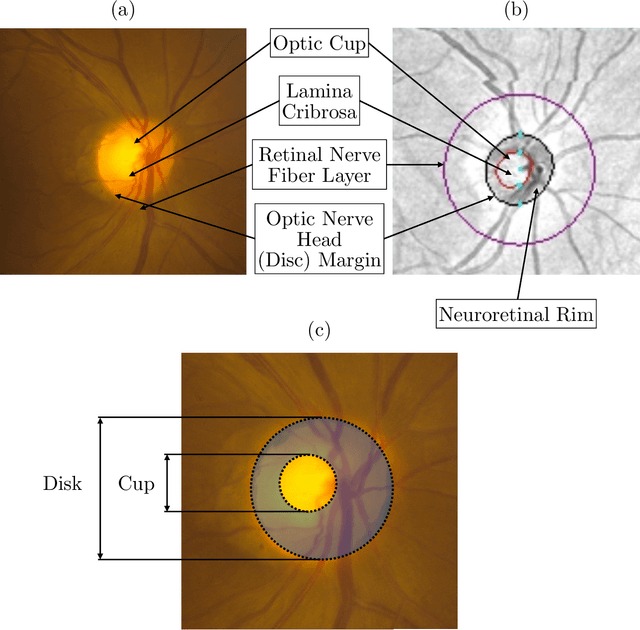

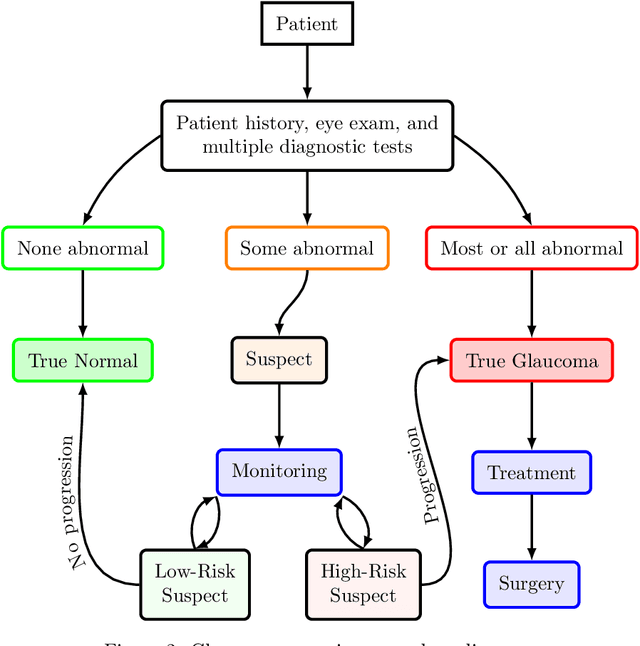

Abstract:We propose developing and validating a three-dimensional (3D) deep learning system using the entire unprocessed OCT optic nerve volumes to distinguish true glaucoma from normals in order to discover any additional imaging biomarkers within the cube through saliency mapping. The algorithm has been validated against 4 additional distinct datasets from different countries using multimodal test results to define glaucoma rather than just the OCT alone. 2076 OCT (Cirrus SD-OCT, Carl Zeiss Meditec, Dublin, CA) cube scans centered over the optic nerve, of 879 eyes (390 healthy and 489 glaucoma) from 487 patients, age 18-84 years, were exported from the Glaucoma Clinic Imaging Database at the Byers Eye Institute, Stanford University, from March 2010 to December 2017. A 3D deep neural network was trained and tested on this unique OCT optic nerve head dataset from Stanford. A total of 3620 scans (all obtained using the Cirrus SD-OCT device) from 1458 eyes obtained from 4 different institutions, from United States (943 scans), Hong Kong (1625 scans), India (672 scans), and Nepal (380 scans) were used for external evaluation. The 3D deep learning system achieved an area under the receiver operation characteristics curve (AUROC) of 0.8883 in the primary Stanford test set identifying true normal from true glaucoma. The system obtained AUROCs of 0.8571, 0.7695, 0.8706, and 0.7965 on OCT cubes from United States, Hong Kong, India, and Nepal, respectively. We also analyzed the performance of the model separately for each myopia severity level as defined by spherical equivalent and the model was able to achieve F1 scores of 0.9673, 0.9491, and 0.8528 on severe, moderate, and mild myopia cases, respectively. Saliency map visualizations highlighted a significant association between the optic nerve lamina cribrosa region in the glaucoma group.
FusionNet: 3D Object Classification Using Multiple Data Representations
Nov 27, 2016
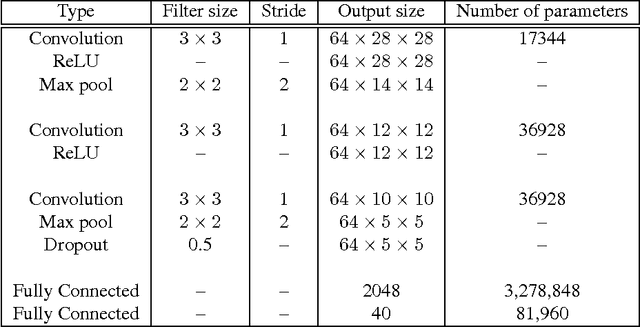
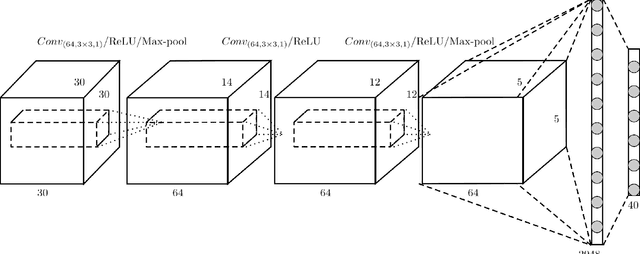
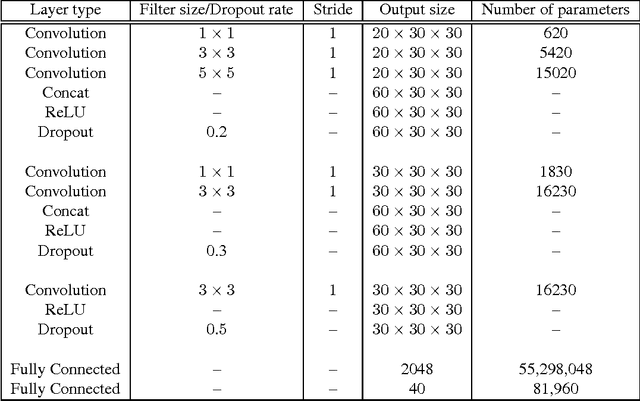
Abstract:High-quality 3D object recognition is an important component of many vision and robotics systems. We tackle the object recognition problem using two data representations, to achieve leading results on the Princeton ModelNet challenge. The two representations: 1. Volumetric representation: the 3D object is discretized spatially as binary voxels - $1$ if the voxel is occupied and $0$ otherwise. 2. Pixel representation: the 3D object is represented as a set of projected 2D pixel images. Current leading submissions to the ModelNet Challenge use Convolutional Neural Networks (CNNs) on pixel representations. However, we diverge from this trend and additionally, use Volumetric CNNs to bridge the gap between the efficiency of the above two representations. We combine both representations and exploit them to learn new features, which yield a significantly better classifier than using either of the representations in isolation. To do this, we introduce new Volumetric CNN (V-CNN) architectures.
MLlib: Machine Learning in Apache Spark
May 26, 2015

Abstract:Apache Spark is a popular open-source platform for large-scale data processing that is well-suited for iterative machine learning tasks. In this paper we present MLlib, Spark's open-source distributed machine learning library. MLlib provides efficient functionality for a wide range of learning settings and includes several underlying statistical, optimization, and linear algebra primitives. Shipped with Spark, MLlib supports several languages and provides a high-level API that leverages Spark's rich ecosystem to simplify the development of end-to-end machine learning pipelines. MLlib has experienced a rapid growth due to its vibrant open-source community of over 140 contributors, and includes extensive documentation to support further growth and to let users quickly get up to speed.
Generalized Low Rank Models
May 05, 2015
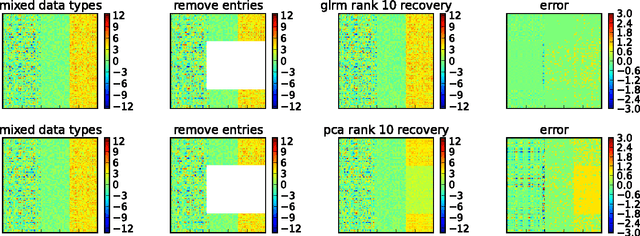


Abstract:Principal components analysis (PCA) is a well-known technique for approximating a tabular data set by a low rank matrix. Here, we extend the idea of PCA to handle arbitrary data sets consisting of numerical, Boolean, categorical, ordinal, and other data types. This framework encompasses many well known techniques in data analysis, such as nonnegative matrix factorization, matrix completion, sparse and robust PCA, $k$-means, $k$-SVD, and maximum margin matrix factorization. The method handles heterogeneous data sets, and leads to coherent schemes for compressing, denoising, and imputing missing entries across all data types simultaneously. It also admits a number of interesting interpretations of the low rank factors, which allow clustering of examples or of features. We propose several parallel algorithms for fitting generalized low rank models, and describe implementations and numerical results.
Factorbird - a Parameter Server Approach to Distributed Matrix Factorization
Nov 03, 2014



Abstract:We present Factorbird, a prototype of a parameter server approach for factorizing large matrices with Stochastic Gradient Descent-based algorithms. We designed Factorbird to meet the following desiderata: (a) scalability to tall and wide matrices with dozens of billions of non-zeros, (b) extensibility to different kinds of models and loss functions as long as they can be optimized using Stochastic Gradient Descent (SGD), and (c) adaptability to both batch and streaming scenarios. Factorbird uses a parameter server in order to scale to models that exceed the memory of an individual machine, and employs lock-free Hogwild!-style learning with a special partitioning scheme to drastically reduce conflicting updates. We also discuss other aspects of the design of our system such as how to efficiently grid search for hyperparameters at scale. We present experiments of Factorbird on a matrix built from a subset of Twitter's interaction graph, consisting of more than 38 billion non-zeros and about 200 million rows and columns, which is to the best of our knowledge the largest matrix on which factorization results have been reported in the literature.
Matrix Completion and Low-Rank SVD via Fast Alternating Least Squares
Oct 09, 2014



Abstract:The matrix-completion problem has attracted a lot of attention, largely as a result of the celebrated Netflix competition. Two popular approaches for solving the problem are nuclear-norm-regularized matrix approximation (Candes and Tao, 2009, Mazumder, Hastie and Tibshirani, 2010), and maximum-margin matrix factorization (Srebro, Rennie and Jaakkola, 2005). These two procedures are in some cases solving equivalent problems, but with quite different algorithms. In this article we bring the two approaches together, leading to an efficient algorithm for large matrix factorization and completion that outperforms both of these. We develop a software package "softImpute" in R for implementing our approaches, and a distributed version for very large matrices using the "Spark" cluster programming environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge