Results of the NeurIPS'21 Challenge on Billion-Scale Approximate Nearest Neighbor Search

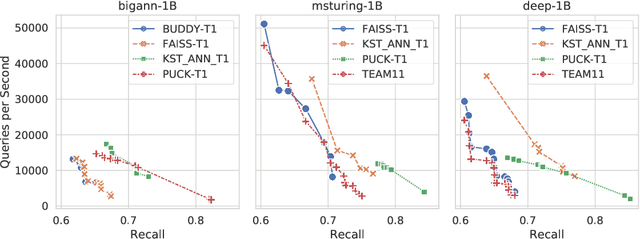
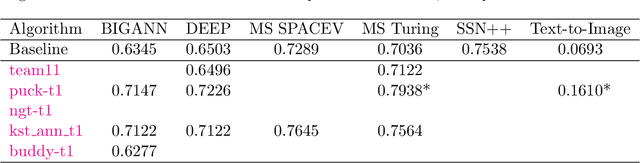
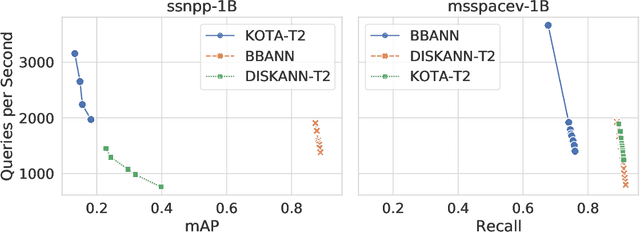
Despite the broad range of algorithms for Approximate Nearest Neighbor Search, most empirical evaluations of algorithms have focused on smaller datasets, typically of 1 million points~\citep{Benchmark}. However, deploying recent advances in embedding based techniques for search, recommendation and ranking at scale require ANNS indices at billion, trillion or larger scale. Barring a few recent papers, there is limited consensus on which algorithms are effective at this scale vis-\`a-vis their hardware cost. This competition compares ANNS algorithms at billion-scale by hardware cost, accuracy and performance. We set up an open source evaluation framework and leaderboards for both standardized and specialized hardware. The competition involves three tracks. The standard hardware track T1 evaluates algorithms on an Azure VM with limited DRAM, often the bottleneck in serving billion-scale indices, where the embedding data can be hundreds of GigaBytes in size. It uses FAISS~\citep{Faiss17} as the baseline. The standard hardware track T2 additional allows inexpensive SSDs in addition to the limited DRAM and uses DiskANN~\citep{DiskANN19} as the baseline. The specialized hardware track T3 allows any hardware configuration, and again uses FAISS as the baseline. We compiled six diverse billion-scale datasets, four newly released for this competition, that span a variety of modalities, data types, dimensions, deep learning models, distance functions and sources. The outcome of the competition was ranked leaderboards of algorithms in each track based on recall at a query throughput threshold. Additionally, for track T3, separate leaderboards were created based on recall as well as cost-normalized and power-normalized query throughput.

FreshDiskANN: A Fast and Accurate Graph-Based ANN Index for Streaming Similarity Search

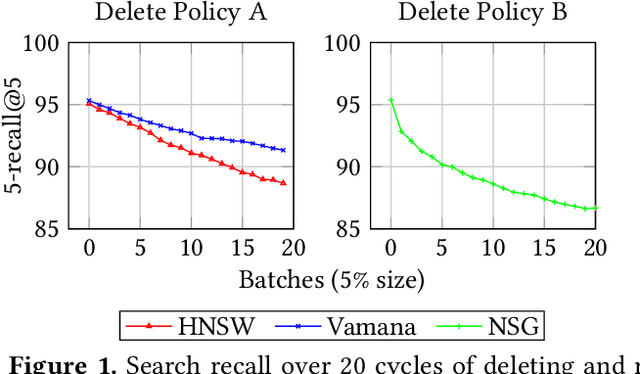
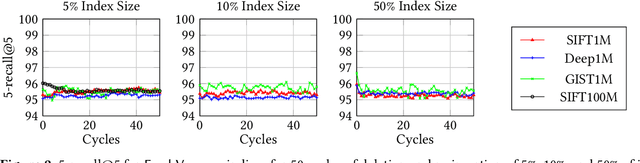
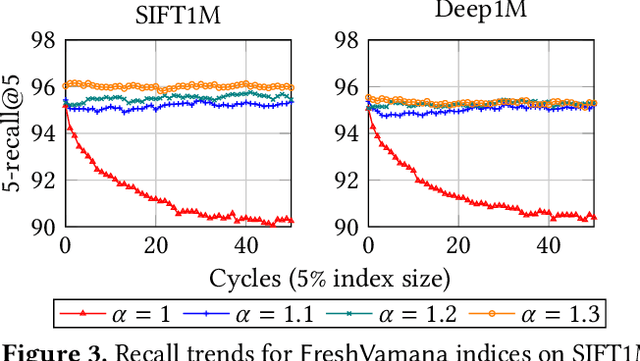
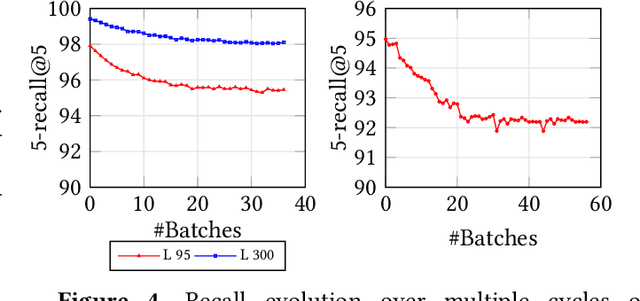
Approximate nearest neighbor search (ANNS) is a fundamental building block in information retrieval with graph-based indices being the current state-of-the-art and widely used in the industry. Recent advances in graph-based indices have made it possible to index and search billion-point datasets with high recall and millisecond-level latency on a single commodity machine with an SSD. However, existing graph algorithms for ANNS support only static indices that cannot reflect real-time changes to the corpus required by many key real-world scenarios (e.g. index of sentences in documents, email, or a news index). To overcome this drawback, the current industry practice for manifesting updates into such indices is to periodically re-build these indices, which can be prohibitively expensive. In this paper, we present the first graph-based ANNS index that reflects corpus updates into the index in real-time without compromising on search performance. Using update rules for this index, we design FreshDiskANN, a system that can index over a billion points on a workstation with an SSD and limited memory, and support thousands of concurrent real-time inserts, deletes and searches per second each, while retaining $>95\%$ 5-recall@5. This represents a 5-10x reduction in the cost of maintaining freshness in indices when compared to existing methods.

Learning Mixture of Gaussians with Streaming Data

In this paper, we study the problem of learning a mixture of Gaussians with streaming data: given a stream of $N$ points in $d$ dimensions generated by an unknown mixture of $k$ spherical Gaussians, the goal is to estimate the model parameters using a single pass over the data stream. We analyze a streaming version of the popular Lloyd's heuristic and show that the algorithm estimates all the unknown centers of the component Gaussians accurately if they are sufficiently separated. Assuming each pair of centers are $C\sigma$ distant with $C=\Omega((k\log k)^{1/4}\sigma)$ and where $\sigma^2$ is the maximum variance of any Gaussian component, we show that asymptotically the algorithm estimates the centers optimally (up to constants); our center separation requirement matches the best known result for spherical Gaussians \citep{vempalawang}. For finite samples, we show that a bias term based on the initial estimate decreases at $O(1/{\rm poly}(N))$ rate while variance decreases at nearly optimal rate of $\sigma^2 d/N$. Our analysis requires seeding the algorithm with a good initial estimate of the true cluster centers for which we provide an online PCA based clustering algorithm. Indeed, the asymptotic per-step time complexity of our algorithm is the optimal $d\cdot k$ while space complexity of our algorithm is $O(dk\log k)$. In addition to the bias and variance terms which tend to $0$, the hard-thresholding based updates of streaming Lloyd's algorithm is agnostic to the data distribution and hence incurs an approximation error that cannot be avoided. However, by using a streaming version of the classical (soft-thresholding-based) EM method that exploits the Gaussian distribution explicitly, we show that for a mixture of two Gaussians the true means can be estimated consistently, with estimation error decreasing at nearly optimal rate, and tending to $0$ for $N\rightarrow \infty$.

Relax, no need to round: integrality of clustering formulations

We study exact recovery conditions for convex relaxations of point cloud clustering problems, focusing on two of the most common optimization problems for unsupervised clustering: $k$-means and $k$-median clustering. Motivations for focusing on convex relaxations are: (a) they come with a certificate of optimality, and (b) they are generic tools which are relatively parameter-free, not tailored to specific assumptions over the input. More precisely, we consider the distributional setting where there are $k$ clusters in $\mathbb{R}^m$ and data from each cluster consists of $n$ points sampled from a symmetric distribution within a ball of unit radius. We ask: what is the minimal separation distance between cluster centers needed for convex relaxations to exactly recover these $k$ clusters as the optimal integral solution? For the $k$-median linear programming relaxation we show a tight bound: exact recovery is obtained given arbitrarily small pairwise separation $\epsilon > 0$ between the balls. In other words, the pairwise center separation is $\Delta > 2+\epsilon$. Under the same distributional model, the $k$-means LP relaxation fails to recover such clusters at separation as large as $\Delta = 4$. Yet, if we enforce PSD constraints on the $k$-means LP, we get exact cluster recovery at center separation $\Delta > 2\sqrt2(1+\sqrt{1/m})$. In contrast, common heuristics such as Lloyd's algorithm (a.k.a. the $k$-means algorithm) can fail to recover clusters in this setting; even with arbitrarily large cluster separation, k-means++ with overseeding by any constant factor fails with high probability at exact cluster recovery. To complement the theoretical analysis, we provide an experimental study of the recovery guarantees for these various methods, and discuss several open problems which these experiments suggest.