DanmakuTPPBench: A Multi-modal Benchmark for Temporal Point Process Modeling and Understanding

We introduce DanmakuTPPBench, a comprehensive benchmark designed to advance multi-modal Temporal Point Process (TPP) modeling in the era of Large Language Models (LLMs). While TPPs have been widely studied for modeling temporal event sequences, existing datasets are predominantly unimodal, hindering progress in models that require joint reasoning over temporal, textual, and visual information. To address this gap, DanmakuTPPBench comprises two complementary components: (1) DanmakuTPP-Events, a novel dataset derived from the Bilibili video platform, where user-generated bullet comments (Danmaku) naturally form multi-modal events annotated with precise timestamps, rich textual content, and corresponding video frames; (2) DanmakuTPP-QA, a challenging question-answering dataset constructed via a novel multi-agent pipeline powered by state-of-the-art LLMs and multi-modal LLMs (MLLMs), targeting complex temporal-textual-visual reasoning. We conduct extensive evaluations using both classical TPP models and recent MLLMs, revealing significant performance gaps and limitations in current methods' ability to model multi-modal event dynamics. Our benchmark establishes strong baselines and calls for further integration of TPP modeling into the multi-modal language modeling landscape. The code and dataset have been released at https://github.com/FRENKIE-CHIANG/DanmakuTPPBench

Grounding 3D Object Affordance with Language Instructions, Visual Observations and Interactions

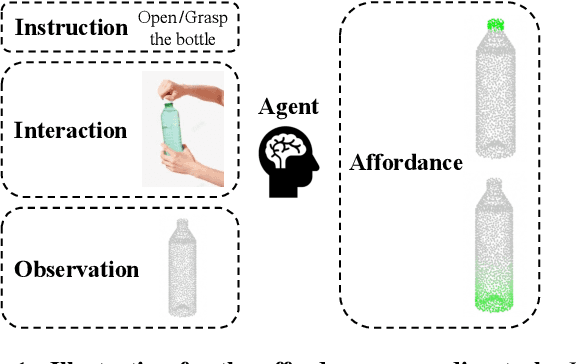
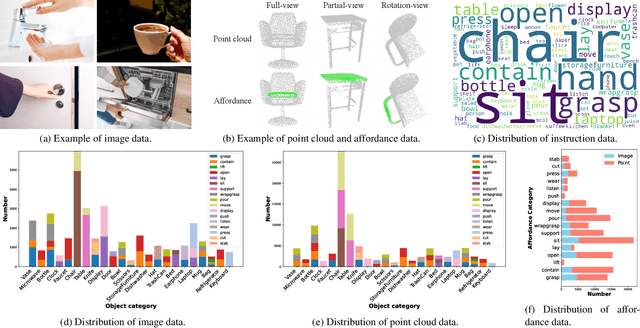
Grounding 3D object affordance is a task that locates objects in 3D space where they can be manipulated, which links perception and action for embodied intelligence. For example, for an intelligent robot, it is necessary to accurately ground the affordance of an object and grasp it according to human instructions. In this paper, we introduce a novel task that grounds 3D object affordance based on language instructions, visual observations and interactions, which is inspired by cognitive science. We collect an Affordance Grounding dataset with Points, Images and Language instructions (AGPIL) to support the proposed task. In the 3D physical world, due to observation orientation, object rotation, or spatial occlusion, we can only get a partial observation of the object. So this dataset includes affordance estimations of objects from full-view, partial-view, and rotation-view perspectives. To accomplish this task, we propose LMAffordance3D, the first multi-modal, language-guided 3D affordance grounding network, which applies a vision-language model to fuse 2D and 3D spatial features with semantic features. Comprehensive experiments on AGPIL demonstrate the effectiveness and superiority of our method on this task, even in unseen experimental settings. Our project is available at https://sites.google.com/view/lmaffordance3d.

Language-TPP: Integrating Temporal Point Processes with Language Models for Event Analysis

Temporal Point Processes (TPPs) have been widely used for event sequence modeling, but they often struggle to incorporate rich textual event descriptions effectively. Conversely, while Large Language Models (LLMs) have been shown remarkable capabilities in processing textual data, they lack mechanisms for handling temporal dynamics. To bridge this gap, we introduce Language-TPP, a unified framework that integrates TPPs with LLMs for enhanced event sequence modeling. Language-TPP introduces a novel temporal encoding mechanism that converts continuous time intervals into specialized byte-tokens, enabling seamless integration with standard LLM architectures. This approach allows Language-TPP to achieve state-of-the-art performance across multiple TPP tasks, including event time prediction, type prediction, and intensity estimation, on five datasets. Additionally, we demonstrate that incorporating temporal information significantly improves the quality of generated event descriptions.

Advances in Temporal Point Processes: Bayesian, Deep, and LLM Approaches

Temporal point processes (TPPs) are stochastic process models used to characterize event sequences occurring in continuous time. Traditional statistical TPPs have a long-standing history, with numerous models proposed and successfully applied across diverse domains. In recent years, advances in deep learning have spurred the development of neural TPPs, enabling greater flexibility and expressiveness in capturing complex temporal dynamics. The emergence of large language models (LLMs) has further sparked excitement, offering new possibilities for modeling and analyzing event sequences by leveraging their rich contextual understanding. This survey presents a comprehensive review of recent research on TPPs from three perspectives: Bayesian, deep learning, and LLM approaches. We begin with a review of the fundamental concepts of TPPs, followed by an in-depth discussion of model design and parameter estimation techniques in these three frameworks. We also revisit classic application areas of TPPs to highlight their practical relevance. Finally, we outline challenges and promising directions for future research.

Integration-free Training for Spatio-temporal Multimodal Covariate Deep Kernel Point Processes

In this study, we propose a novel deep spatio-temporal point process model, Deep Kernel Mixture Point Processes (DKMPP), that incorporates multimodal covariate information. DKMPP is an enhanced version of Deep Mixture Point Processes (DMPP), which uses a more flexible deep kernel to model complex relationships between events and covariate data, improving the model's expressiveness. To address the intractable training procedure of DKMPP due to the non-integrable deep kernel, we utilize an integration-free method based on score matching, and further improve efficiency by adopting a scalable denoising score matching method. Our experiments demonstrate that DKMPP and its corresponding score-based estimators outperform baseline models, showcasing the advantages of incorporating covariate information, utilizing a deep kernel, and employing score-based estimators.

Heterogeneous Multi-Task Gaussian Cox Processes

This paper presents a novel extension of multi-task Gaussian Cox processes for modeling multiple heterogeneous correlated tasks jointly, e.g., classification and regression, via multi-output Gaussian processes (MOGP). A MOGP prior over the parameters of the dedicated likelihoods for classification, regression and point process tasks can facilitate sharing of information between heterogeneous tasks, while allowing for nonparametric parameter estimation. To circumvent the non-conjugate Bayesian inference in the MOGP modulated heterogeneous multi-task framework, we employ the data augmentation technique and derive a mean-field approximation to realize closed-form iterative updates for estimating model parameters. We demonstrate the performance and inference on both 1D synthetic data as well as 2D urban data of Vancouver.

Nonlinear Hawkes Processes in Time-Varying System

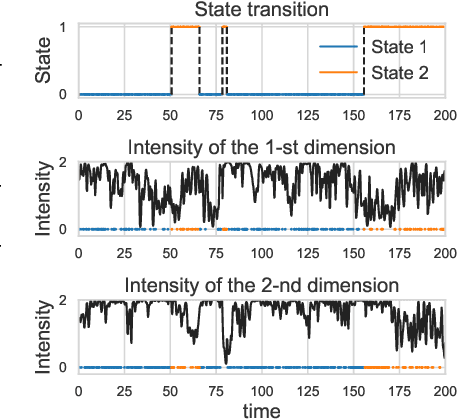
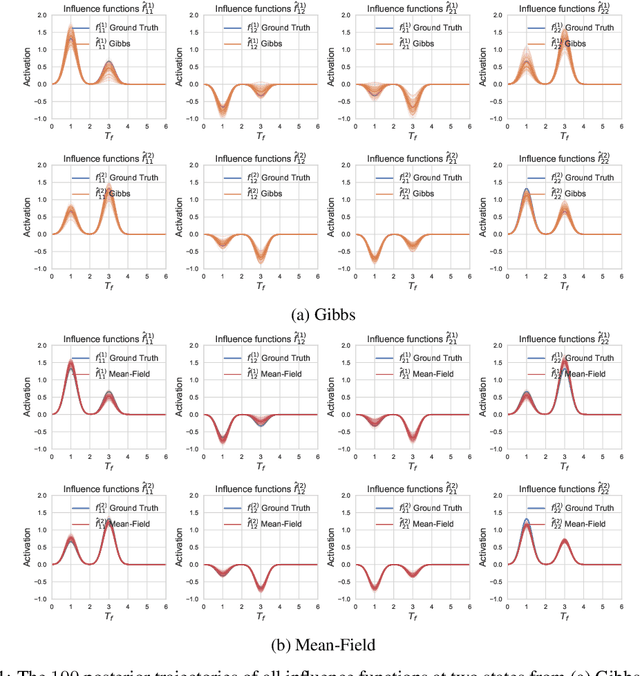
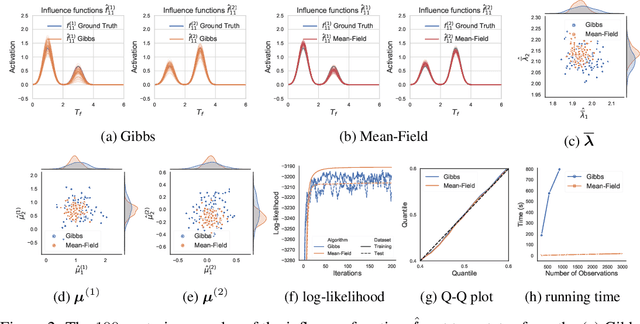
Hawkes processes are a class of point processes that have the ability to model the self- and mutual-exciting phenomena. Although the classic Hawkes processes cover a wide range of applications, their expressive ability is limited due to three key hypotheses: parametric, linear and homogeneous. Recent work has attempted to address these limitations separately. This work aims to overcome all three assumptions simultaneously by proposing the flexible state-switching Hawkes processes: a flexible, nonlinear and nonhomogeneous variant where a state process is incorporated to interact with the point processes. The proposed model empowers Hawkes processes to be applied to time-varying systems. For inference, we utilize the latent variable augmentation technique to design two efficient Bayesian inference algorithms: Gibbs sampler and mean-field variational inference, with analytical iterative updates to estimate the posterior. In experiments, our model achieves superior performance compared to the state-of-the-art competitors.