Boosting Diffusion-Based Text Image Super-Resolution Model Towards Generalized Real-World Scenarios

Restoring low-resolution text images presents a significant challenge, as it requires maintaining both the fidelity and stylistic realism of the text in restored images. Existing text image restoration methods often fall short in hard situations, as the traditional super-resolution models cannot guarantee clarity, while diffusion-based methods fail to maintain fidelity. In this paper, we introduce a novel framework aimed at improving the generalization ability of diffusion models for text image super-resolution (SR), especially promoting fidelity. First, we propose a progressive data sampling strategy that incorporates diverse image types at different stages of training, stabilizing the convergence and improving the generalization. For the network architecture, we leverage a pre-trained SR prior to provide robust spatial reasoning capabilities, enhancing the model's ability to preserve textual information. Additionally, we employ a cross-attention mechanism to better integrate textual priors. To further reduce errors in textual priors, we utilize confidence scores to dynamically adjust the importance of textual features during training. Extensive experiments on real-world datasets demonstrate that our approach not only produces text images with more realistic visual appearances but also improves the accuracy of text structure.

Attributed Graph Clustering in Collaborative Settings

Graph clustering is an unsupervised machine learning method that partitions the nodes in a graph into different groups. Despite achieving significant progress in exploiting both attributed and structured data information, graph clustering methods often face practical challenges related to data isolation. Moreover, the absence of collaborative methods for graph clustering limits their effectiveness. In this paper, we propose a collaborative graph clustering framework for attributed graphs, supporting attributed graph clustering over vertically partitioned data with different participants holding distinct features of the same data. Our method leverages a novel technique that reduces the sample space, improving the efficiency of the attributed graph clustering method. Furthermore, we compare our method to its centralized counterpart under a proximity condition, demonstrating that the successful local results of each participant contribute to the overall success of the collaboration. We fully implement our approach and evaluate its utility and efficiency by conducting experiments on four public datasets. The results demonstrate that our method achieves comparable accuracy levels to centralized attributed graph clustering methods. Our collaborative graph clustering framework provides an efficient and effective solution for graph clustering challenges related to data isolation.

Towards Fair Graph Federated Learning via Incentive Mechanisms

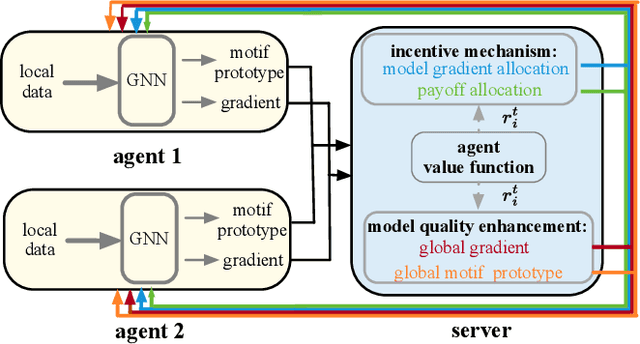
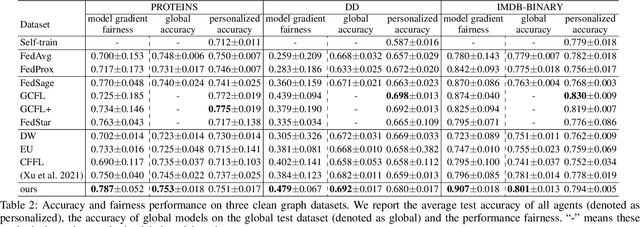
Graph federated learning (FL) has emerged as a pivotal paradigm enabling multiple agents to collaboratively train a graph model while preserving local data privacy. Yet, current efforts overlook a key issue: agents are self-interested and would hesitant to share data without fair and satisfactory incentives. This paper is the first endeavor to address this issue by studying the incentive mechanism for graph federated learning. We identify a unique phenomenon in graph federated learning: the presence of agents posing potential harm to the federation and agents contributing with delays. This stands in contrast to previous FL incentive mechanisms that assume all agents contribute positively and in a timely manner. In view of this, this paper presents a novel incentive mechanism tailored for fair graph federated learning, integrating incentives derived from both model gradient and payoff. To achieve this, we first introduce an agent valuation function aimed at quantifying agent contributions through the introduction of two criteria: gradient alignment and graph diversity. Moreover, due to the high heterogeneity in graph federated learning, striking a balance between accuracy and fairness becomes particularly crucial. We introduce motif prototypes to enhance accuracy, communicated between the server and agents, enhancing global model aggregation and aiding agents in local model optimization. Extensive experiments show that our model achieves the best trade-off between accuracy and the fairness of model gradient, as well as superior payoff fairness.

"Adversarial Examples" for Proof-of-Learning

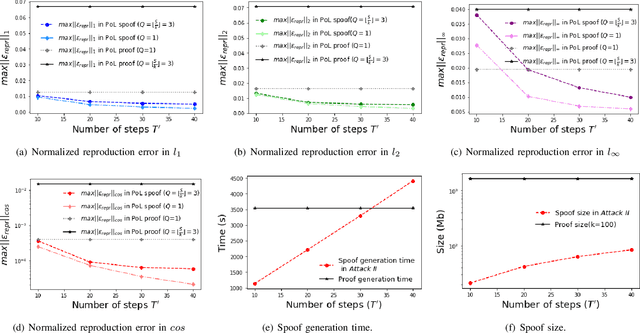
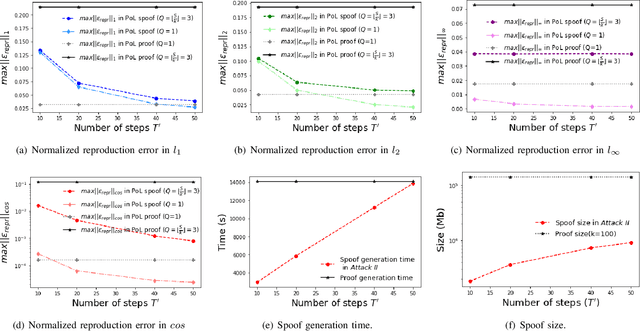
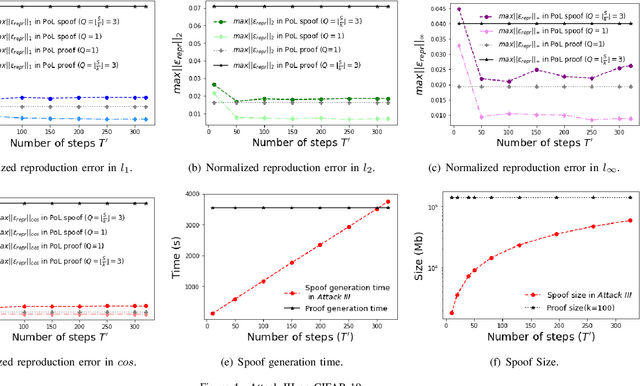
In S&P '21, Jia et al. proposed a new concept/mechanism named proof-of-learning (PoL), which allows a prover to demonstrate ownership of a machine learning model by proving integrity of the training procedure. It guarantees that an adversary cannot construct a valid proof with less cost (in both computation and storage) than that made by the prover in generating the proof. A PoL proof includes a set of intermediate models recorded during training, together with the corresponding data points used to obtain each recorded model. Jia et al. claimed that an adversary merely knowing the final model and training dataset cannot efficiently find a set of intermediate models with correct data points. In this paper, however, we show that PoL is vulnerable to "adversarial examples"! Specifically, in a similar way as optimizing an adversarial example, we could make an arbitrarily-chosen data point "generate" a given model, hence efficiently generating intermediate models with correct data points. We demonstrate, both theoretically and empirically, that we are able to generate a valid proof with significantly less cost than generating a proof by the prover, thereby we successfully break PoL.