"Adversarial Examples" for Proof-of-Learning
Paper and Code
Aug 25, 2021
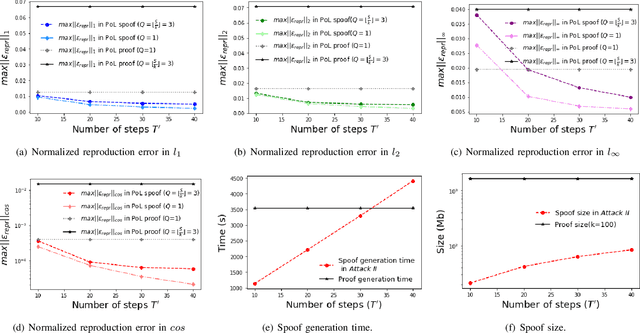
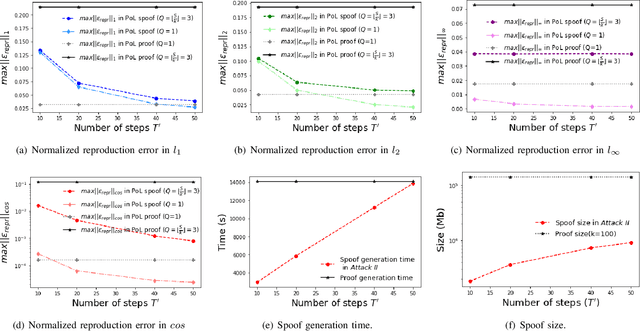
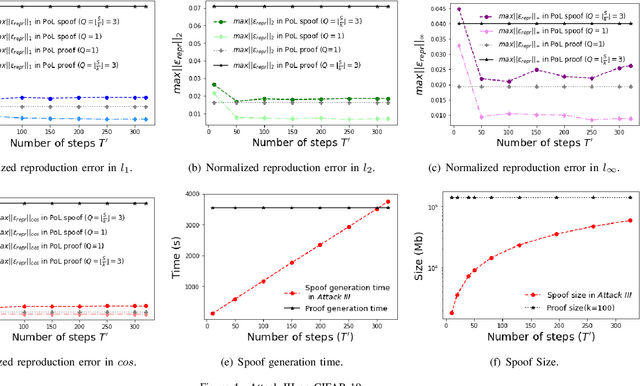
In S&P '21, Jia et al. proposed a new concept/mechanism named proof-of-learning (PoL), which allows a prover to demonstrate ownership of a machine learning model by proving integrity of the training procedure. It guarantees that an adversary cannot construct a valid proof with less cost (in both computation and storage) than that made by the prover in generating the proof. A PoL proof includes a set of intermediate models recorded during training, together with the corresponding data points used to obtain each recorded model. Jia et al. claimed that an adversary merely knowing the final model and training dataset cannot efficiently find a set of intermediate models with correct data points. In this paper, however, we show that PoL is vulnerable to "adversarial examples"! Specifically, in a similar way as optimizing an adversarial example, we could make an arbitrarily-chosen data point "generate" a given model, hence efficiently generating intermediate models with correct data points. We demonstrate, both theoretically and empirically, that we are able to generate a valid proof with significantly less cost than generating a proof by the prover, thereby we successfully break PoL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge