Learning Tree-Structured Composition of Data Augmentation

Data augmentation is widely used for training a neural network given little labeled data. A common practice of augmentation training is applying a composition of multiple transformations sequentially to the data. Existing augmentation methods such as RandAugment randomly sample from a list of pre-selected transformations, while methods such as AutoAugment apply advanced search to optimize over an augmentation set of size $k^d$, which is the number of transformation sequences of length $d$, given a list of $k$ transformations. In this paper, we design efficient algorithms whose running time complexity is much faster than the worst-case complexity of $O(k^d)$, provably. We propose a new algorithm to search for a binary tree-structured composition of $k$ transformations, where each tree node corresponds to one transformation. The binary tree generalizes sequential augmentations, such as the SimCLR augmentation scheme for contrastive learning. Using a top-down, recursive search procedure, our algorithm achieves a runtime complexity of $O(2^d k)$, which is much faster than $O(k^d)$ as $k$ increases above $2$. We apply our algorithm to tackle data distributions with heterogeneous subpopulations by searching for one tree in each subpopulation and then learning a weighted combination, resulting in a forest of trees. We validate our proposed algorithms on numerous graph and image datasets, including a multi-label graph classification dataset we collected. The dataset exhibits significant variations in the sizes of graphs and their average degrees, making it ideal for studying data augmentation. We show that our approach can reduce the computation cost by 43% over existing search methods while improving performance by 4.3%. The tree structures can be used to interpret the relative importance of each transformation, such as identifying the important transformations on small vs. large graphs.

Leveraging Structure for Improved Classification of Grouped Biased Data

We consider semi-supervised binary classification for applications in which data points are naturally grouped (e.g., survey responses grouped by state) and the labeled data is biased (e.g., survey respondents are not representative of the population). The groups overlap in the feature space and consequently the input-output patterns are related across the groups. To model the inherent structure in such data, we assume the partition-projected class-conditional invariance across groups, defined in terms of the group-agnostic feature space. We demonstrate that under this assumption, the group carries additional information about the class, over the group-agnostic features, with provably improved area under the ROC curve. Further assuming invariance of partition-projected class-conditional distributions across both labeled and unlabeled data, we derive a semi-supervised algorithm that explicitly leverages the structure to learn an optimal, group-aware, probability-calibrated classifier, despite the bias in the labeled data. Experiments on synthetic and real data demonstrate the efficacy of our algorithm over suitable baselines and ablative models, spanning standard supervised and semi-supervised learning approaches, with and without incorporating the group directly as a feature.

Explaining Deep Tractable Probabilistic Models: The sum-product network case

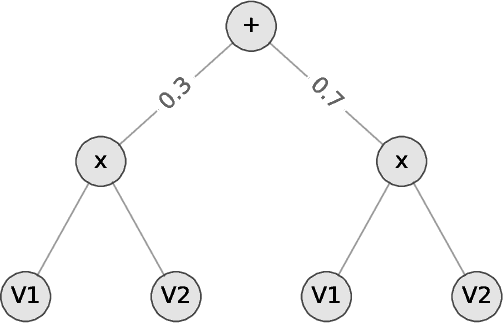
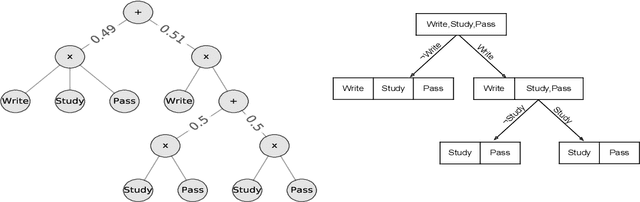
We consider the problem of explaining a tractable deep probabilistic model, the Sum-Product Networks (SPNs).To this effect, we define the notion of a context-specific independence tree and present an iterative algorithm that converts an SPN to a CSI-tree. The resulting CSI-tree is both interpretable and explainable to the domain expert. To further compress the tree, we approximate the CSIs by fitting a supervised classifier. Our extensive empirical evaluations on synthetic, standard, and real-world clinical data sets demonstrate that the resulting models exhibit superior explainability without loss in performance.

A new class of metrics for learning on real-valued and structured data

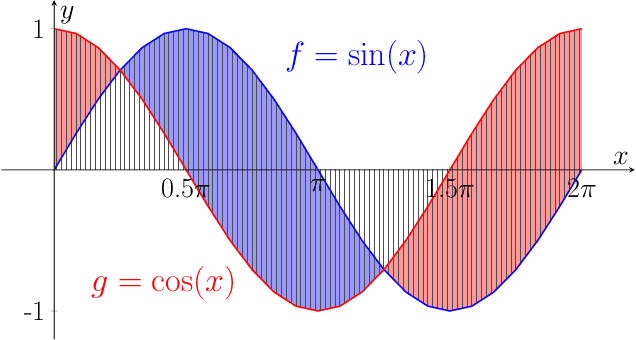
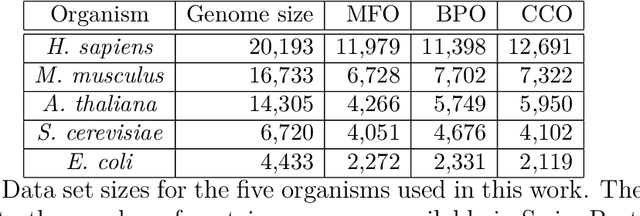
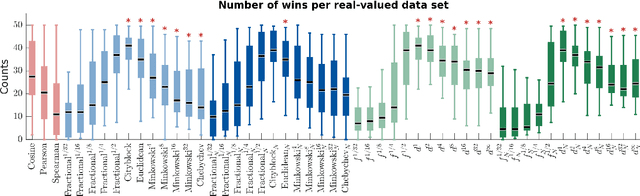
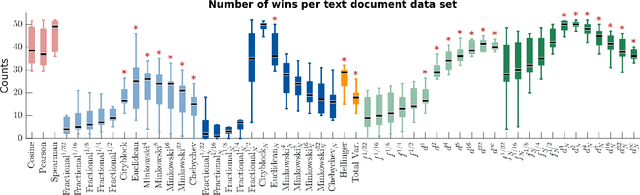
We propose a new class of metrics on sets, vectors, and functions that can be used in various stages of data mining, including exploratory data analysis, learning, and result interpretation. These new distance functions unify and generalize some of the popular metrics, such as the Jaccard and bag distances on sets, Manhattan distance on vector spaces, and Marczewski-Steinhaus distance on integrable functions. We prove that the new metrics are complete and show useful relationships with $f$-divergences for probability distributions. To further extend our approach to structured objects such as concept hierarchies and ontologies, we introduce information-theoretic metrics on directed acyclic graphs drawn according to a fixed probability distribution. We conduct empirical investigation to demonstrate intuitive interpretation of the new metrics and their effectiveness on real-valued, high-dimensional, and structured data. Extensive comparative evaluation demonstrates that the new metrics outperformed multiple similarity and dissimilarity functions traditionally used in data mining, including the Minkowski family, the fractional $L^p$ family, two $f$-divergences, cosine distance, and two correlation coefficients. Finally, we argue that the new class of metrics is particularly appropriate for rapid processing of high-dimensional and structured data in distance-based learning.

Classification in biological networks with hypergraphlet kernels

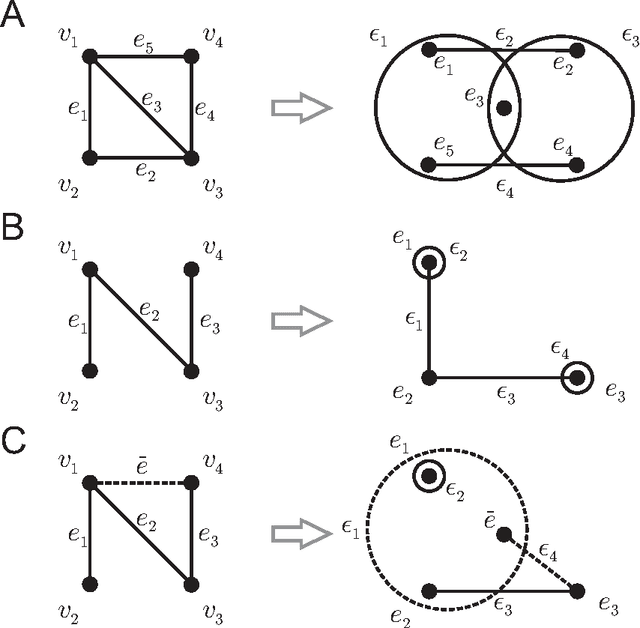
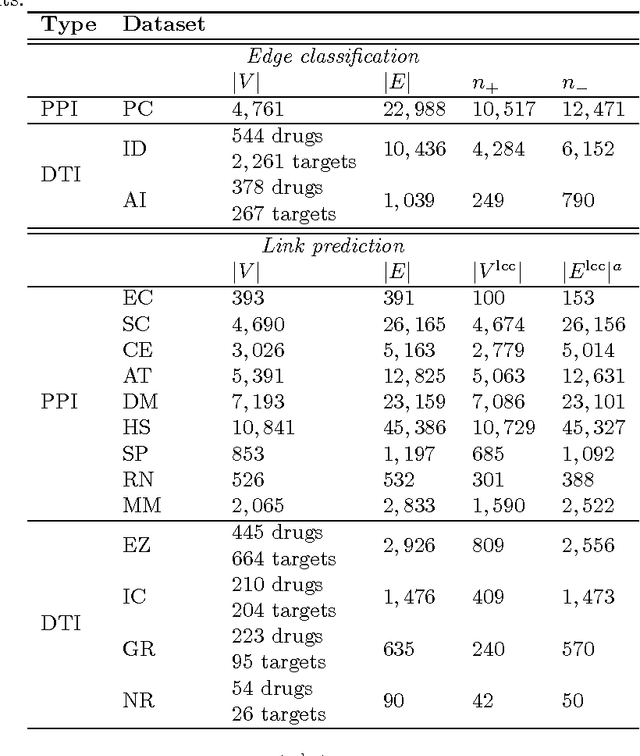
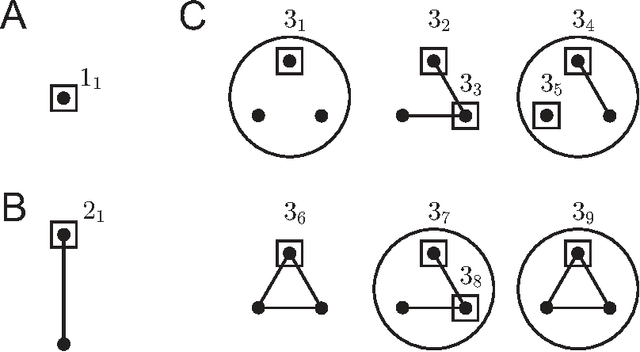
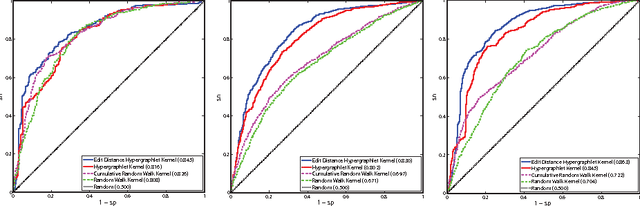
Biological and cellular systems are often modeled as graphs in which vertices represent objects of interest (genes, proteins, drugs) and edges represent relational ties among these objects (binds-to, interacts-with, regulates). This approach has been highly successful owing to the theory, methodology and software that support analysis and learning on graphs. Graphs, however, often suffer from information loss when modeling physical systems due to their inability to accurately represent multiobject relationships. Hypergraphs, a generalization of graphs, provide a framework to mitigate information loss and unify disparate graph-based methodologies. In this paper, we present a hypergraph-based approach for modeling physical systems and formulate vertex classification, edge classification and link prediction problems on (hyper)graphs as instances of vertex classification on (extended, dual) hypergraphs in a semi-supervised setting. We introduce a novel kernel method on vertex- and edge-labeled (colored) hypergraphs for analysis and learning. The method is based on exact and inexact (via hypergraph edit distances) enumeration of small simple hypergraphs, referred to as hypergraphlets, rooted at a vertex of interest. We extensively evaluate this method and show its potential use in a positive-unlabeled setting to estimate the number of missing and false positive links in protein-protein interaction networks.

Recovering True Classifier Performance in Positive-Unlabeled Learning

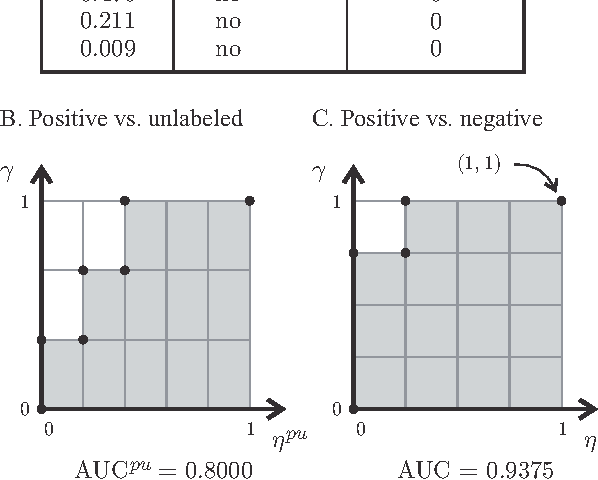
A common approach in positive-unlabeled learning is to train a classification model between labeled and unlabeled data. This strategy is in fact known to give an optimal classifier under mild conditions; however, it results in biased empirical estimates of the classifier performance. In this work, we show that the typically used performance measures such as the receiver operating characteristic curve, or the precision-recall curve obtained on such data can be corrected with the knowledge of class priors; i.e., the proportions of the positive and negative examples in the unlabeled data. We extend the results to a noisy setting where some of the examples labeled positive are in fact negative and show that the correction also requires the knowledge of the proportion of noisy examples in the labeled positives. Using state-of-the-art algorithms to estimate the positive class prior and the proportion of noise, we experimentally evaluate two correction approaches and demonstrate their efficacy on real-life data.

Estimating the class prior and posterior from noisy positives and unlabeled data

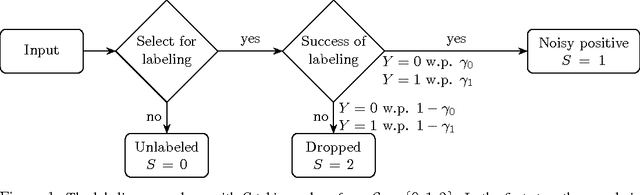
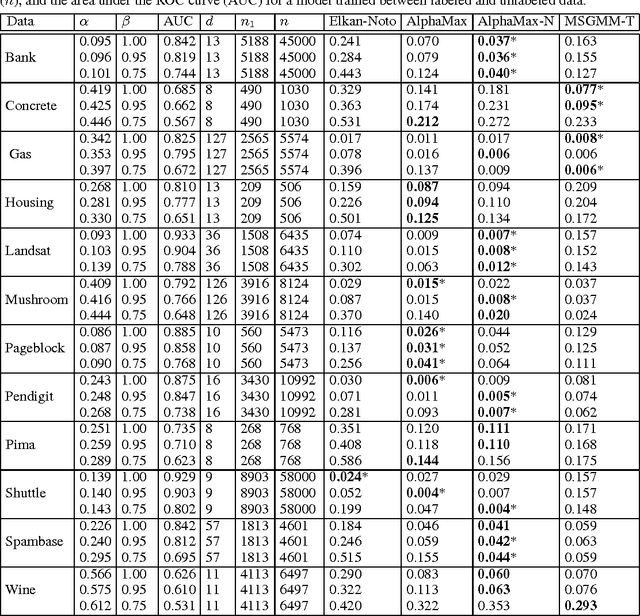
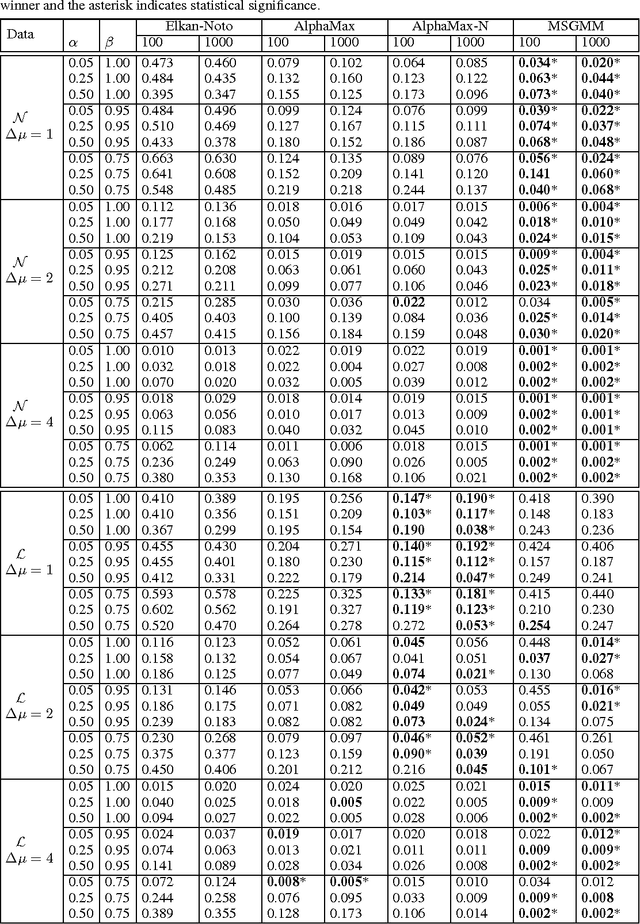
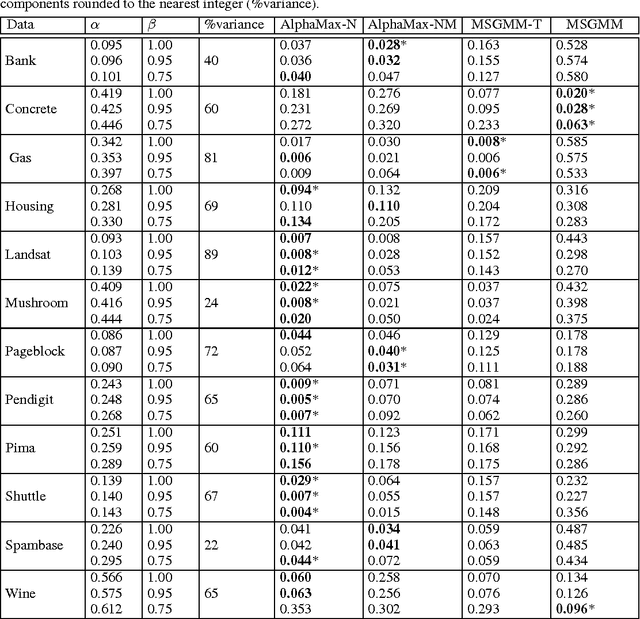
We develop a classification algorithm for estimating posterior distributions from positive-unlabeled data, that is robust to noise in the positive labels and effective for high-dimensional data. In recent years, several algorithms have been proposed to learn from positive-unlabeled data; however, many of these contributions remain theoretical, performing poorly on real high-dimensional data that is typically contaminated with noise. We build on this previous work to develop two practical classification algorithms that explicitly model the noise in the positive labels and utilize univariate transforms built on discriminative classifiers. We prove that these univariate transforms preserve the class prior, enabling estimation in the univariate space and avoiding kernel density estimation for high-dimensional data. The theoretical development and both parametric and nonparametric algorithms proposed here constitutes an important step towards wide-spread use of robust classification algorithms for positive-unlabeled data.

Ultra High-Dimensional Nonlinear Feature Selection for Big Biological Data

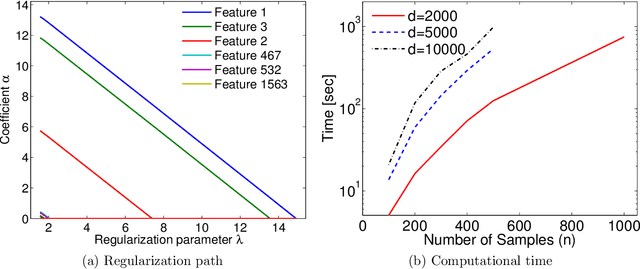
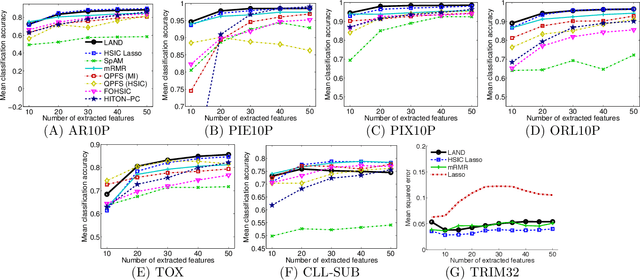
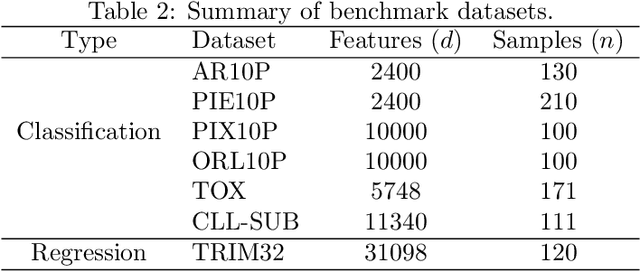
Machine learning methods are used to discover complex nonlinear relationships in biological and medical data. However, sophisticated learning models are computationally unfeasible for data with millions of features. Here we introduce the first feature selection method for nonlinear learning problems that can scale up to large, ultra-high dimensional biological data. More specifically, we scale up the novel Hilbert-Schmidt Independence Criterion Lasso (HSIC Lasso) to handle millions of features with tens of thousand samples. The proposed method is guaranteed to find an optimal subset of maximally predictive features with minimal redundancy, yielding higher predictive power and improved interpretability. Its effectiveness is demonstrated through applications to classify phenotypes based on module expression in human prostate cancer patients and to detect enzymes among protein structures. We achieve high accuracy with as few as 20 out of one million features --- a dimensionality reduction of 99.998%. Our algorithm can be implemented on commodity cloud computing platforms. The dramatic reduction of features may lead to the ubiquitous deployment of sophisticated prediction models in mobile health care applications.

Nonparametric semi-supervised learning of class proportions

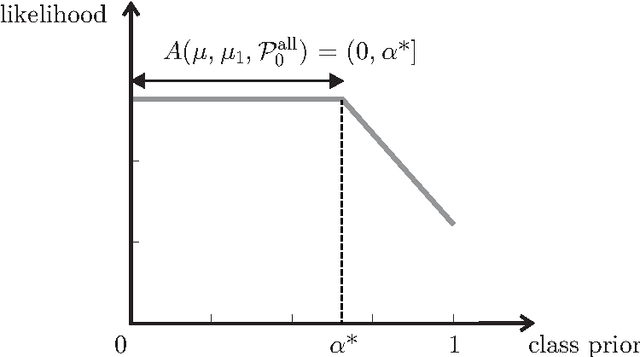
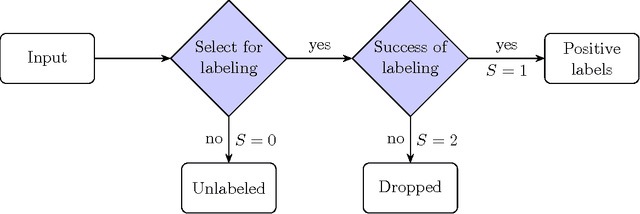
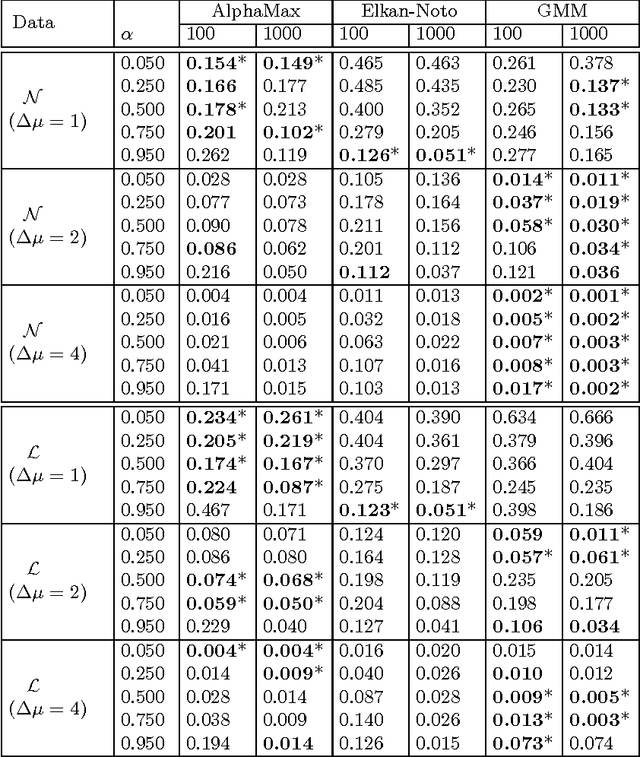
The problem of developing binary classifiers from positive and unlabeled data is often encountered in machine learning. A common requirement in this setting is to approximate posterior probabilities of positive and negative classes for a previously unseen data point. This problem can be decomposed into two steps: (i) the development of accurate predictors that discriminate between positive and unlabeled data, and (ii) the accurate estimation of the prior probabilities of positive and negative examples. In this work we primarily focus on the latter subproblem. We study nonparametric class prior estimation and formulate this problem as an estimation of mixing proportions in two-component mixture models, given a sample from one of the components and another sample from the mixture itself. We show that estimation of mixing proportions is generally ill-defined and propose a canonical form to obtain identifiability while maintaining the flexibility to model any distribution. We use insights from this theory to elucidate the optimization surface of the class priors and propose an algorithm for estimating them. To address the problems of high-dimensional density estimation, we provide practical transformations to low-dimensional spaces that preserve class priors. Finally, we demonstrate the efficacy of our method on univariate and multivariate data.

Uncovering protein interaction in abstracts and text using a novel linear model and word proximity networks

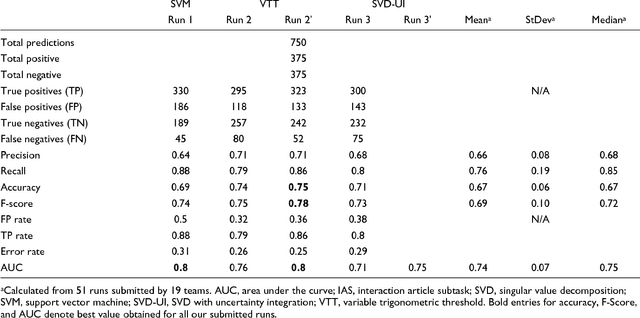
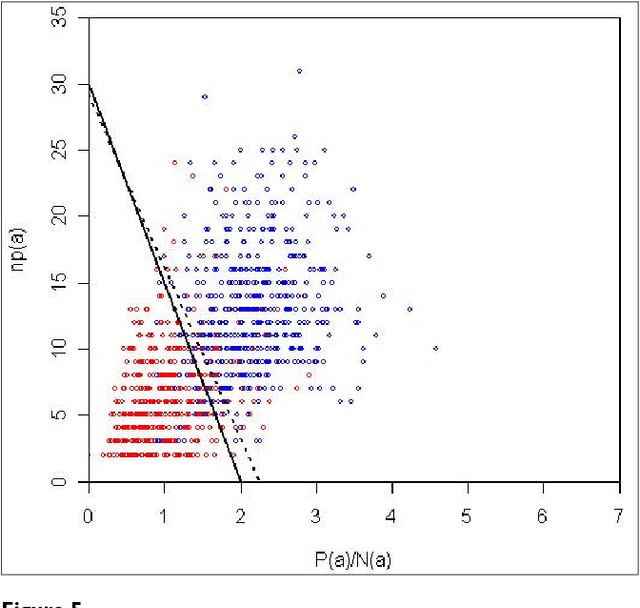
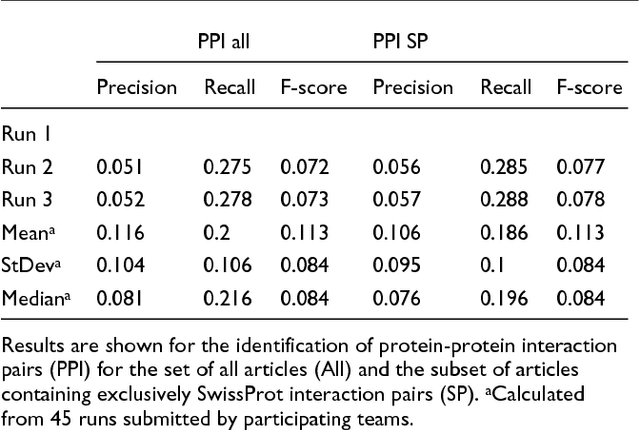
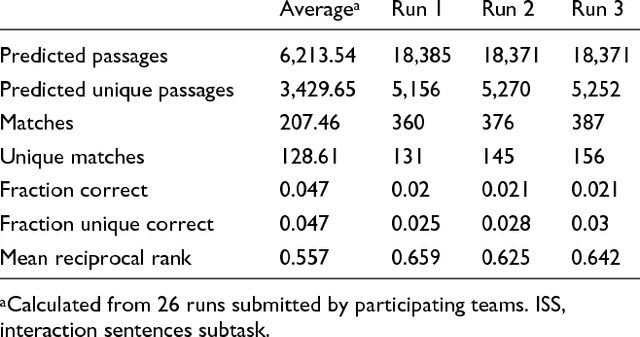
We participated in three of the protein-protein interaction subtasks of the Second BioCreative Challenge: classification of abstracts relevant for protein-protein interaction (IAS), discovery of protein pairs (IPS) and text passages characterizing protein interaction (ISS) in full text documents. We approached the abstract classification task with a novel, lightweight linear model inspired by spam-detection techniques, as well as an uncertainty-based integration scheme. We also used a Support Vector Machine and the Singular Value Decomposition on the same features for comparison purposes. Our approach to the full text subtasks (protein pair and passage identification) includes a feature expansion method based on word-proximity networks. Our approach to the abstract classification task (IAS) was among the top submissions for this task in terms of the measures of performance used in the challenge evaluation (accuracy, F-score and AUC). We also report on a web-tool we produced using our approach: the Protein Interaction Abstract Relevance Evaluator (PIARE). Our approach to the full text tasks resulted in one of the highest recall rates as well as mean reciprocal rank of correct passages. Our approach to abstract classification shows that a simple linear model, using relatively few features, is capable of generalizing and uncovering the conceptual nature of protein-protein interaction from the bibliome. Since the novel approach is based on a very lightweight linear model, it can be easily ported and applied to similar problems. In full text problems, the expansion of word features with word-proximity networks is shown to be useful, though the need for some improvements is discussed.