Avishek Saha
MBA: Mini-Batch AUC Optimization
May 31, 2018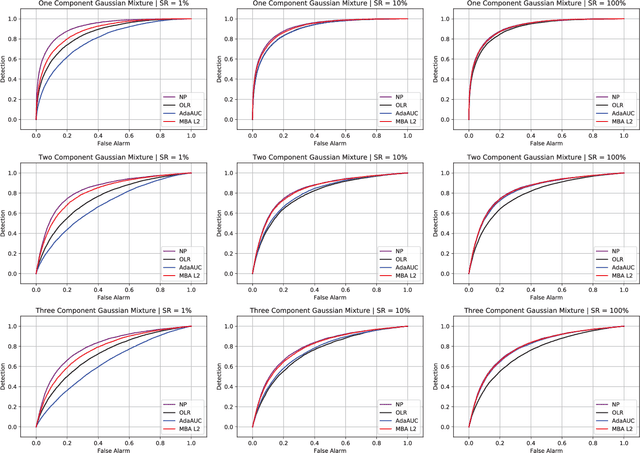
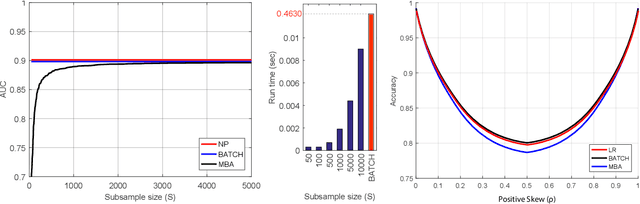
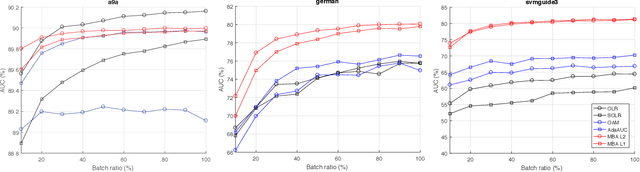
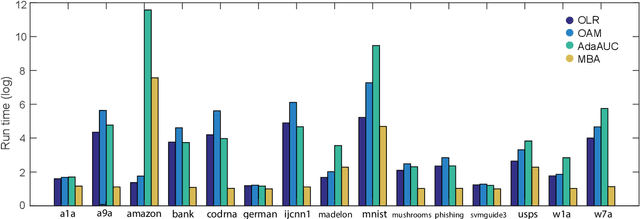
Abstract:Area under the receiver operating characteristics curve (AUC) is an important metric for a wide range of signal processing and machine learning problems, and scalable methods for optimizing AUC have recently been proposed. However, handling very large datasets remains an open challenge for this problem. This paper proposes a novel approach to AUC maximization, based on sampling mini-batches of positive/negative instance pairs and computing U-statistics to approximate a global risk minimization problem. The resulting algorithm is simple, fast, and learning-rate free. We show that the number of samples required for good performance is independent of the number of pairs available, which is a quadratic function of the positive and negative instances. Extensive experiments show the practical utility of the proposed method.
Ultra High-Dimensional Nonlinear Feature Selection for Big Biological Data
Aug 14, 2016
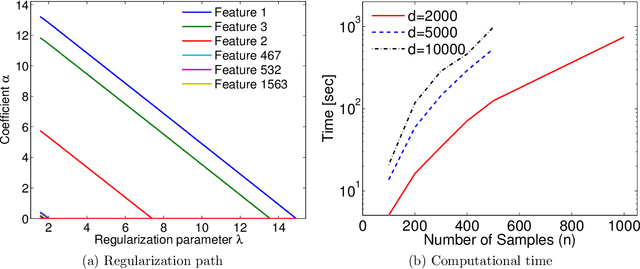
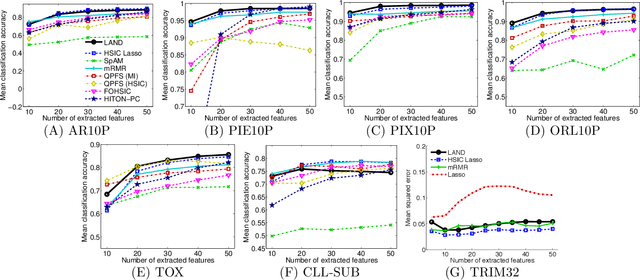
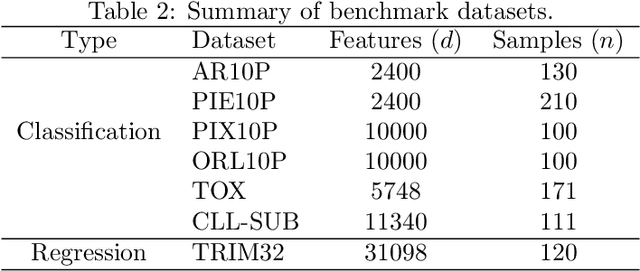
Abstract:Machine learning methods are used to discover complex nonlinear relationships in biological and medical data. However, sophisticated learning models are computationally unfeasible for data with millions of features. Here we introduce the first feature selection method for nonlinear learning problems that can scale up to large, ultra-high dimensional biological data. More specifically, we scale up the novel Hilbert-Schmidt Independence Criterion Lasso (HSIC Lasso) to handle millions of features with tens of thousand samples. The proposed method is guaranteed to find an optimal subset of maximally predictive features with minimal redundancy, yielding higher predictive power and improved interpretability. Its effectiveness is demonstrated through applications to classify phenotypes based on module expression in human prostate cancer patients and to detect enzymes among protein structures. We achieve high accuracy with as few as 20 out of one million features --- a dimensionality reduction of 99.998%. Our algorithm can be implemented on commodity cloud computing platforms. The dramatic reduction of features may lead to the ubiquitous deployment of sophisticated prediction models in mobile health care applications.
N$^3$LARS: Minimum Redundancy Maximum Relevance Feature Selection for Large and High-dimensional Data
Nov 10, 2014



Abstract:We propose a feature selection method that finds non-redundant features from a large and high-dimensional data in nonlinear way. Specifically, we propose a nonlinear extension of the non-negative least-angle regression (LARS) called N${}^3$LARS, where the similarity between input and output is measured through the normalized version of the Hilbert-Schmidt Independence Criterion (HSIC). An advantage of N${}^3$LARS is that it can easily incorporate with map-reduce frameworks such as Hadoop and Spark. Thus, with the help of distributed computing, a set of features can be efficiently selected from a large and high-dimensional data. Moreover, N${}^3$LARS is a convex method and can find a global optimum solution. The effectiveness of the proposed method is first demonstrated through feature selection experiments for classification and regression with small and high-dimensional datasets. Finally, we evaluate our proposed method over a large and high-dimensional biology dataset.
A Geometric Algorithm for Scalable Multiple Kernel Learning
Mar 15, 2014


Abstract:We present a geometric formulation of the Multiple Kernel Learning (MKL) problem. To do so, we reinterpret the problem of learning kernel weights as searching for a kernel that maximizes the minimum (kernel) distance between two convex polytopes. This interpretation combined with novel structural insights from our geometric formulation allows us to reduce the MKL problem to a simple optimization routine that yields provable convergence as well as quality guarantees. As a result our method scales efficiently to much larger data sets than most prior methods can handle. Empirical evaluation on eleven datasets shows that we are significantly faster and even compare favorably with a uniform unweighted combination of kernels.
Efficient Protocols for Distributed Classification and Optimization
Apr 16, 2012



Abstract:In distributed learning, the goal is to perform a learning task over data distributed across multiple nodes with minimal (expensive) communication. Prior work (Daume III et al., 2012) proposes a general model that bounds the communication required for learning classifiers while allowing for $\eps$ training error on linearly separable data adversarially distributed across nodes. In this work, we develop key improvements and extensions to this basic model. Our first result is a two-party multiplicative-weight-update based protocol that uses $O(d^2 \log{1/\eps})$ words of communication to classify distributed data in arbitrary dimension $d$, $\eps$-optimally. This readily extends to classification over $k$ nodes with $O(kd^2 \log{1/\eps})$ words of communication. Our proposed protocol is simple to implement and is considerably more efficient than baselines compared, as demonstrated by our empirical results. In addition, we illustrate general algorithm design paradigms for doing efficient learning over distributed data. We show how to solve fixed-dimensional and high dimensional linear programming efficiently in a distributed setting where constraints may be distributed across nodes. Since many learning problems can be viewed as convex optimization problems where constraints are generated by individual points, this models many typical distributed learning scenarios. Our techniques make use of a novel connection from multipass streaming, as well as adapting the multiplicative-weight-update framework more generally to a distributed setting. As a consequence, our methods extend to the wide range of problems solvable using these techniques.
Protocols for Learning Classifiers on Distributed Data
Feb 27, 2012



Abstract:We consider the problem of learning classifiers for labeled data that has been distributed across several nodes. Our goal is to find a single classifier, with small approximation error, across all datasets while minimizing the communication between nodes. This setting models real-world communication bottlenecks in the processing of massive distributed datasets. We present several very general sampling-based solutions as well as some two-way protocols which have a provable exponential speed-up over any one-way protocol. We focus on core problems for noiseless data distributed across two or more nodes. The techniques we introduce are reminiscent of active learning, but rather than actively probing labels, nodes actively communicate with each other, each node simultaneously learning the important data from another node.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge