A Geometric Algorithm for Scalable Multiple Kernel Learning

We present a geometric formulation of the Multiple Kernel Learning (MKL) problem. To do so, we reinterpret the problem of learning kernel weights as searching for a kernel that maximizes the minimum (kernel) distance between two convex polytopes. This interpretation combined with novel structural insights from our geometric formulation allows us to reduce the MKL problem to a simple optimization routine that yields provable convergence as well as quality guarantees. As a result our method scales efficiently to much larger data sets than most prior methods can handle. Empirical evaluation on eleven datasets shows that we are significantly faster and even compare favorably with a uniform unweighted combination of kernels.

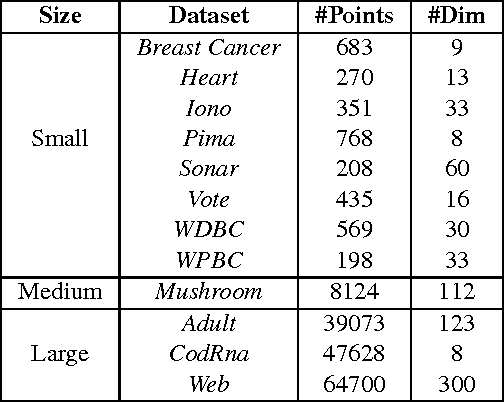
Power to the Points: Validating Data Memberships in Clusterings

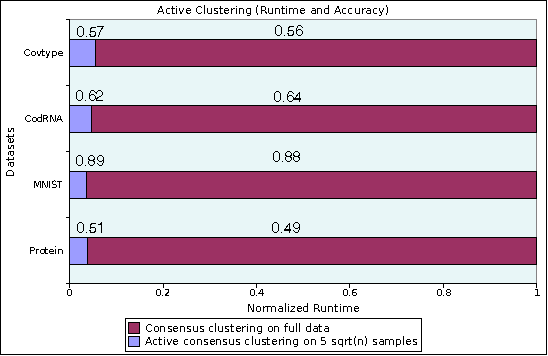
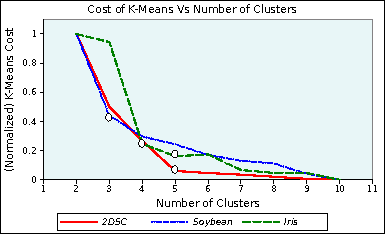
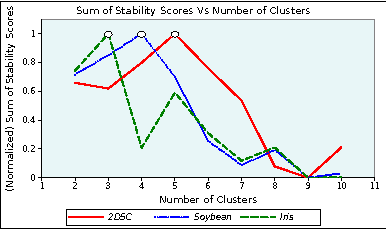
A clustering is an implicit assignment of labels of points, based on proximity to other points. It is these labels that are then used for downstream analysis (either focusing on individual clusters, or identifying representatives of clusters and so on). Thus, in order to trust a clustering as a first step in exploratory data analysis, we must trust the labels assigned to individual data. Without supervision, how can we validate this assignment? In this paper, we present a method to attach affinity scores to the implicit labels of individual points in a clustering. The affinity scores capture the confidence level of the cluster that claims to "own" the point. This method is very general: it can be used with clusterings derived from Euclidean data, kernelized data, or even data derived from information spaces. It smoothly incorporates importance functions on clusters, allowing us to eight different clusters differently. It is also efficient: assigning an affinity score to a point depends only polynomially on the number of clusters and is independent of the number of points in the data. The dimensionality of the underlying space only appears in preprocessing. We demonstrate the value of our approach with an experimental study that illustrates the use of these scores in different data analysis tasks, as well as the efficiency and flexibility of the method. We also demonstrate useful visualizations of these scores; these might prove useful within an interactive analytics framework.

Generating a Diverse Set of High-Quality Clusterings

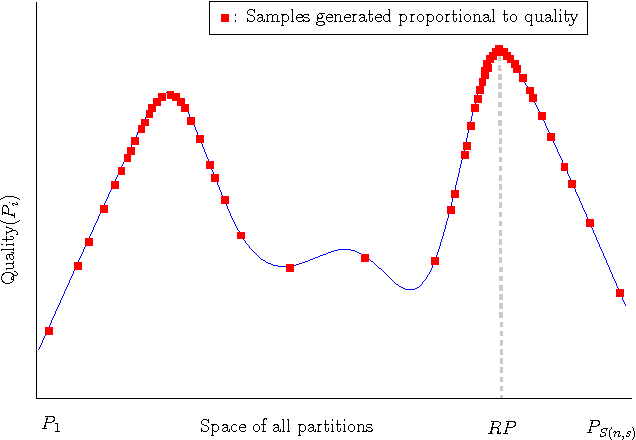
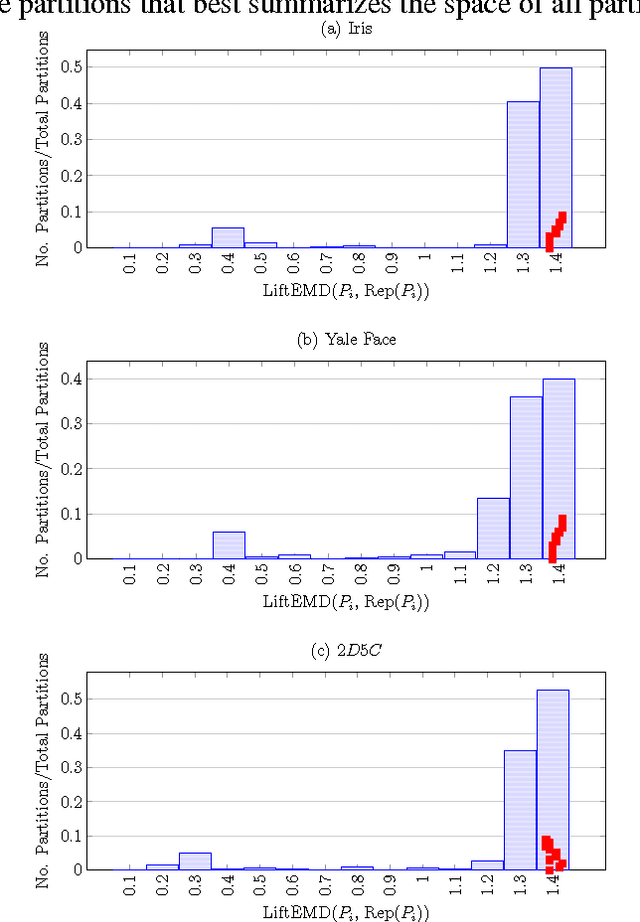
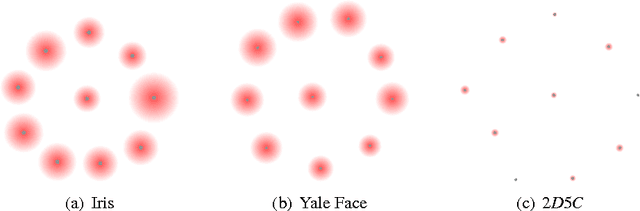
We provide a new framework for generating multiple good quality partitions (clusterings) of a single data set. Our approach decomposes this problem into two components, generating many high-quality partitions, and then grouping these partitions to obtain k representatives. The decomposition makes the approach extremely modular and allows us to optimize various criteria that control the choice of representative partitions.

Spatially-Aware Comparison and Consensus for Clusterings

This paper proposes a new distance metric between clusterings that incorporates information about the spatial distribution of points and clusters. Our approach builds on the idea of a Hilbert space-based representation of clusters as a combination of the representations of their constituent points. We use this representation and the underlying metric to design a spatially-aware consensus clustering procedure. This consensus procedure is implemented via a novel reduction to Euclidean clustering, and is both simple and efficient. All of our results apply to both soft and hard clusterings. We accompany these algorithms with a detailed experimental evaluation that demonstrates the efficiency and quality of our techniques.