A Unified View of Localized Kernel Learning

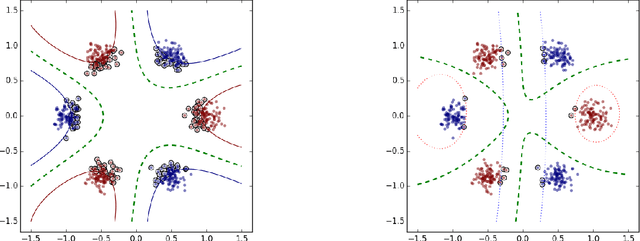
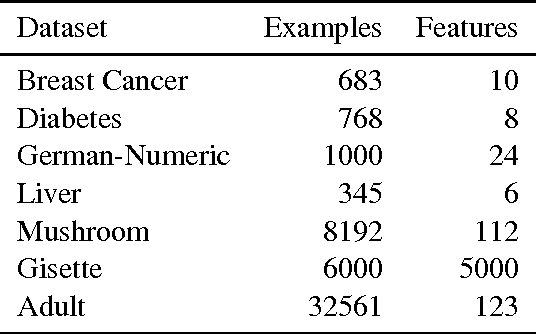
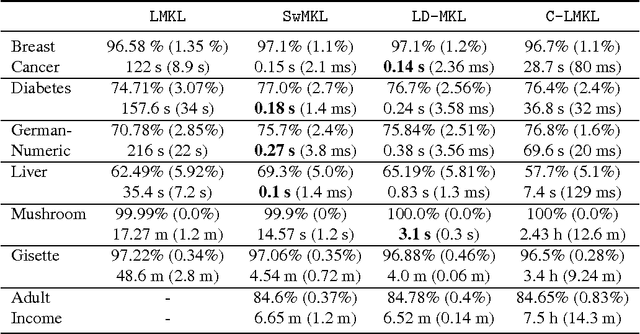
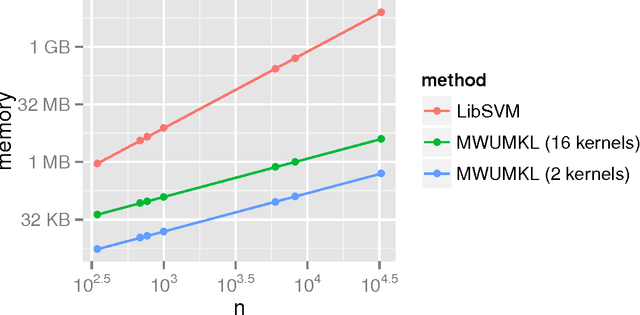
Multiple Kernel Learning, or MKL, extends (kernelized) SVM by attempting to learn not only a classifier/regressor but also the best kernel for the training task, usually from a combination of existing kernel functions. Most MKL methods seek the combined kernel that performs best over every training example, sacrificing performance in some areas to seek a global optimum. Localized kernel learning (LKL) overcomes this limitation by allowing the training algorithm to match a component kernel to the examples that can exploit it best. Several approaches to the localized kernel learning problem have been explored in the last several years. We unify many of these approaches under one simple system and design a new algorithm with improved performance. We also develop enhanced versions of existing algorithms, with an eye on scalability and performance.

Certifying and removing disparate impact

What does it mean for an algorithm to be biased? In U.S. law, unintentional bias is encoded via disparate impact, which occurs when a selection process has widely different outcomes for different groups, even as it appears to be neutral. This legal determination hinges on a definition of a protected class (ethnicity, gender, religious practice) and an explicit description of the process. When the process is implemented using computers, determining disparate impact (and hence bias) is harder. It might not be possible to disclose the process. In addition, even if the process is open, it might be hard to elucidate in a legal setting how the algorithm makes its decisions. Instead of requiring access to the algorithm, we propose making inferences based on the data the algorithm uses. We make four contributions to this problem. First, we link the legal notion of disparate impact to a measure of classification accuracy that while known, has received relatively little attention. Second, we propose a test for disparate impact based on analyzing the information leakage of the protected class from the other data attributes. Third, we describe methods by which data might be made unbiased. Finally, we present empirical evidence supporting the effectiveness of our test for disparate impact and our approach for both masking bias and preserving relevant information in the data. Interestingly, our approach resembles some actual selection practices that have recently received legal scrutiny.

A Geometric Algorithm for Scalable Multiple Kernel Learning

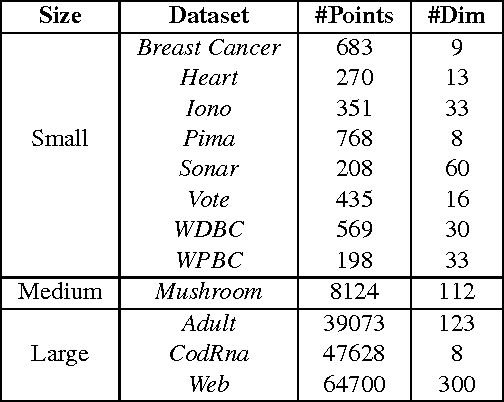
We present a geometric formulation of the Multiple Kernel Learning (MKL) problem. To do so, we reinterpret the problem of learning kernel weights as searching for a kernel that maximizes the minimum (kernel) distance between two convex polytopes. This interpretation combined with novel structural insights from our geometric formulation allows us to reduce the MKL problem to a simple optimization routine that yields provable convergence as well as quality guarantees. As a result our method scales efficiently to much larger data sets than most prior methods can handle. Empirical evaluation on eleven datasets shows that we are significantly faster and even compare favorably with a uniform unweighted combination of kernels.