A Geometric Algorithm for Scalable Multiple Kernel Learning
Paper and Code
Mar 15, 2014
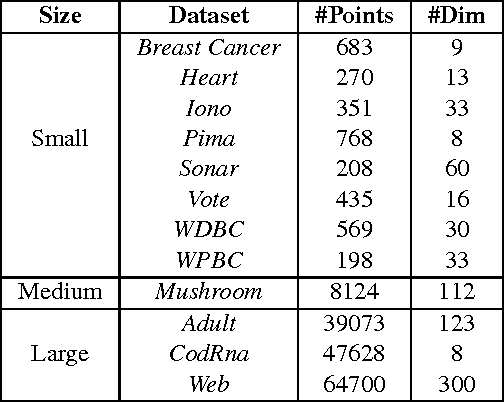


We present a geometric formulation of the Multiple Kernel Learning (MKL) problem. To do so, we reinterpret the problem of learning kernel weights as searching for a kernel that maximizes the minimum (kernel) distance between two convex polytopes. This interpretation combined with novel structural insights from our geometric formulation allows us to reduce the MKL problem to a simple optimization routine that yields provable convergence as well as quality guarantees. As a result our method scales efficiently to much larger data sets than most prior methods can handle. Empirical evaluation on eleven datasets shows that we are significantly faster and even compare favorably with a uniform unweighted combination of kernels.
* 20 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge