San Gultekin
Nonlinear Kalman Filtering with Reparametrization Gradients
Mar 08, 2023

Abstract:We introduce a novel nonlinear Kalman filter that utilizes reparametrization gradients. The widely used parametric approximation is based on a jointly Gaussian assumption of the state-space model, which is in turn equivalent to minimizing an approximation to the Kullback-Leibler divergence. It is possible to obtain better approximations using the alpha divergence, but the resulting problem is substantially more complex. In this paper, we introduce an alternate formulation based on an energy function, which can be optimized instead of the alpha divergence. The optimization can be carried out using reparametrization gradients, a technique that has recently been utilized in a number of deep learning models.
An Efficient Deep Distribution Network for Bid Shading in First-Price Auctions
Jul 15, 2021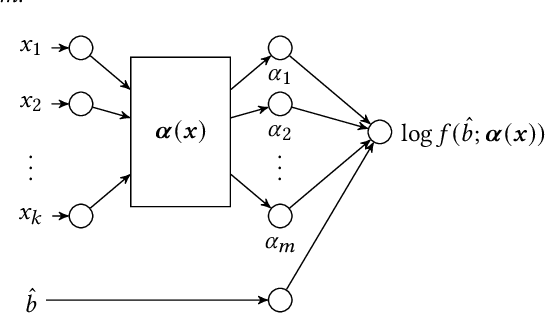
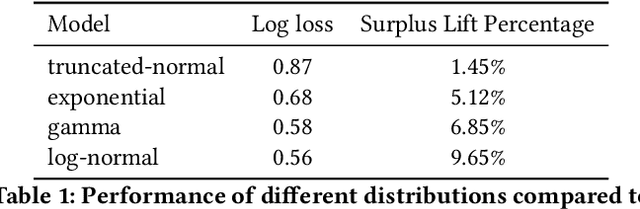
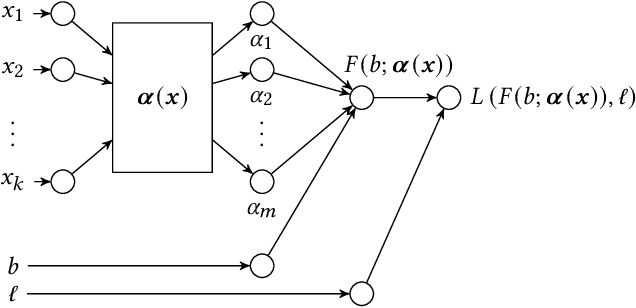
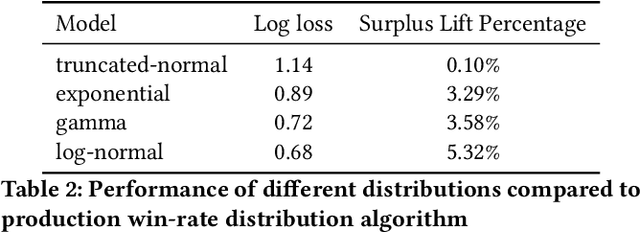
Abstract:Since 2019, most ad exchanges and sell-side platforms (SSPs), in the online advertising industry, shifted from second to first price auctions. Due to the fundamental difference between these auctions, demand-side platforms (DSPs) have had to update their bidding strategies to avoid bidding unnecessarily high and hence overpaying. Bid shading was proposed to adjust the bid price intended for second-price auctions, in order to balance cost and winning probability in a first-price auction setup. In this study, we introduce a novel deep distribution network for optimal bidding in both open (non-censored) and closed (censored) online first-price auctions. Offline and online A/B testing results show that our algorithm outperforms previous state-of-art algorithms in terms of both surplus and effective cost per action (eCPX) metrics. Furthermore, the algorithm is optimized in run-time and has been deployed into VerizonMedia DSP as production algorithm, serving hundreds of billions of bid requests per day. Online A/B test shows that advertiser's ROI are improved by +2.4%, +2.4%, and +8.6% for impression based (CPM), click based (CPC), and conversion based (CPA) campaigns respectively.
Bid Shading by Win-Rate Estimation and Surplus Maximization
Sep 19, 2020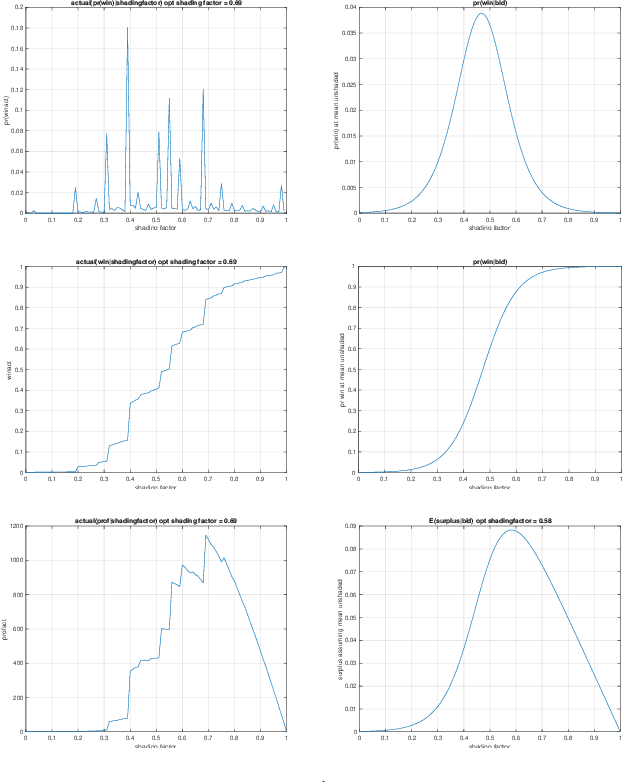

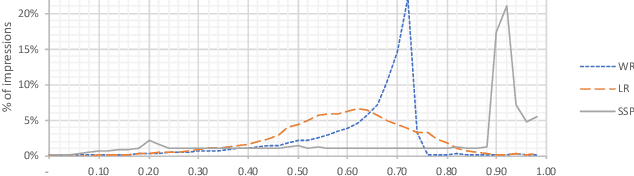

Abstract:This paper describes a new win-rate based bid shading algorithm (WR) that does not rely on the minimum-bid-to-win feedback from a Sell-Side Platform (SSP). The method uses a modified logistic regression to predict the profit from each possible shaded bid price. The function form allows fast maximization at run-time, a key requirement for Real-Time Bidding (RTB) systems. We report production results from this method along with several other algorithms. We found that bid shading, in general, can deliver significant value to advertisers, reducing price per impression to about 55% of the unshaded cost. Further, the particular approach described in this paper captures 7% more profit for advertisers, than do benchmark methods of just bidding the most probable winning price. We also report 4.3% higher surplus than an industry Sell-Side Platform shading service. Furthermore, we observed 3% - 7% lower eCPM, eCPC and eCPA when the algorithm was integrated with budget controllers. We attribute the gains above as being mainly due to the explicit maximization of the surplus function, and note that other algorithms can take advantage of this same approach.
Risk Bounds for Low Cost Bipartite Ranking
Dec 02, 2019

Abstract:Bipartite ranking is an important supervised learning problem; however, unlike regression or classification, it has a quadratic dependence on the number of samples. To circumvent the prohibitive sample cost, many recent work focus on stochastic gradient-based methods. In this paper we consider an alternative approach, which leverages the structure of the widely-adopted pairwise squared loss, to obtain a stochastic and low cost algorithm that does not require stochastic gradients or learning rates. Using a novel uniform risk bound---based on matrix and vector concentration inequalities---we show that the sample size required for competitive performance against the all-pairs batch algorithm does not have a quadratic dependence. Generalization bounds for both the batch and low cost stochastic algorithms are presented. Experimental results show significant speed gain against the batch algorithm, as well as competitive performance against state-of-the-art bipartite ranking algorithms on real datasets.
MBA: Mini-Batch AUC Optimization
May 31, 2018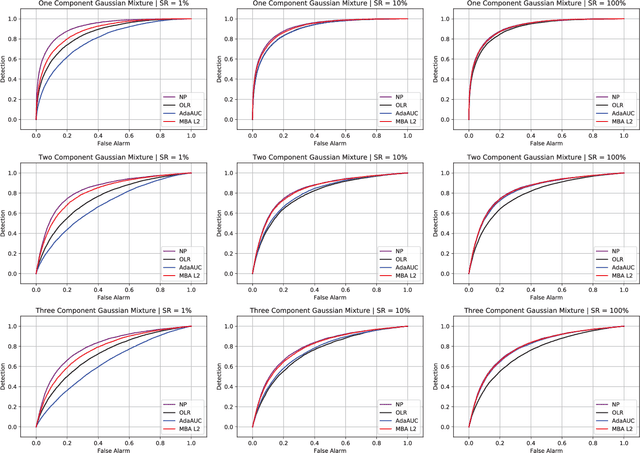
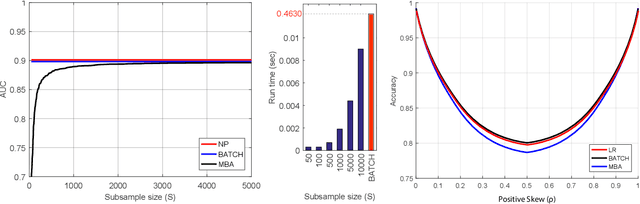
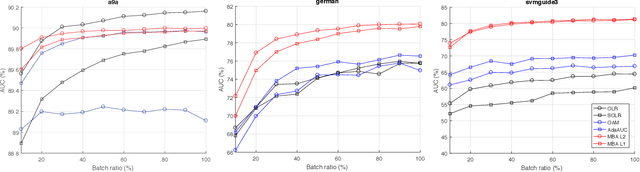
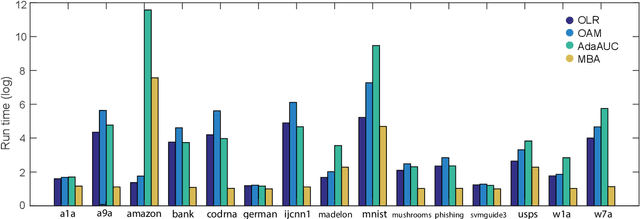
Abstract:Area under the receiver operating characteristics curve (AUC) is an important metric for a wide range of signal processing and machine learning problems, and scalable methods for optimizing AUC have recently been proposed. However, handling very large datasets remains an open challenge for this problem. This paper proposes a novel approach to AUC maximization, based on sampling mini-batches of positive/negative instance pairs and computing U-statistics to approximate a global risk minimization problem. The resulting algorithm is simple, fast, and learning-rate free. We show that the number of samples required for good performance is independent of the number of pairs available, which is a quadratic function of the positive and negative instances. Extensive experiments show the practical utility of the proposed method.
Online Forecasting Matrix Factorization
Dec 23, 2017



Abstract:In this paper the problem of forecasting high dimensional time series is considered. Such time series can be modeled as matrices where each column denotes a measurement. In addition, when missing values are present, low rank matrix factorization approaches are suitable for predicting future values. This paper formally defines and analyzes the forecasting problem in the online setting, i.e. where the data arrives as a stream and only a single pass is allowed. We present and analyze novel matrix factorization techniques which can learn low-dimensional embeddings effectively in an online manner. Based on these embeddings a recursive minimum mean square error estimator is derived, which learns an autoregressive model on them. Experiments with two real datasets with tens of millions of measurements show the benefits of the proposed approach.
Nonlinear Kalman Filtering with Divergence Minimization
May 01, 2017



Abstract:We consider the nonlinear Kalman filtering problem using Kullback-Leibler (KL) and $\alpha$-divergence measures as optimization criteria. Unlike linear Kalman filters, nonlinear Kalman filters do not have closed form Gaussian posteriors because of a lack of conjugacy due to the nonlinearity in the likelihood. In this paper we propose novel algorithms to optimize the forward and reverse forms of the KL divergence, as well as the alpha-divergence which contains these two as limiting cases. Unlike previous approaches, our algorithms do not make approximations to the divergences being optimized, but use Monte Carlo integration techniques to derive unbiased algorithms for direct optimization. We assess performance on radar and sensor tracking, and options pricing problems, showing general improvement over the UKF and EKF, as well as competitive performance with particle filtering.
Stochastic Annealing for Variational Inference
May 25, 2015



Abstract:We empirically evaluate a stochastic annealing strategy for Bayesian posterior optimization with variational inference. Variational inference is a deterministic approach to approximate posterior inference in Bayesian models in which a typically non-convex objective function is locally optimized over the parameters of the approximating distribution. We investigate an annealing method for optimizing this objective with the aim of finding a better local optimal solution and compare with deterministic annealing methods and no annealing. We show that stochastic annealing can provide clear improvement on the GMM and HMM, while performance on LDA tends to favor deterministic annealing methods.
A Collaborative Kalman Filter for Time-Evolving Dyadic Processes
Jan 22, 2015



Abstract:We present the collaborative Kalman filter (CKF), a dynamic model for collaborative filtering and related factorization models. Using the matrix factorization approach to collaborative filtering, the CKF accounts for time evolution by modeling each low-dimensional latent embedding as a multidimensional Brownian motion. Each observation is a random variable whose distribution is parameterized by the dot product of the relevant Brownian motions at that moment in time. This is naturally interpreted as a Kalman filter with multiple interacting state space vectors. We also present a method for learning a dynamically evolving drift parameter for each location by modeling it as a geometric Brownian motion. We handle posterior intractability via a mean-field variational approximation, which also preserves tractability for downstream calculations in a manner similar to the Kalman filter. We evaluate the model on several large datasets, providing quantitative evaluation on the 10 million Movielens and 100 million Netflix datasets and qualitative evaluation on a set of 39 million stock returns divided across roughly 6,500 companies from the years 1962-2014.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge