Elizabeth A. Housworth
A new class of metrics for learning on real-valued and structured data
Apr 23, 2018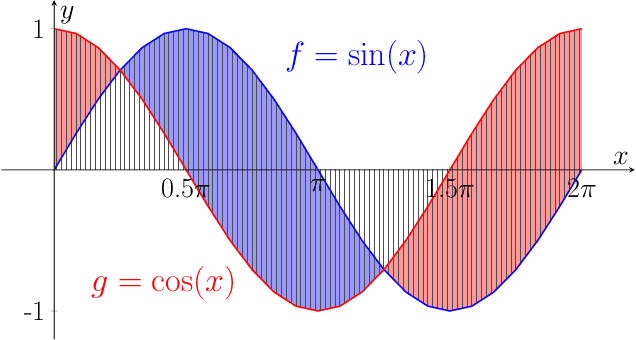
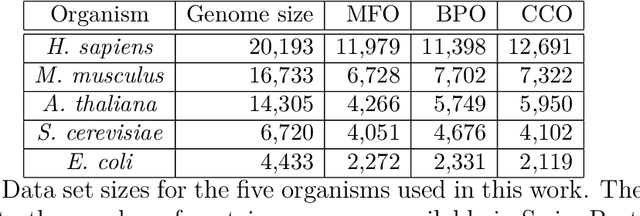
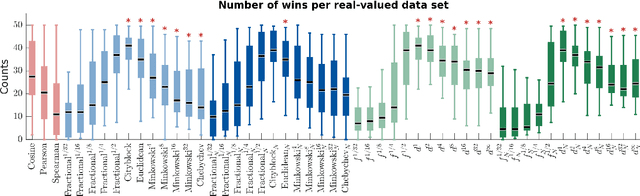
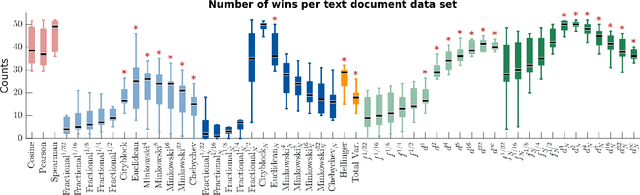
Abstract:We propose a new class of metrics on sets, vectors, and functions that can be used in various stages of data mining, including exploratory data analysis, learning, and result interpretation. These new distance functions unify and generalize some of the popular metrics, such as the Jaccard and bag distances on sets, Manhattan distance on vector spaces, and Marczewski-Steinhaus distance on integrable functions. We prove that the new metrics are complete and show useful relationships with $f$-divergences for probability distributions. To further extend our approach to structured objects such as concept hierarchies and ontologies, we introduce information-theoretic metrics on directed acyclic graphs drawn according to a fixed probability distribution. We conduct empirical investigation to demonstrate intuitive interpretation of the new metrics and their effectiveness on real-valued, high-dimensional, and structured data. Extensive comparative evaluation demonstrates that the new metrics outperformed multiple similarity and dissimilarity functions traditionally used in data mining, including the Minkowski family, the fractional $L^p$ family, two $f$-divergences, cosine distance, and two correlation coefficients. Finally, we argue that the new class of metrics is particularly appropriate for rapid processing of high-dimensional and structured data in distance-based learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge