TouchAnything: A Dataset and Framework for Bimanual Tactile Estimation from Egocentric Video

Egocentric human video data, which captures rich human-environment interactions and can be collected at scale, has become a key driver of embodied intelligence research. However, existing egocentric datasets typically lack tactile sensing, a critical modality that provides direct cues about contact, force, and pressure in human-object interaction. Without such signals, models struggle to learn physically grounded representations of real-world interaction dynamics. While tactile sensors provide these cues, deploying high-quality tactile hardware at scale remains expensive and cumbersome. This raises a central question: can tactile feedback be inferred directly from visual observations, enabling scalable tactile supervision for egocentric video data and supporting physically grounded embodied learning? To enable research in this direction, we introduce EgoTouch, a large-scale multi-view egocentric dataset with dense tactile supervision for bimanual hand-object interaction. EgoTouch comprises 208 manipulation tasks spanning 1,891 episodes in diverse indoor and outdoor environments, with synchronized multi-view RGB (head-mounted egocentric and dual wrist-mounted cameras), bimanual 3D hand pose, and continuous pressure maps from wearable tactile sensors. Building on EgoTouch, we introduce TouchAnything, a baseline multi-view vision-to-touch prediction framework that uses the egocentric view as the primary input and flexibly leverages available wrist-mounted views at inference time. Experiments show that incorporating wrist-mounted views generally improves tactile prediction over egocentric-only input, achieving up to 5.0% relative improvement in Contact IoU and 6.1% relative improvement in Volumetric IoU. We will publicly release the dataset, code, and benchmark.

Dive into Big Model Training

The increasing scale of model size and continuous improvement of performance herald the arrival of the Big Model era. In this report, we explore what and how the big model training works by diving into training objectives and training methodologies. Specifically,training objectives describe how to leverage web-scale data to develop extremely capable and incredibly large models based on self-supervised learning, and training methodologies which are based on distributed training describe how to make big model training a reality. We summarize the existing training methodologies into three main categories: training parallelism, memory-saving technologies, and model sparsity design. Training parallelism can be categorized into data, pipeline, and tensor parallelism according to the dimension of parallelism that takes place. Memory-saving technologies are orthogonal and complementary to training parallelism. And model sparsity design further scales up the model size with a constant computational cost. A continuously updated paper list of big model training is provided at https://github.com/qhliu26/BM-Training.

A new class of metrics for learning on real-valued and structured data

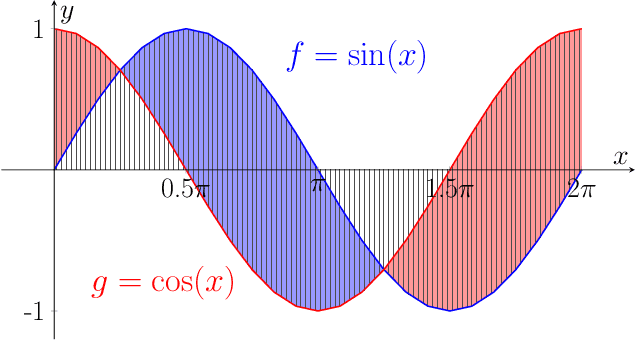
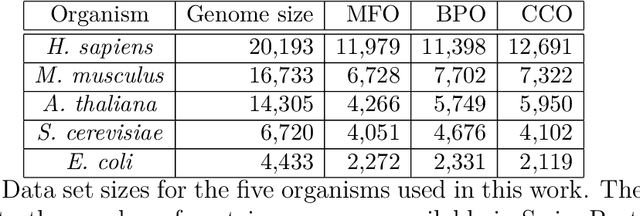
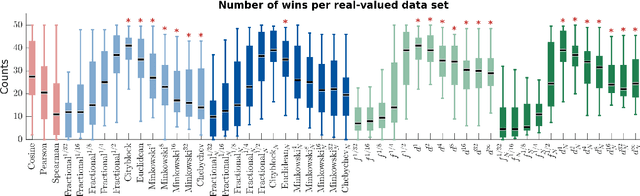
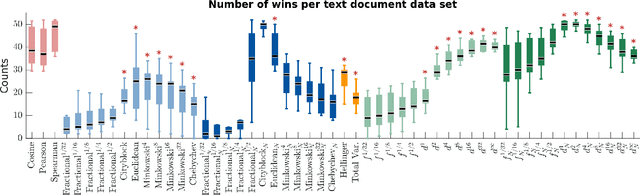
We propose a new class of metrics on sets, vectors, and functions that can be used in various stages of data mining, including exploratory data analysis, learning, and result interpretation. These new distance functions unify and generalize some of the popular metrics, such as the Jaccard and bag distances on sets, Manhattan distance on vector spaces, and Marczewski-Steinhaus distance on integrable functions. We prove that the new metrics are complete and show useful relationships with $f$-divergences for probability distributions. To further extend our approach to structured objects such as concept hierarchies and ontologies, we introduce information-theoretic metrics on directed acyclic graphs drawn according to a fixed probability distribution. We conduct empirical investigation to demonstrate intuitive interpretation of the new metrics and their effectiveness on real-valued, high-dimensional, and structured data. Extensive comparative evaluation demonstrates that the new metrics outperformed multiple similarity and dissimilarity functions traditionally used in data mining, including the Minkowski family, the fractional $L^p$ family, two $f$-divergences, cosine distance, and two correlation coefficients. Finally, we argue that the new class of metrics is particularly appropriate for rapid processing of high-dimensional and structured data in distance-based learning.