Efficient Estimation of Kernel Surrogate Models for Task Attribution

Modern AI agents such as large language models are trained on diverse tasks -- translation, code generation, mathematical reasoning, and text prediction -- simultaneously. A key question is to quantify how each individual training task influences performance on a target task, a problem we refer to as task attribution. The direct approach, leave-one-out retraining, measures the effect of removing each task, but is computationally infeasible at scale. An alternative approach that builds surrogate models to predict a target task's performance for any subset of training tasks has emerged in recent literature. Prior work focuses on linear surrogate models, which capture first-order relationships, but miss nonlinear interactions such as synergy, antagonism, or XOR-type effects. In this paper, we first consider a unified task weighting framework for analyzing task attribution methods, and show a new connection between linear surrogate models and influence functions through a second-order analysis. Then, we introduce kernel surrogate models, which more effectively represent second-order task interactions. To efficiently learn the kernel surrogate, we develop a gradient-based estimation procedure that leverages a first-order approximation of pretrained models; empirically, this yields accurate estimates with less than $2\%$ relative error without repeated retraining. Experiments across multiple domains -- including math reasoning in transformers, in-context learning, and multi-objective reinforcement learning -- demonstrate the effectiveness of kernel surrogate models. They achieve a $25\%$ higher correlation with the leave-one-out ground truth than linear surrogates and influence-function baselines. When used for downstream task selection, kernel surrogate models yield a $40\%$ improvement in demonstration selection for in-context learning and multi-objective reinforcement learning benchmarks.

One-Sided Matrix Completion from Ultra-Sparse Samples

Matrix completion is a classical problem that has received recurring interest across a wide range of fields. In this paper, we revisit this problem in an ultra-sparse sampling regime, where each entry of an unknown, $n\times d$ matrix $M$ (with $n \ge d$) is observed independently with probability $p = C / d$, for a fixed integer $C \ge 2$. This setting is motivated by applications involving large, sparse panel datasets, where the number of rows far exceeds the number of columns. When each row contains only $C$ entries -- fewer than the rank of $M$ -- accurate imputation of $M$ is impossible. Instead, we estimate the row span of $M$ or the averaged second-moment matrix $T = M^{\top} M / n$. The empirical second-moment matrix computed from observed entries exhibits non-random and sparse missingness. We propose an unbiased estimator that normalizes each nonzero entry of the second moment by its observed frequency, followed by gradient descent to impute the missing entries of $T$. The normalization divides a weighted sum of $n$ binomial random variables by the total number of ones. We show that the estimator is unbiased for any $p$ and enjoys low variance. When the row vectors of $M$ are drawn uniformly from a rank-$r$ factor model satisfying an incoherence condition, we prove that if $n \ge O({d r^5 ε^{-2} C^{-2} \log d})$, any local minimum of the gradient-descent objective is approximately global and recovers $T$ with error at most $ε^2$. Experiments on both synthetic and real-world data validate our approach. On three MovieLens datasets, our algorithm reduces bias by $88\%$ relative to baseline estimators. We also empirically validate the linear sampling complexity of $n$ relative to $d$ on synthetic data. On an Amazon reviews dataset with sparsity $10^{-7}$, our method reduces the recovery error of $T$ by $59\%$ and $M$ by $38\%$ compared to baseline methods.

Scalable Multi-Objective and Meta Reinforcement Learning via Gradient Estimation

We study the problem of efficiently estimating policies that simultaneously optimize multiple objectives in reinforcement learning (RL). Given $n$ objectives (or tasks), we seek the optimal partition of these objectives into $k \ll n$ groups, where each group comprises related objectives that can be trained together. This problem arises in applications such as robotics, control, and preference optimization in language models, where learning a single policy for all $n$ objectives is suboptimal as $n$ grows. We introduce a two-stage procedure -- meta-training followed by fine-tuning -- to address this problem. We first learn a meta-policy for all objectives using multitask learning. Then, we adapt the meta-policy to multiple randomly sampled subsets of objectives. The adaptation step leverages a first-order approximation property of well-trained policy networks, which is empirically verified to be accurate within a $2\%$ error margin across various RL environments. The resulting algorithm, PolicyGradEx, efficiently estimates an aggregate task-affinity score matrix given a policy evaluation algorithm. Based on the estimated affinity score matrix, we cluster the $n$ objectives into $k$ groups by maximizing the intra-cluster affinity scores. Experiments on three robotic control and the Meta-World benchmarks demonstrate that our approach outperforms state-of-the-art baselines by $16\%$ on average, while delivering up to $26\times$ faster speedup relative to performing full training to obtain the clusters. Ablation studies validate each component of our approach. For instance, compared with random grouping and gradient-similarity-based grouping, our loss-based clustering yields an improvement of $19\%$. Finally, we analyze the generalization error of policy networks by measuring the Hessian trace of the loss surface, which gives non-vacuous measures relative to the observed generalization errors.

Linear-Time Demonstration Selection for In-Context Learning via Gradient Estimation

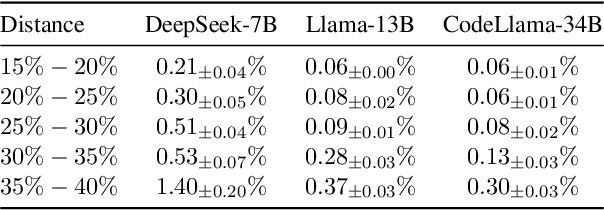
This paper introduces an algorithm to select demonstration examples for in-context learning of a query set. Given a set of $n$ examples, how can we quickly select $k$ out of $n$ to best serve as the conditioning for downstream inference? This problem has broad applications in prompt tuning and chain-of-thought reasoning. Since model weights remain fixed during in-context learning, previous work has sought to design methods based on the similarity of token embeddings. This work proposes a new approach based on gradients of the output taken in the input embedding space. Our approach estimates model outputs through a first-order approximation using the gradients. Then, we apply this estimation to multiple randomly sampled subsets. Finally, we aggregate the sampled subset outcomes to form an influence score for each demonstration, and select $k$ most relevant examples. This procedure only requires pre-computing model outputs and gradients once, resulting in a linear-time algorithm relative to model and training set sizes. Extensive experiments across various models and datasets validate the efficiency of our approach. We show that the gradient estimation procedure yields approximations of full inference with less than $\mathbf{1}\%$ error across six datasets. This allows us to scale up subset selection that would otherwise run full inference by up to $\mathbf{37.7}\times$ on models with up to $34$ billion parameters, and outperform existing selection methods based on input embeddings by $\mathbf{11}\%$ on average.

Efficient Ensemble for Fine-tuning Language Models on Multiple Datasets

This paper develops an ensemble method for fine-tuning a language model to multiple datasets. Existing methods, such as quantized LoRA (QLoRA), are efficient when adapting to a single dataset. When training on multiple datasets of different tasks, a common setup in practice, it remains unclear how to design an efficient adaptation for fine-tuning language models. We propose to use an ensemble of multiple smaller adapters instead of a single adapter per task. We design an efficient algorithm that partitions $n$ datasets into $m$ groups, where $m$ is typically much smaller than $n$ in practice, and train one adapter for each group before taking a weighted combination to form the ensemble. The algorithm leverages a first-order approximation property of low-rank adaptation to quickly obtain the fine-tuning performances of dataset combinations since methods like LoRA stay close to the base model. Hence, we use the gradients of the base model to estimate its behavior during fine-tuning. Empirically, this approximation holds with less than $1\%$ error on models with up to $34$ billion parameters, leading to an estimation of true fine-tuning performances under $5\%$ error while speeding up computation compared to base fine-tuning by $105$ times. When applied to fine-tune Llama and GPT models on ten text classification tasks, our approach provides up to $10\%$ higher average test accuracy over QLoRA, with only $9\%$ more FLOPs. On a Llama model with $34$ billion parameters, an ensemble of QLoRA increases test accuracy by $3\%$ compared to QLoRA, with only $8\%$ more FLOPs.

Scalable Fine-tuning from Multiple Data Sources:A First-Order Approximation Approach

We study the problem of fine-tuning a language model (LM) for a target task by optimally using the information from $n$ auxiliary tasks. This problem has broad applications in NLP, such as targeted instruction tuning and data selection in chain-of-thought fine-tuning. The key challenge of this problem is that not all auxiliary tasks are useful to improve the performance of the target task. Thus, choosing the right subset of auxiliary tasks is crucial. Conventional subset selection methods, such as forward & backward selection, are unsuitable for LM fine-tuning because they require repeated training on subsets of auxiliary tasks. This paper introduces a new algorithm to estimate model fine-tuning performances without repeated training. Our algorithm first performs multitask training using the data of all the tasks to obtain a meta initialization. Then, we approximate the model fine-tuning loss of a subset using functional values and gradients from the meta initialization. Empirically, we find that this gradient-based approximation holds with remarkable accuracy for twelve transformer-based LMs. Thus, we can now estimate fine-tuning performances on CPUs within a few seconds. We conduct extensive experiments to validate our approach, delivering a speedup of $30\times$ over conventional subset selection while incurring only $1\%$ error of the true fine-tuning performances. In downstream evaluations of instruction tuning and chain-of-thought fine-tuning, our approach improves over prior methods that utilize gradient or representation similarity for subset selection by up to $3.8\%$.

Scalable Multitask Learning Using Gradient-based Estimation of Task Affinity

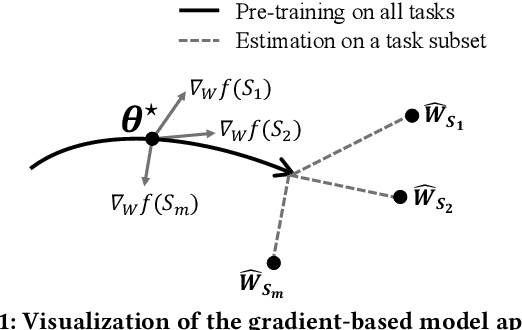
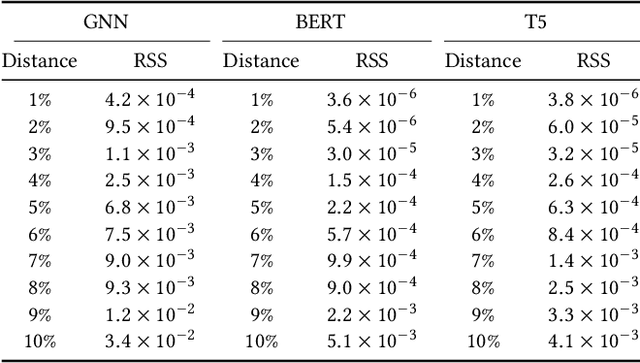
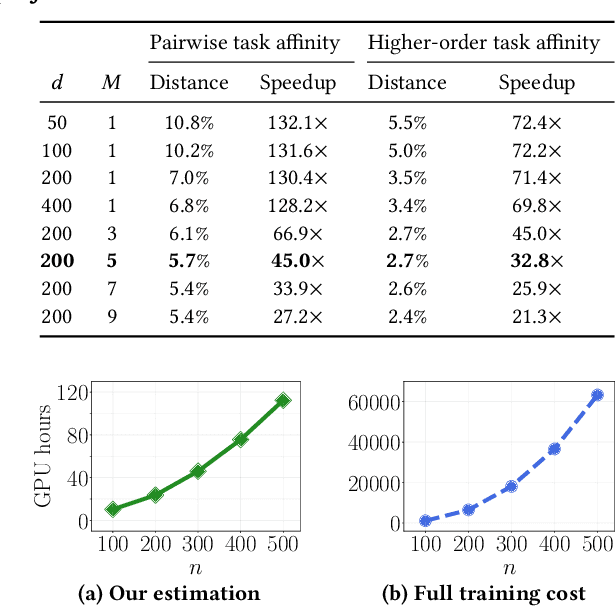
Multitask learning is a widely used paradigm for training models on diverse tasks, with applications ranging from graph neural networks to language model fine-tuning. Since tasks may interfere with each other, a key notion for modeling their relationships is task affinity. This includes pairwise task affinity, computed among pairs of tasks, and higher-order affinity, computed among subsets of tasks. Naively computing either of them requires repeatedly training on data from various task combinations, which is computationally intensive. We present a new algorithm Grad-TAG that can estimate task affinities without this repeated training. The key idea of Grad-TAG is to train a "base" model for all tasks and then use a linearization technique to estimate the loss of the model for a specific task combination. The linearization works by computing a gradient-based approximation of the loss, using low-dimensional projections of gradients as features in a logistic regression to predict labels for the task combination. We show that the linearized model can provably approximate the loss when the gradient-based approximation is accurate, and also empirically verify that on several large models. Then, given the estimated task affinity, we design a semi-definite program for clustering similar tasks by maximizing the average density of clusters. We evaluate Grad-TAG's performance across seven datasets, including multi-label classification on graphs, and instruction fine-tuning of language models. Our task affinity estimates are within 2.7% distance to the true affinities while needing only 3% of FLOPs in full training. On our largest graph with 21M edges and 500 labeling tasks, our algorithm delivers estimates within 5% distance to the true affinities, using only 112 GPU hours. Our results show that Grad-TAG achieves excellent performance and runtime tradeoffs compared to existing approaches.

Learning Tree-Structured Composition of Data Augmentation

Data augmentation is widely used for training a neural network given little labeled data. A common practice of augmentation training is applying a composition of multiple transformations sequentially to the data. Existing augmentation methods such as RandAugment randomly sample from a list of pre-selected transformations, while methods such as AutoAugment apply advanced search to optimize over an augmentation set of size $k^d$, which is the number of transformation sequences of length $d$, given a list of $k$ transformations. In this paper, we design efficient algorithms whose running time complexity is much faster than the worst-case complexity of $O(k^d)$, provably. We propose a new algorithm to search for a binary tree-structured composition of $k$ transformations, where each tree node corresponds to one transformation. The binary tree generalizes sequential augmentations, such as the SimCLR augmentation scheme for contrastive learning. Using a top-down, recursive search procedure, our algorithm achieves a runtime complexity of $O(2^d k)$, which is much faster than $O(k^d)$ as $k$ increases above $2$. We apply our algorithm to tackle data distributions with heterogeneous subpopulations by searching for one tree in each subpopulation and then learning a weighted combination, resulting in a forest of trees. We validate our proposed algorithms on numerous graph and image datasets, including a multi-label graph classification dataset we collected. The dataset exhibits significant variations in the sizes of graphs and their average degrees, making it ideal for studying data augmentation. We show that our approach can reduce the computation cost by 43% over existing search methods while improving performance by 4.3%. The tree structures can be used to interpret the relative importance of each transformation, such as identifying the important transformations on small vs. large graphs.

Graph Neural Networks for Road Safety Modeling: Datasets and Evaluations for Accident Analysis

We consider the problem of traffic accident analysis on a road network based on road network connections and traffic volume. Previous works have designed various deep-learning methods using historical records to predict traffic accident occurrences. However, there is a lack of consensus on how accurate existing methods are, and a fundamental issue is the lack of public accident datasets for comprehensive evaluations. This paper constructs a large-scale, unified dataset of traffic accident records from official reports of various states in the US, totaling 9 million records, accompanied by road networks and traffic volume reports. Using this new dataset, we evaluate existing deep-learning methods for predicting the occurrence of accidents on road networks. Our main finding is that graph neural networks such as GraphSAGE can accurately predict the number of accidents on roads with less than 22% mean absolute error (relative to the actual count) and whether an accident will occur or not with over 87% AUROC, averaged over states. We achieve these results by using multitask learning to account for cross-state variabilities (e.g., availability of accident labels) and transfer learning to combine traffic volume with accident prediction. Ablation studies highlight the importance of road graph-structural features, amongst other features. Lastly, we discuss the implications of the analysis and develop a package for easily using our new dataset.

Boosting Multitask Learning on Graphs through Higher-Order Task Affinities

Predicting node labels on a given graph is a widely studied problem with many applications, including community detection and molecular graph prediction. This paper considers predicting multiple node labeling functions on graphs simultaneously and revisits this problem from a multitask learning perspective. For a concrete example, consider overlapping community detection: each community membership is a binary node classification task. Due to complex overlapping patterns, we find that negative transfer is prevalent when we apply naive multitask learning to multiple community detection, as task relationships are highly nonlinear across different node labeling. To address the challenge, we develop an algorithm to cluster tasks into groups based on a higher-order task affinity measure. We then fit a multitask model on each task group, resulting in a boosting procedure on top of the baseline model. We estimate the higher-order task affinity measure between two tasks as the prediction loss of one task in the presence of another task and a random subset of other tasks. Then, we use spectral clustering on the affinity score matrix to identify task grouping. We design several speedup techniques to compute the higher-order affinity scores efficiently and show that they can predict negative transfers more accurately than pairwise task affinities. We validate our procedure using various community detection and molecular graph prediction data sets, showing favorable results compared with existing methods. Lastly, we provide a theoretical analysis to show that under a planted block model of tasks on graphs, our affinity scores can provably separate tasks into groups.