Aneesh Sharma
Scalable Multitask Learning Using Gradient-based Estimation of Task Affinity
Sep 09, 2024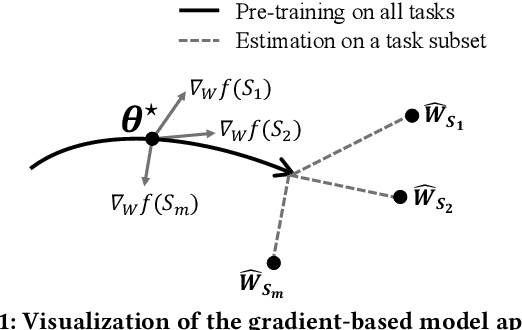
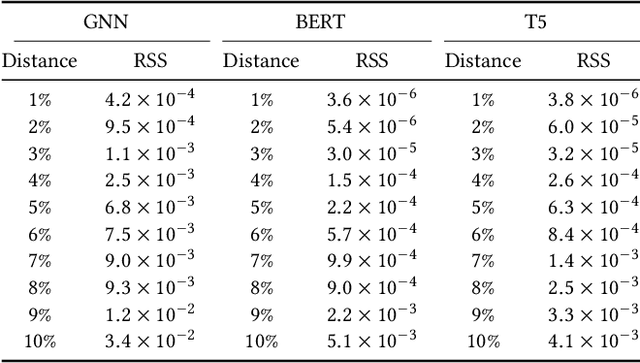

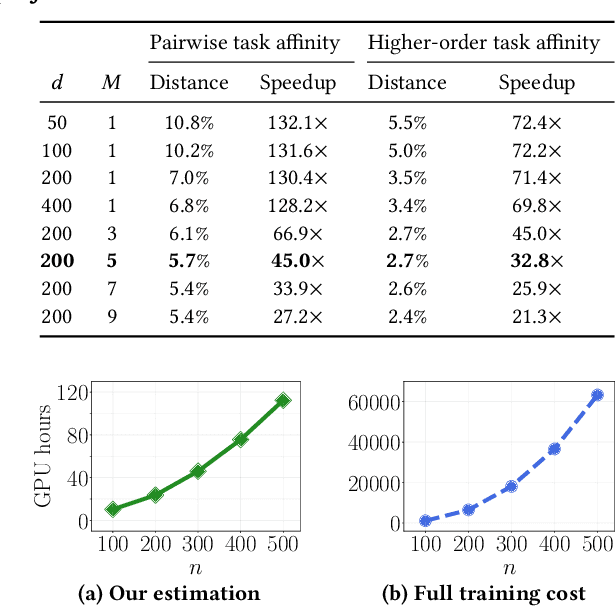
Abstract:Multitask learning is a widely used paradigm for training models on diverse tasks, with applications ranging from graph neural networks to language model fine-tuning. Since tasks may interfere with each other, a key notion for modeling their relationships is task affinity. This includes pairwise task affinity, computed among pairs of tasks, and higher-order affinity, computed among subsets of tasks. Naively computing either of them requires repeatedly training on data from various task combinations, which is computationally intensive. We present a new algorithm Grad-TAG that can estimate task affinities without this repeated training. The key idea of Grad-TAG is to train a "base" model for all tasks and then use a linearization technique to estimate the loss of the model for a specific task combination. The linearization works by computing a gradient-based approximation of the loss, using low-dimensional projections of gradients as features in a logistic regression to predict labels for the task combination. We show that the linearized model can provably approximate the loss when the gradient-based approximation is accurate, and also empirically verify that on several large models. Then, given the estimated task affinity, we design a semi-definite program for clustering similar tasks by maximizing the average density of clusters. We evaluate Grad-TAG's performance across seven datasets, including multi-label classification on graphs, and instruction fine-tuning of language models. Our task affinity estimates are within 2.7% distance to the true affinities while needing only 3% of FLOPs in full training. On our largest graph with 21M edges and 500 labeling tasks, our algorithm delivers estimates within 5% distance to the true affinities, using only 112 GPU hours. Our results show that Grad-TAG achieves excellent performance and runtime tradeoffs compared to existing approaches.
Boosting Multitask Learning on Graphs through Higher-Order Task Affinities
Jun 24, 2023



Abstract:Predicting node labels on a given graph is a widely studied problem with many applications, including community detection and molecular graph prediction. This paper considers predicting multiple node labeling functions on graphs simultaneously and revisits this problem from a multitask learning perspective. For a concrete example, consider overlapping community detection: each community membership is a binary node classification task. Due to complex overlapping patterns, we find that negative transfer is prevalent when we apply naive multitask learning to multiple community detection, as task relationships are highly nonlinear across different node labeling. To address the challenge, we develop an algorithm to cluster tasks into groups based on a higher-order task affinity measure. We then fit a multitask model on each task group, resulting in a boosting procedure on top of the baseline model. We estimate the higher-order task affinity measure between two tasks as the prediction loss of one task in the presence of another task and a random subset of other tasks. Then, we use spectral clustering on the affinity score matrix to identify task grouping. We design several speedup techniques to compute the higher-order affinity scores efficiently and show that they can predict negative transfers more accurately than pairwise task affinities. We validate our procedure using various community detection and molecular graph prediction data sets, showing favorable results compared with existing methods. Lastly, we provide a theoretical analysis to show that under a planted block model of tasks on graphs, our affinity scores can provably separate tasks into groups.
Generalization in Graph Neural Networks: Improved PAC-Bayesian Bounds on Graph Diffusion
Feb 09, 2023Abstract:Graph neural networks are widely used tools for graph prediction tasks. Motivated by their empirical performance, prior works have developed generalization bounds for graph neural networks, which scale with graph structures in terms of the maximum degree. In this paper, we present generalization bounds that instead scale with the largest singular value of the graph neural network's feature diffusion matrix. These bounds are numerically much smaller than prior bounds for real-world graphs. We also construct a lower bound of the generalization gap that matches our upper bound asymptotically. To achieve these results, we analyze a unified model that includes prior works' settings (i.e., convolutional and message-passing networks) and new settings (i.e., graph isomorphism networks). Our key idea is to measure the stability of graph neural networks against noise perturbations using Hessians. Empirically, we find that Hessian-based measurements correlate with the observed generalization gaps of graph neural networks accurately; Optimizing noise stability properties for fine-tuning pretrained graph neural networks also improves test performance on several graph-level classification tasks.
Classic Graph Structural Features Outperform Factorization-Based Graph Embedding Methods on Community Labeling
Jan 20, 2022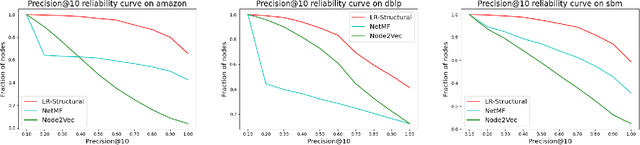
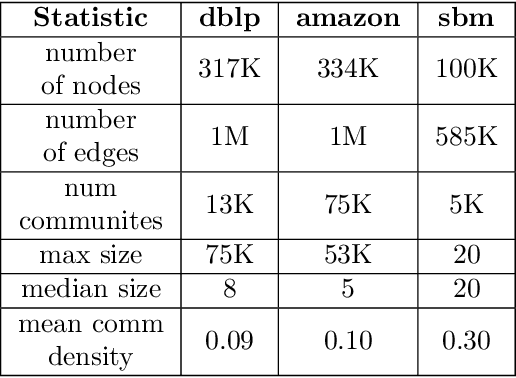
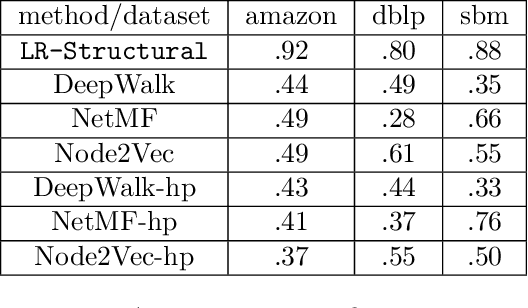

Abstract:Graph representation learning (also called graph embeddings) is a popular technique for incorporating network structure into machine learning models. Unsupervised graph embedding methods aim to capture graph structure by learning a low-dimensional vector representation (the embedding) for each node. Despite the widespread use of these embeddings for a variety of downstream transductive machine learning tasks, there is little principled analysis of the effectiveness of this approach for common tasks. In this work, we provide an empirical and theoretical analysis for the performance of a class of embeddings on the common task of pairwise community labeling. This is a binary variant of the classic community detection problem, which seeks to build a classifier to determine whether a pair of vertices participate in a community. In line with our goal of foundational understanding, we focus on a popular class of unsupervised embedding techniques that learn low rank factorizations of a vertex proximity matrix (this class includes methods like GraRep, DeepWalk, node2vec, NetMF). We perform detailed empirical analysis for community labeling over a variety of real and synthetic graphs with ground truth. In all cases we studied, the models trained from embedding features perform poorly on community labeling. In constrast, a simple logistic model with classic graph structural features handily outperforms the embedding models. For a more principled understanding, we provide a theoretical analysis for the (in)effectiveness of these embeddings in capturing the community structure. We formally prove that popular low-dimensional factorization methods either cannot produce community structure, or can only produce ``unstable" communities. These communities are inherently unstable under small perturbations.
The impossibility of low rank representations for triangle-rich complex networks
Mar 27, 2020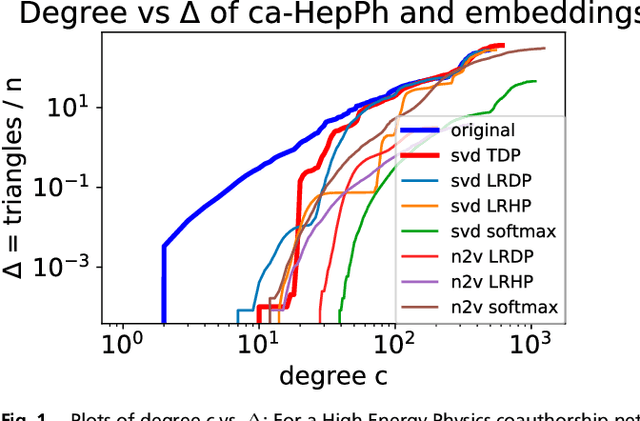
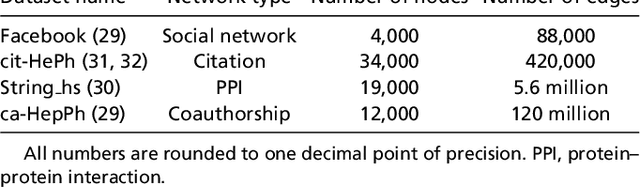
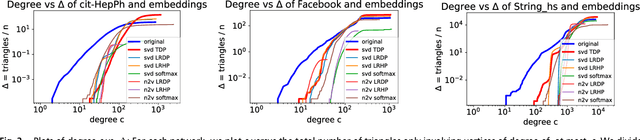
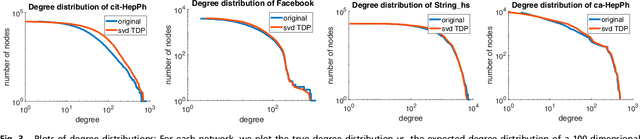
Abstract:The study of complex networks is a significant development in modern science, and has enriched the social sciences, biology, physics, and computer science. Models and algorithms for such networks are pervasive in our society, and impact human behavior via social networks, search engines, and recommender systems to name a few. A widely used algorithmic technique for modeling such complex networks is to construct a low-dimensional Euclidean embedding of the vertices of the network, where proximity of vertices is interpreted as the likelihood of an edge. Contrary to the common view, we argue that such graph embeddings do not}capture salient properties of complex networks. The two properties we focus on are low degree and large clustering coefficients, which have been widely established to be empirically true for real-world networks. We mathematically prove that any embedding (that uses dot products to measure similarity) that can successfully create these two properties must have rank nearly linear in the number of vertices. Among other implications, this establishes that popular embedding techniques such as Singular Value Decomposition and node2vec fail to capture significant structural aspects of real-world complex networks. Furthermore, we empirically study a number of different embedding techniques based on dot product, and show that they all fail to capture the triangle structure.
LSF-Join: Locality Sensitive Filtering for Distributed All-Pairs Set Similarity Under Skew
Mar 06, 2020



Abstract:All-pairs set similarity is a widely used data mining task, even for large and high-dimensional datasets. Traditionally, similarity search has focused on discovering very similar pairs, for which a variety of efficient algorithms are known. However, recent work highlights the importance of finding pairs of sets with relatively small intersection sizes. For example, in a recommender system, two users may be alike even though their interests only overlap on a small percentage of items. In such systems, some dimensions are often highly skewed because they are very popular. Together these two properties render previous approaches infeasible for large input sizes. To address this problem, we present a new distributed algorithm, LSF-Join, for approximate all-pairs set similarity. The core of our algorithm is a randomized selection procedure based on Locality Sensitive Filtering. Our method deviates from prior approximate algorithms, which are based on Locality Sensitive Hashing. Theoretically, we show that LSF-Join efficiently finds most close pairs, even for small similarity thresholds and for skewed input sets. We prove guarantees on the communication, work, and maximum load of LSF-Join, and we also experimentally demonstrate its accuracy on multiple graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge