Locally optimal detection of stochastic targeted universal adversarial perturbations

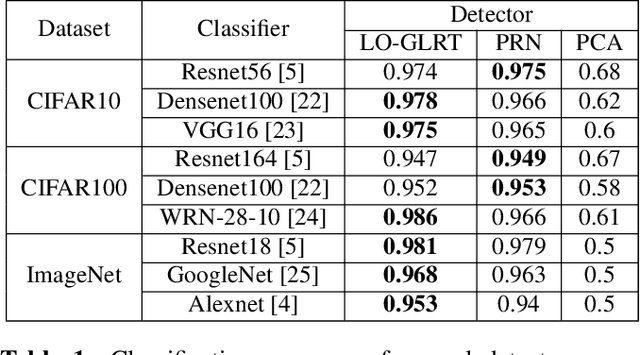
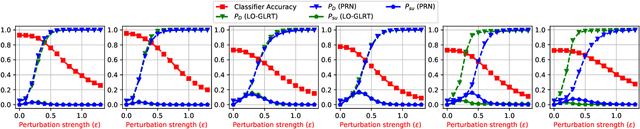
Deep learning image classifiers are known to be vulnerable to small adversarial perturbations of input images. In this paper, we derive the locally optimal generalized likelihood ratio test (LO-GLRT) based detector for detecting stochastic targeted universal adversarial perturbations (UAPs) of the classifier inputs. We also describe a supervised training method to learn the detector's parameters, and demonstrate better performance of the detector compared to other detection methods on several popular image classification datasets.

Robust Machine Learning via Privacy/Rate-Distortion Theory

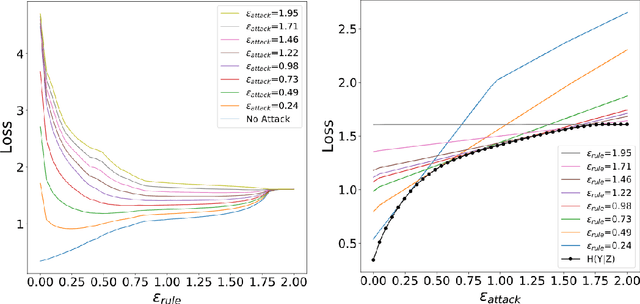
Robust machine learning formulations have emerged to address the prevalent vulnerability of deep neural networks to adversarial examples. Our work draws the connection between optimal robust learning and the privacy-utility tradeoff problem, which is a generalization of the rate-distortion problem. The saddle point of the game between a robust classifier and an adversarial perturbation can be found via the solution of a maximum conditional entropy problem. This information-theoretic perspective sheds light on the fundamental tradeoff between robustness and clean data performance, which ultimately arises from the geometric structure of the underlying data distribution and perturbation constraints. Further, we show that under mild conditions, the worst case adversarial distribution with Wasserstein-ball constraints on the perturbation has a fixed point characterization. This is obtained via the first order necessary conditions for optimality of the derived maximum conditional entropy problem. This fixed point characterization exposes the interplay between the geometry of the ground cost in the Wasserstein-ball constraint, the worst-case adversarial distribution, and the given reference data distribution.

Detecting Audio Attacks on ASR Systems with Dropout Uncertainty

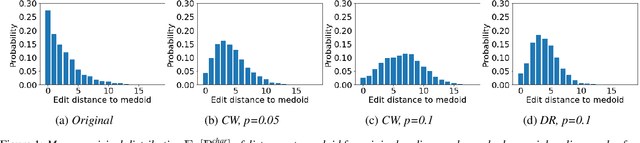
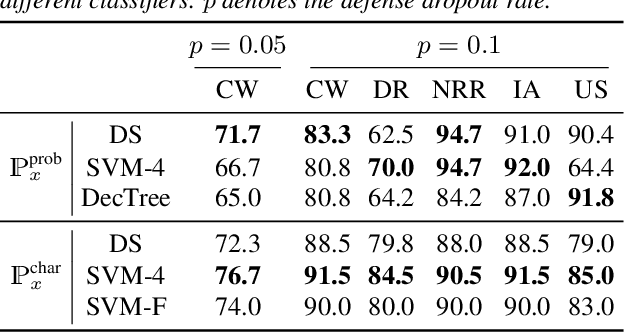
Various adversarial audio attacks have recently been developed to fool automatic speech recognition (ASR) systems. We here propose a defense against such attacks based on the uncertainty introduced by dropout in neural networks. We show that our defense is able to detect attacks created through optimized perturbations and frequency masking on a state-of-the-art end-to-end ASR system. Furthermore, the defense can be made robust against attacks that are immune to noise reduction. We test our defense on Mozilla's CommonVoice dataset, the UrbanSound dataset, and an excerpt of the LibriSpeech dataset, showing that it achieves high detection accuracy in a wide range of scenarios.

Faster Subgradient Methods for Functions with Hölderian Growth

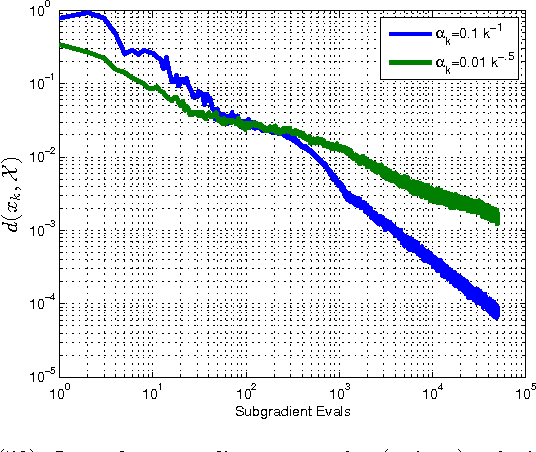
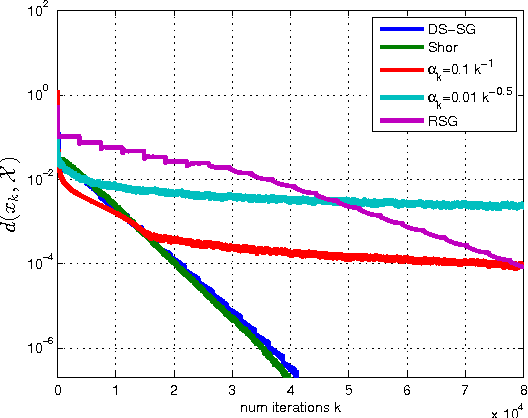
The purpose of this manuscript is to derive new convergence results for several subgradient methods applied to minimizing nonsmooth convex functions with H\"olderian growth. The growth condition is satisfied in many applications and includes functions with quadratic growth and weakly sharp minima as special cases. To this end there are three main contributions. First, for a constant and sufficiently small stepsize, we show that the subgradient method achieves linear convergence up to a certain region including the optimal set, with error of the order of the stepsize. Second, if appropriate problem parameters are known, we derive a decaying stepsize which obtains a much faster convergence rate than is suggested by the classical $O(1/\sqrt{k})$ result for the subgradient method. Thirdly we develop a novel "descending stairs" stepsize which obtains this faster convergence rate and also obtains linear convergence for the special case of weakly sharp functions. We also develop an adaptive variant of the "descending stairs" stepsize which achieves the same convergence rate without requiring an error bound constant which is difficult to estimate in practice.

Variable-Length Hashing

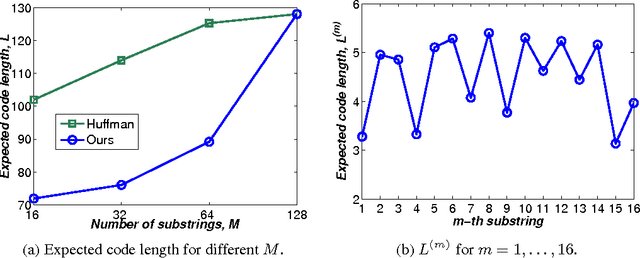
Hashing has emerged as a popular technique for large-scale similarity search. Most learning-based hashing methods generate compact yet correlated hash codes. However, this redundancy is storage-inefficient. Hence we propose a lossless variable-length hashing (VLH) method that is both storage- and search-efficient. Storage efficiency is achieved by converting the fixed-length hash code into a variable-length code. Search efficiency is obtained by using a multiple hash table structure. With VLH, we are able to deliberately add redundancy into hash codes to improve retrieval performance with little sacrifice in storage efficiency or search complexity. In particular, we propose a block K-means hashing (B-KMH) method to obtain significantly improved retrieval performance with no increase in storage and marginal increase in computational cost.

Local and Global Convergence of a General Inertial Proximal Splitting Scheme

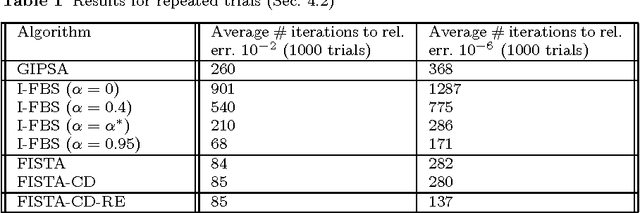
This paper is concerned with convex composite minimization problems in a Hilbert space. In these problems, the objective is the sum of two closed, proper, and convex functions where one is smooth and the other admits a computationally inexpensive proximal operator. We analyze a general family of inertial proximal splitting algorithms (GIPSA) for solving such problems. We establish finiteness of the sum of squared increments of the iterates and optimality of the accumulation points. Weak convergence of the entire sequence then follows if the minimum is attained. Our analysis unifies and extends several previous results. We then focus on $\ell_1$-regularized optimization, which is the ubiquitous special case where the nonsmooth term is the $\ell_1$-norm. For certain parameter choices, GIPSA is amenable to a local analysis for this problem. For these choices we show that GIPSA achieves finite "active manifold identification", i.e. convergence in a finite number of iterations to the optimal support and sign, after which GIPSA reduces to minimizing a local smooth function. Local linear convergence then holds under certain conditions. We determine the rate in terms of the inertia, stepsize, and local curvature. Our local analysis is applicable to certain recent variants of the Fast Iterative Shrinkage-Thresholding Algorithm (FISTA), for which we establish active manifold identification and local linear convergence. Our analysis motivates the use of a momentum restart scheme in these FISTA variants to obtain the optimal local linear convergence rate.

Learning from Collective Intelligence in Groups

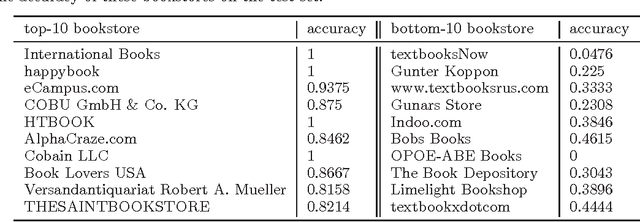
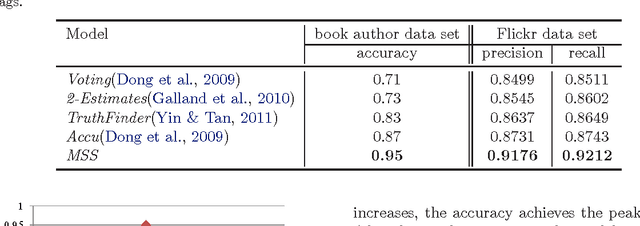
Collective intelligence, which aggregates the shared information from large crowds, is often negatively impacted by unreliable information sources with the low quality data. This becomes a barrier to the effective use of collective intelligence in a variety of applications. In order to address this issue, we propose a probabilistic model to jointly assess the reliability of sources and find the true data. We observe that different sources are often not independent of each other. Instead, sources are prone to be mutually influenced, which makes them dependent when sharing information with each other. High dependency between sources makes collective intelligence vulnerable to the overuse of redundant (and possibly incorrect) information from the dependent sources. Thus, we reveal the latent group structure among dependent sources, and aggregate the information at the group level rather than from individual sources directly. This can prevent the collective intelligence from being inappropriately dominated by dependent sources. We will also explicitly reveal the reliability of groups, and minimize the negative impacts of unreliable groups. Experimental results on real-world data sets show the effectiveness of the proposed approach with respect to existing algorithms.