Local and Global Convergence of a General Inertial Proximal Splitting Scheme
Paper and Code
Feb 08, 2016
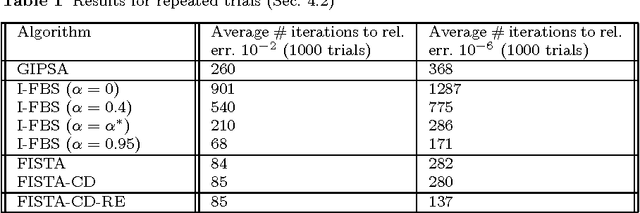
This paper is concerned with convex composite minimization problems in a Hilbert space. In these problems, the objective is the sum of two closed, proper, and convex functions where one is smooth and the other admits a computationally inexpensive proximal operator. We analyze a general family of inertial proximal splitting algorithms (GIPSA) for solving such problems. We establish finiteness of the sum of squared increments of the iterates and optimality of the accumulation points. Weak convergence of the entire sequence then follows if the minimum is attained. Our analysis unifies and extends several previous results. We then focus on $\ell_1$-regularized optimization, which is the ubiquitous special case where the nonsmooth term is the $\ell_1$-norm. For certain parameter choices, GIPSA is amenable to a local analysis for this problem. For these choices we show that GIPSA achieves finite "active manifold identification", i.e. convergence in a finite number of iterations to the optimal support and sign, after which GIPSA reduces to minimizing a local smooth function. Local linear convergence then holds under certain conditions. We determine the rate in terms of the inertia, stepsize, and local curvature. Our local analysis is applicable to certain recent variants of the Fast Iterative Shrinkage-Thresholding Algorithm (FISTA), for which we establish active manifold identification and local linear convergence. Our analysis motivates the use of a momentum restart scheme in these FISTA variants to obtain the optimal local linear convergence rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge