Density Estimation via Measure Transport: Outlook for Applications in the Biological Sciences

One among several advantages of measure transport methods is that they allow for a unified framework for processing and analysis of data distributed according to a wide class of probability measures. Within this context, we present results from computational studies aimed at assessing the potential of measure transport techniques, specifically, the use of triangular transport maps, as part of a workflow intended to support research in the biological sciences. Scarce data scenarios, which are common in domains such as radiation biology, are of particular interest. We find that when data is scarce, sparse transport maps are advantageous. In particular, statistics gathered from computing series of (sparse) adaptive transport maps, trained on a series of randomly chosen subsets of the set of available data samples, leads to uncovering information hidden in the data. As a result, in the radiation biology application considered here, this approach provides a tool for generating hypotheses about gene relationships and their dynamics under radiation exposure.

Stochastic Projective Splitting: Solving Saddle-Point Problems with Multiple Regularizers

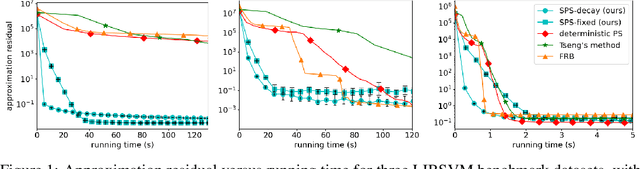
We present a new, stochastic variant of the projective splitting (PS) family of algorithms for monotone inclusion problems. It can solve min-max and noncooperative game formulations arising in applications such as robust ML without the convergence issues associated with gradient descent-ascent, the current de facto standard approach in such situations. Our proposal is the first version of PS able to use stochastic (as opposed to deterministic) gradient oracles. It is also the first stochastic method that can solve min-max games while easily handling multiple constraints and nonsmooth regularizers via projection and proximal operators. We close with numerical experiments on a distributionally robust sparse logistic regression problem.

Single-Forward-Step Projective Splitting: Exploiting Cocoercivity

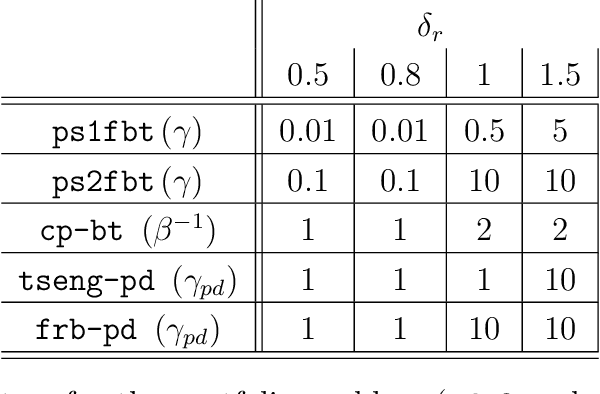
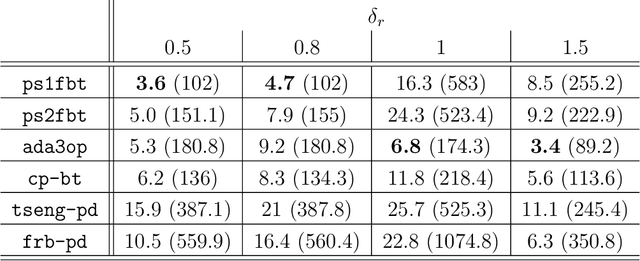
This work describes a new variant of projective splitting in which cocoercive operators can be processed with a single forward step per iteration. This result establishes a symmetry between projective splitting algorithms, the classical forward-backward method, and Tseng's forward-backward-forward method. In a situation in which Lipschitz monotone operators require two forward steps within the projective splitting framework, cocoercive operators may now be processed with just one forward step. Symmetrically, Tseng's method requires two forward steps for a Lipschitz monotone operator and the forward-backward method requires only one for a cocoercive operator. Another symmetry is that the new procedure allows for larger stepsizes for cocoercive operators: bounded by $2\beta$ for a $\beta$-cocoercive operator, which is the same as the forward-backward method. We also develop a backtracking procedure for when the cocoercivity constant is unknown. The single forward step may be interpreted as a single step of the classical gradient method applied to solving the standard resolvent-type update in projective splitting, starting at the previous known point in the operator graph. Proving convergence of the algorithm requires some departures from the usual proof framework for projective splitting.

Projective Splitting with Forward Steps only Requires Continuity

A recent innovation in projective splitting algorithms for monotone operator inclusions has been the development of a procedure using two forward steps instead of the customary proximal steps for operators that are Lipschitz continuous. This paper shows that the Lipschitz assumption is unnecessary when the forward steps are performed in finite-dimensional spaces: a backtracking linesearch yields a convergent algorithm for operators that are merely continuous with full domain.

Convergence Rates for Projective Splitting

Projective splitting is a family of methods for solving inclusions involving sums of maximal monotone operators. First introduced by Eckstein and Svaiter in 2008, these methods have enjoyed significant innovation in recent years, becoming one of the most flexible operator splitting frameworks available. While weak convergence of the iterates to a solution has been established, there have been few attempts to study convergence rates of projective splitting. The purpose of this paper is to do so under various assumptions. To this end, there are three main contributions. First, in the context of convex optimization, we establish an $O(1/k)$ ergodic function convergence rate. Second, for strongly monotone inclusions, strong convergence is established as well as an ergodic $O(1/\sqrt{k})$ convergence rate for the distance of the iterates to the solution. Finally, for inclusions featuring strong monotonicity and cocoercivity, linear convergence is established.

Projective Splitting with Forward Steps: Asynchronous and Block-Iterative Operator Splitting

This work is concerned with the classical problem of finding a zero of a sum of maximal monotone operators. For the projective splitting framework recently proposed by Combettes and Eckstein, we show how to replace the fundamental subproblem calculation using a backward step with one based on two forward steps. The resulting algorithms have the same kind of coordination procedure and can be implemented in the same block-iterative and potentially distributed and asynchronous manner, but may perform backward steps on some operators and forward steps on others. Prior algorithms in the projective splitting family have used only backward steps. Forward steps can be used for any Lipschitz-continuous operators provided the stepsize is bounded by the inverse of the Lipschitz constant. If the Lipschitz constant is unknown, a simple backtracking linesearch procedure may be used. For affine operators, the stepsize can be chosen adaptively without knowledge of the Lipschitz constant and without any additional forward steps. We close the paper by empirically studying the performance of several kinds of splitting algorithms on the lasso problem.

Faster Subgradient Methods for Functions with Hölderian Growth

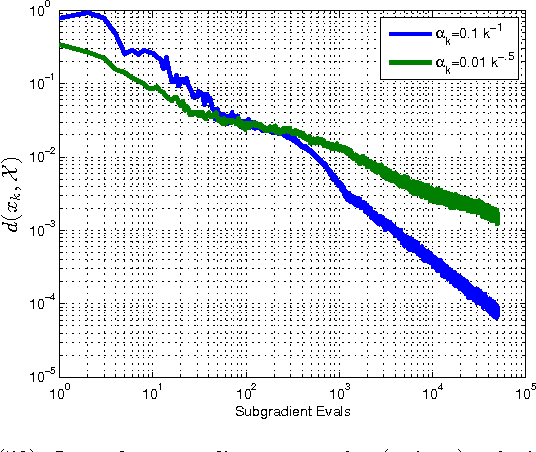
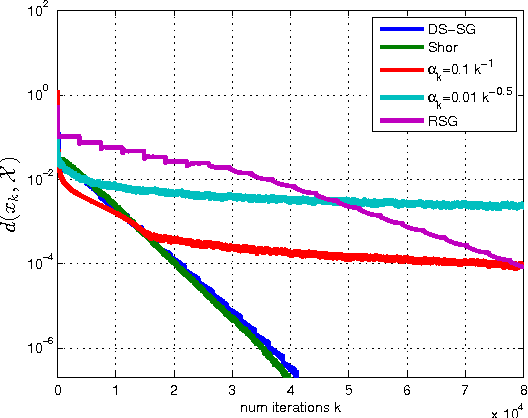
The purpose of this manuscript is to derive new convergence results for several subgradient methods applied to minimizing nonsmooth convex functions with H\"olderian growth. The growth condition is satisfied in many applications and includes functions with quadratic growth and weakly sharp minima as special cases. To this end there are three main contributions. First, for a constant and sufficiently small stepsize, we show that the subgradient method achieves linear convergence up to a certain region including the optimal set, with error of the order of the stepsize. Second, if appropriate problem parameters are known, we derive a decaying stepsize which obtains a much faster convergence rate than is suggested by the classical $O(1/\sqrt{k})$ result for the subgradient method. Thirdly we develop a novel "descending stairs" stepsize which obtains this faster convergence rate and also obtains linear convergence for the special case of weakly sharp functions. We also develop an adaptive variant of the "descending stairs" stepsize which achieves the same convergence rate without requiring an error bound constant which is difficult to estimate in practice.

Local and Global Convergence of a General Inertial Proximal Splitting Scheme

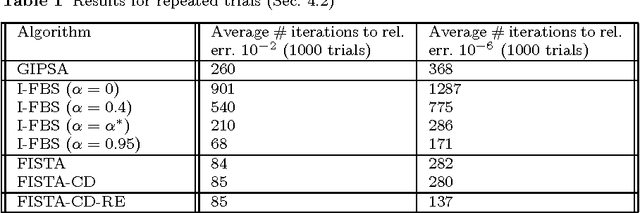
This paper is concerned with convex composite minimization problems in a Hilbert space. In these problems, the objective is the sum of two closed, proper, and convex functions where one is smooth and the other admits a computationally inexpensive proximal operator. We analyze a general family of inertial proximal splitting algorithms (GIPSA) for solving such problems. We establish finiteness of the sum of squared increments of the iterates and optimality of the accumulation points. Weak convergence of the entire sequence then follows if the minimum is attained. Our analysis unifies and extends several previous results. We then focus on $\ell_1$-regularized optimization, which is the ubiquitous special case where the nonsmooth term is the $\ell_1$-norm. For certain parameter choices, GIPSA is amenable to a local analysis for this problem. For these choices we show that GIPSA achieves finite "active manifold identification", i.e. convergence in a finite number of iterations to the optimal support and sign, after which GIPSA reduces to minimizing a local smooth function. Local linear convergence then holds under certain conditions. We determine the rate in terms of the inertia, stepsize, and local curvature. Our local analysis is applicable to certain recent variants of the Fast Iterative Shrinkage-Thresholding Algorithm (FISTA), for which we establish active manifold identification and local linear convergence. Our analysis motivates the use of a momentum restart scheme in these FISTA variants to obtain the optimal local linear convergence rate.