Problem-dependent convergence bounds for randomized linear gradient compression

In distributed optimization, the communication of model updates can be a performance bottleneck. Consequently, gradient compression has been proposed as a means of increasing optimization throughput. In general, due to information loss, compression introduces a penalty on the number of iterations needed to reach a solution. In this work, we investigate how the iteration penalty depends on the interaction between compression and problem structure, in the context of non-convex stochastic optimization. We focus on linear compression schemes, where compression and decompression can be modeled as multiplication with a random matrix. We consider several distributions of matrices, among them random orthogonal matrices and matrices with random Gaussian entries. We find that in each case, the impact of compression on convergence can be quantified in terms of the norm of the Hessian of the objective, using a norm defined by the compression scheme. The analysis reveals that in certain cases, compression performance is related to low-rank structure or other spectral properties of the problem. In these cases, our bounds predict that the penalty introduced by compression is significantly reduced compared to worst-case bounds that only consider the compression level, ignoring problem data. We verify the theoretical findings on several optimization problems, including fine-tuning an image classification model.

An Evaluation of Real-time Adaptive Sampling Change Point Detection Algorithm using KCUSUM

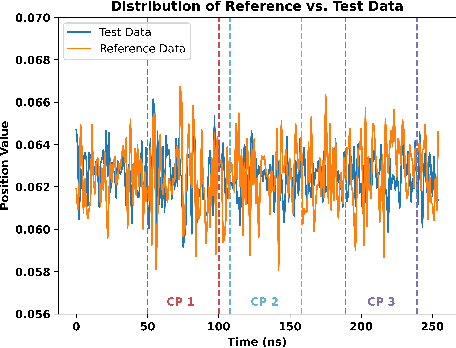
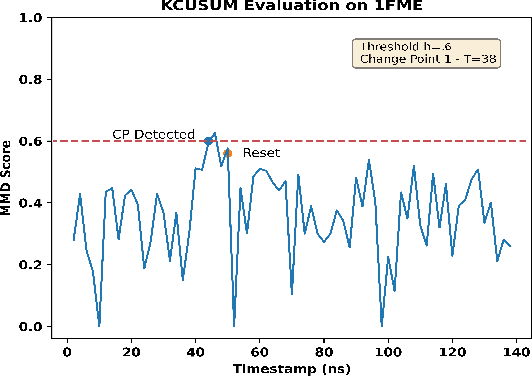
Detecting abrupt changes in real-time data streams from scientific simulations presents a challenging task, demanding the deployment of accurate and efficient algorithms. Identifying change points in live data stream involves continuous scrutiny of incoming observations for deviations in their statistical characteristics, particularly in high-volume data scenarios. Maintaining a balance between sudden change detection and minimizing false alarms is vital. Many existing algorithms for this purpose rely on known probability distributions, limiting their feasibility. In this study, we introduce the Kernel-based Cumulative Sum (KCUSUM) algorithm, a non-parametric extension of the traditional Cumulative Sum (CUSUM) method, which has gained prominence for its efficacy in online change point detection under less restrictive conditions. KCUSUM splits itself by comparing incoming samples directly with reference samples and computes a statistic grounded in the Maximum Mean Discrepancy (MMD) non-parametric framework. This approach extends KCUSUM's pertinence to scenarios where only reference samples are available, such as atomic trajectories of proteins in vacuum, facilitating the detection of deviations from the reference sample without prior knowledge of the data's underlying distribution. Furthermore, by harnessing MMD's inherent random-walk structure, we can theoretically analyze KCUSUM's performance across various use cases, including metrics like expected delay and mean runtime to false alarms. Finally, we discuss real-world use cases from scientific simulations such as NWChem CODAR and protein folding data, demonstrating KCUSUM's practical effectiveness in online change point detection.

Learning Independent Program and Architecture Representations for Generalizable Performance Modeling

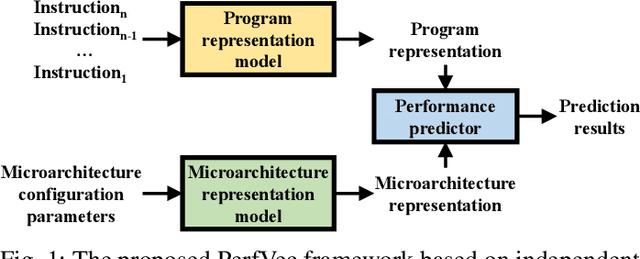
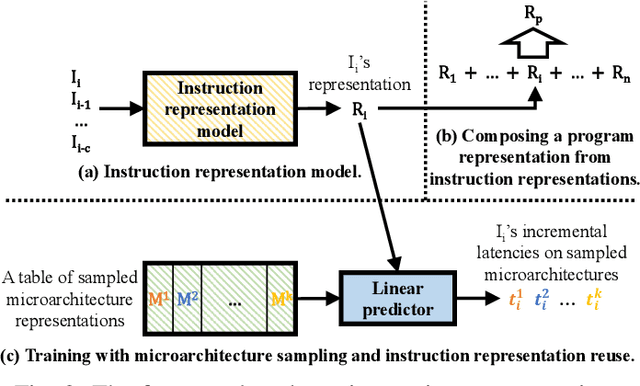
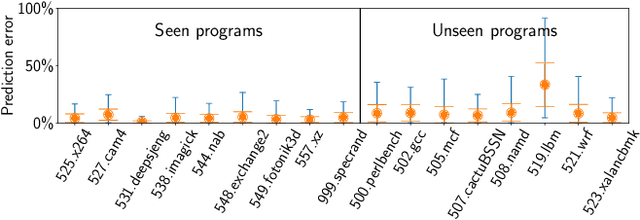
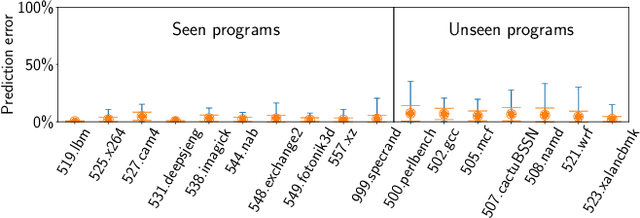
This paper proposes PerfVec, a novel deep learning-based performance modeling framework that learns high-dimensional, independent/orthogonal program and microarchitecture representations. Once learned, a program representation can be used to predict its performance on any microarchitecture, and likewise, a microarchitecture representation can be applied in the performance prediction of any program. Additionally, PerfVec yields a foundation model that captures the performance essence of instructions, which can be directly used by developers in numerous performance modeling related tasks without incurring its training cost. The evaluation demonstrates that PerfVec is more general, efficient, and accurate than previous approaches.

Stochastic Projective Splitting: Solving Saddle-Point Problems with Multiple Regularizers

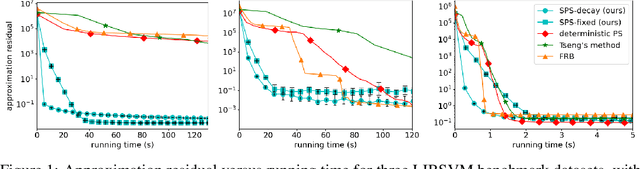
We present a new, stochastic variant of the projective splitting (PS) family of algorithms for monotone inclusion problems. It can solve min-max and noncooperative game formulations arising in applications such as robust ML without the convergence issues associated with gradient descent-ascent, the current de facto standard approach in such situations. Our proposal is the first version of PS able to use stochastic (as opposed to deterministic) gradient oracles. It is also the first stochastic method that can solve min-max games while easily handling multiple constraints and nonsmooth regularizers via projection and proximal operators. We close with numerical experiments on a distributionally robust sparse logistic regression problem.

SimNet: Computer Architecture Simulation using Machine Learning

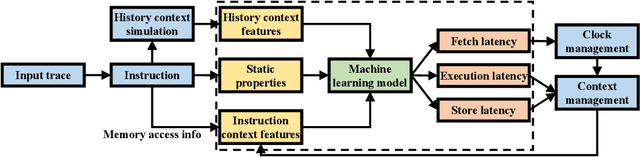
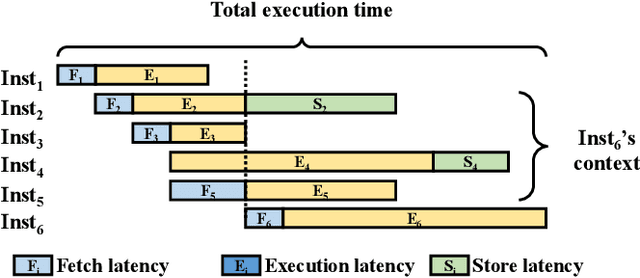
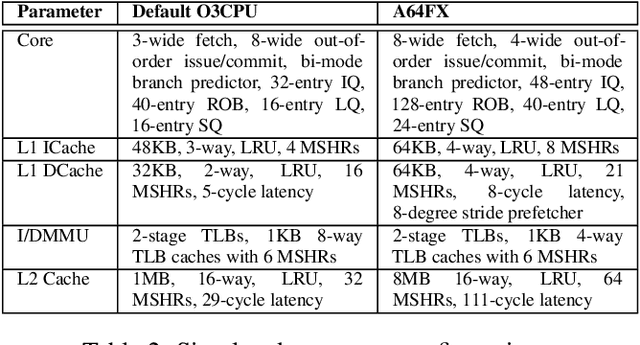
While cycle-accurate simulators are essential tools for architecture research, design, and development, their practicality is limited by an extremely long time-to-solution for realistic problems under investigation. This work describes a concerted effort, where machine learning (ML) is used to accelerate discrete-event simulation. First, an ML-based instruction latency prediction framework that accounts for both static instruction/architecture properties and dynamic execution context is constructed. Then, a GPU-accelerated parallel simulator is implemented based on the proposed instruction latency predictor, and its simulation accuracy and throughput are validated and evaluated against a state-of-the-art simulator. Leveraging modern GPUs, the ML-based simulator outperforms traditional simulators significantly.

Bounding the expected run-time of nonconvex optimization with early stopping

This work examines the convergence of stochastic gradient-based optimization algorithms that use early stopping based on a validation function. The form of early stopping we consider is that optimization terminates when the norm of the gradient of a validation function falls below a threshold. We derive conditions that guarantee this stopping rule is well-defined, and provide bounds on the expected number of iterations and gradient evaluations needed to meet this criterion. The guarantee accounts for the distance between the training and validation sets, measured with the Wasserstein distance. We develop the approach in the general setting of a first-order optimization algorithm, with possibly biased update directions subject to a geometric drift condition. We then derive bounds on the expected running time for early stopping variants of several algorithms, including stochastic gradient descent (SGD), decentralized SGD (DSGD), and the stochastic variance reduced gradient (SVRG) algorithm. Finally, we consider the generalization properties of the iterate returned by early stopping.

Layered SGD: A Decentralized and Synchronous SGD Algorithm for Scalable Deep Neural Network Training

Stochastic Gradient Descent (SGD) is the most popular algorithm for training deep neural networks (DNNs). As larger networks and datasets cause longer training times, training on distributed systems is common and distributed SGD variants, mainly asynchronous and synchronous SGD, are widely used. Asynchronous SGD is communication efficient but suffers from accuracy degradation due to delayed parameter updating. Synchronous SGD becomes communication intensive when the number of nodes increases regardless of its advantage. To address these issues, we introduce Layered SGD (LSGD), a new decentralized synchronous SGD algorithm. LSGD partitions computing resources into subgroups that each contain a communication layer (communicator) and a computation layer (worker). Each subgroup has centralized communication for parameter updates while communication between subgroups is handled by communicators. As a result, communication time is overlapped with I/O latency of workers. The efficiency of the algorithm is tested by training a deep network on the ImageNet classification task.

Gradient Descent using Duality Structures

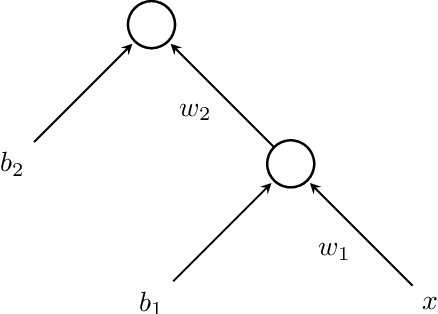
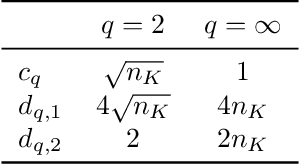
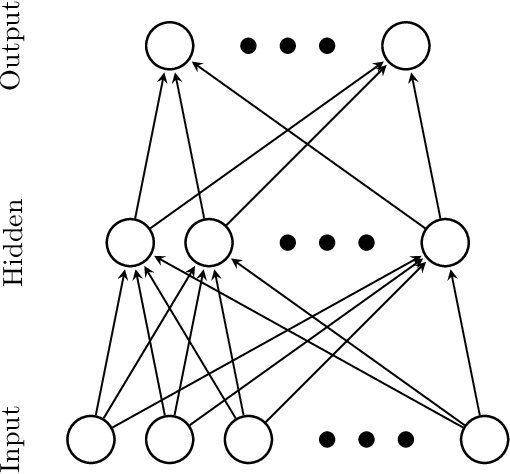
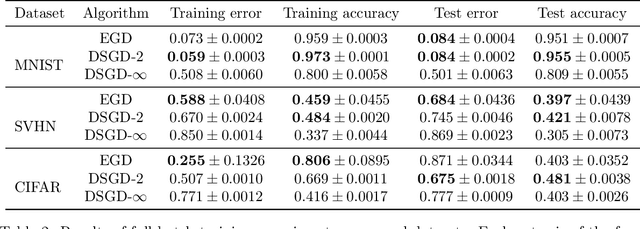
In most applications of gradient-based optimization to complex problems the choice of step size is based on trial-and-error and other heuristics. A case when it is easy to choose the step sizes is when the function has a Lipschitz continuous gradient. Many functions of interest do not appear at first sight to have this property, but often it can be established with the right choice of underlying metric. We find a simple recipe for choosing step sizes when a function has a Lipschitz gradient with respect to any Finsler structure that verifies an exponential bound. These step sizes are guaranteed to give convergence, but they may be conservative since they rely on an exponential bound. However, when relevant problem structure can be encoded in the metric to yield a significantly tighter bound while keeping optimization tractable, this may lead to rigorous and efficient algorithms. In particular, our general result can be applied to yield an optimization algorithm with non-asymptotic performance guarantees for batch optimization of multilayer neural networks.