Gradient Descent using Duality Structures
Paper and Code
Aug 31, 2017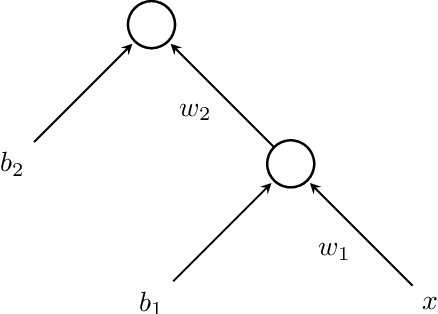
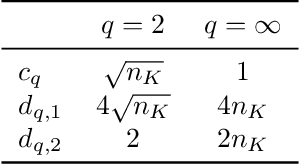
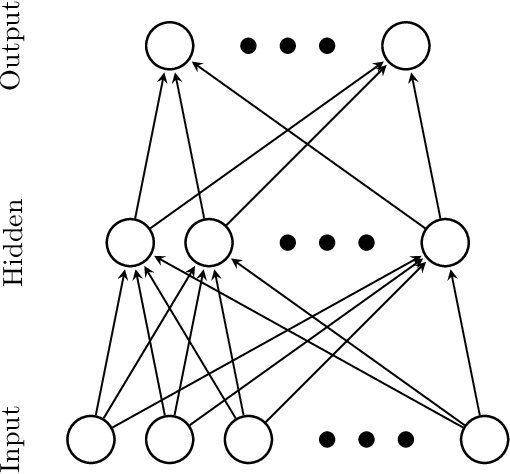
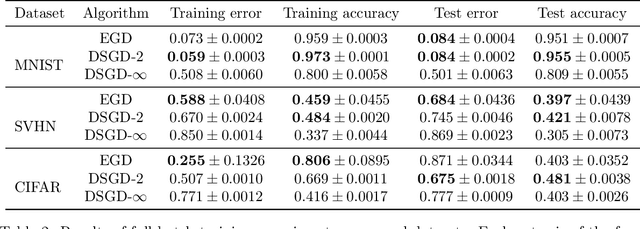
In most applications of gradient-based optimization to complex problems the choice of step size is based on trial-and-error and other heuristics. A case when it is easy to choose the step sizes is when the function has a Lipschitz continuous gradient. Many functions of interest do not appear at first sight to have this property, but often it can be established with the right choice of underlying metric. We find a simple recipe for choosing step sizes when a function has a Lipschitz gradient with respect to any Finsler structure that verifies an exponential bound. These step sizes are guaranteed to give convergence, but they may be conservative since they rely on an exponential bound. However, when relevant problem structure can be encoded in the metric to yield a significantly tighter bound while keeping optimization tractable, this may lead to rigorous and efficient algorithms. In particular, our general result can be applied to yield an optimization algorithm with non-asymptotic performance guarantees for batch optimization of multilayer neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge