Stochastic Projective Splitting: Solving Saddle-Point Problems with Multiple Regularizers
Paper and Code
Jun 24, 2021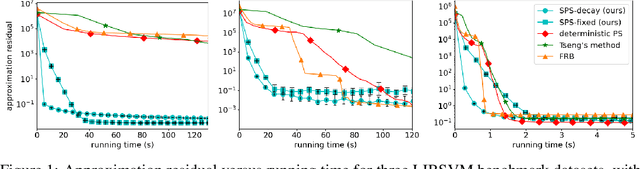
We present a new, stochastic variant of the projective splitting (PS) family of algorithms for monotone inclusion problems. It can solve min-max and noncooperative game formulations arising in applications such as robust ML without the convergence issues associated with gradient descent-ascent, the current de facto standard approach in such situations. Our proposal is the first version of PS able to use stochastic (as opposed to deterministic) gradient oracles. It is also the first stochastic method that can solve min-max games while easily handling multiple constraints and nonsmooth regularizers via projection and proximal operators. We close with numerical experiments on a distributionally robust sparse logistic regression problem.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge