Stochastic Projective Splitting: Solving Saddle-Point Problems with Multiple Regularizers

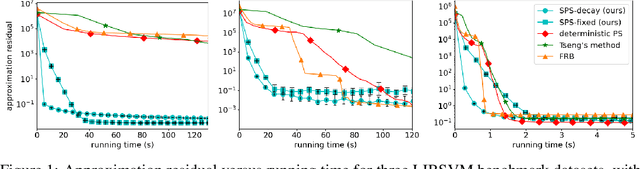
We present a new, stochastic variant of the projective splitting (PS) family of algorithms for monotone inclusion problems. It can solve min-max and noncooperative game formulations arising in applications such as robust ML without the convergence issues associated with gradient descent-ascent, the current de facto standard approach in such situations. Our proposal is the first version of PS able to use stochastic (as opposed to deterministic) gradient oracles. It is also the first stochastic method that can solve min-max games while easily handling multiple constraints and nonsmooth regularizers via projection and proximal operators. We close with numerical experiments on a distributionally robust sparse logistic regression problem.

Single-Forward-Step Projective Splitting: Exploiting Cocoercivity

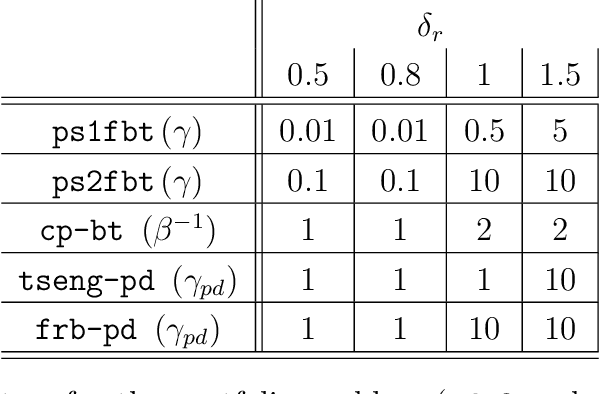
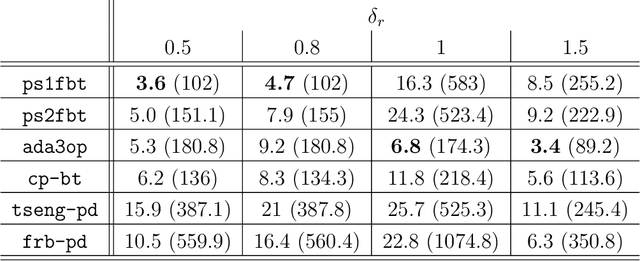
This work describes a new variant of projective splitting in which cocoercive operators can be processed with a single forward step per iteration. This result establishes a symmetry between projective splitting algorithms, the classical forward-backward method, and Tseng's forward-backward-forward method. In a situation in which Lipschitz monotone operators require two forward steps within the projective splitting framework, cocoercive operators may now be processed with just one forward step. Symmetrically, Tseng's method requires two forward steps for a Lipschitz monotone operator and the forward-backward method requires only one for a cocoercive operator. Another symmetry is that the new procedure allows for larger stepsizes for cocoercive operators: bounded by $2\beta$ for a $\beta$-cocoercive operator, which is the same as the forward-backward method. We also develop a backtracking procedure for when the cocoercivity constant is unknown. The single forward step may be interpreted as a single step of the classical gradient method applied to solving the standard resolvent-type update in projective splitting, starting at the previous known point in the operator graph. Proving convergence of the algorithm requires some departures from the usual proof framework for projective splitting.

Projective Splitting with Forward Steps only Requires Continuity

A recent innovation in projective splitting algorithms for monotone operator inclusions has been the development of a procedure using two forward steps instead of the customary proximal steps for operators that are Lipschitz continuous. This paper shows that the Lipschitz assumption is unnecessary when the forward steps are performed in finite-dimensional spaces: a backtracking linesearch yields a convergent algorithm for operators that are merely continuous with full domain.

Convergence Rates for Projective Splitting

Projective splitting is a family of methods for solving inclusions involving sums of maximal monotone operators. First introduced by Eckstein and Svaiter in 2008, these methods have enjoyed significant innovation in recent years, becoming one of the most flexible operator splitting frameworks available. While weak convergence of the iterates to a solution has been established, there have been few attempts to study convergence rates of projective splitting. The purpose of this paper is to do so under various assumptions. To this end, there are three main contributions. First, in the context of convex optimization, we establish an $O(1/k)$ ergodic function convergence rate. Second, for strongly monotone inclusions, strong convergence is established as well as an ergodic $O(1/\sqrt{k})$ convergence rate for the distance of the iterates to the solution. Finally, for inclusions featuring strong monotonicity and cocoercivity, linear convergence is established.

Projective Splitting with Forward Steps: Asynchronous and Block-Iterative Operator Splitting

This work is concerned with the classical problem of finding a zero of a sum of maximal monotone operators. For the projective splitting framework recently proposed by Combettes and Eckstein, we show how to replace the fundamental subproblem calculation using a backward step with one based on two forward steps. The resulting algorithms have the same kind of coordination procedure and can be implemented in the same block-iterative and potentially distributed and asynchronous manner, but may perform backward steps on some operators and forward steps on others. Prior algorithms in the projective splitting family have used only backward steps. Forward steps can be used for any Lipschitz-continuous operators provided the stepsize is bounded by the inverse of the Lipschitz constant. If the Lipschitz constant is unknown, a simple backtracking linesearch procedure may be used. For affine operators, the stepsize can be chosen adaptively without knowledge of the Lipschitz constant and without any additional forward steps. We close the paper by empirically studying the performance of several kinds of splitting algorithms on the lasso problem.