Single-Forward-Step Projective Splitting: Exploiting Cocoercivity

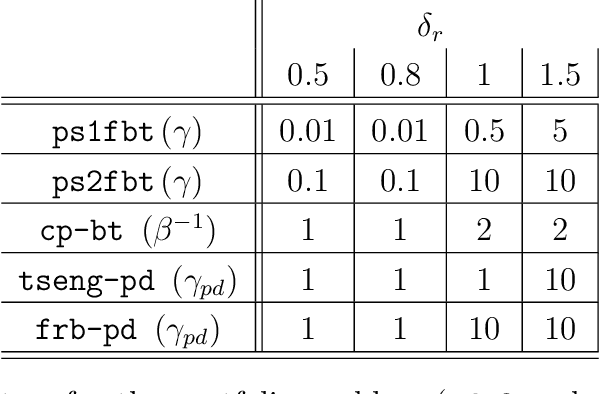
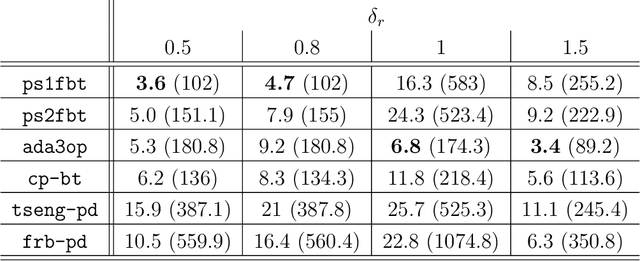
This work describes a new variant of projective splitting in which cocoercive operators can be processed with a single forward step per iteration. This result establishes a symmetry between projective splitting algorithms, the classical forward-backward method, and Tseng's forward-backward-forward method. In a situation in which Lipschitz monotone operators require two forward steps within the projective splitting framework, cocoercive operators may now be processed with just one forward step. Symmetrically, Tseng's method requires two forward steps for a Lipschitz monotone operator and the forward-backward method requires only one for a cocoercive operator. Another symmetry is that the new procedure allows for larger stepsizes for cocoercive operators: bounded by $2\beta$ for a $\beta$-cocoercive operator, which is the same as the forward-backward method. We also develop a backtracking procedure for when the cocoercivity constant is unknown. The single forward step may be interpreted as a single step of the classical gradient method applied to solving the standard resolvent-type update in projective splitting, starting at the previous known point in the operator graph. Proving convergence of the algorithm requires some departures from the usual proof framework for projective splitting.