Robust Machine Learning via Privacy/Rate-Distortion Theory

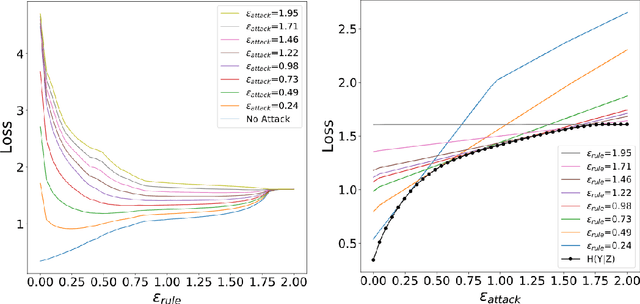
Robust machine learning formulations have emerged to address the prevalent vulnerability of deep neural networks to adversarial examples. Our work draws the connection between optimal robust learning and the privacy-utility tradeoff problem, which is a generalization of the rate-distortion problem. The saddle point of the game between a robust classifier and an adversarial perturbation can be found via the solution of a maximum conditional entropy problem. This information-theoretic perspective sheds light on the fundamental tradeoff between robustness and clean data performance, which ultimately arises from the geometric structure of the underlying data distribution and perturbation constraints. Further, we show that under mild conditions, the worst case adversarial distribution with Wasserstein-ball constraints on the perturbation has a fixed point characterization. This is obtained via the first order necessary conditions for optimality of the derived maximum conditional entropy problem. This fixed point characterization exposes the interplay between the geometry of the ground cost in the Wasserstein-ball constraint, the worst-case adversarial distribution, and the given reference data distribution.