On the Ability of LLMs to Handle Character-Level Perturbations: How Well and How?

This work investigates the resilience of contemporary LLMs against frequent and structured character-level perturbations, specifically through the insertion of noisy characters after each input character. We introduce \nameshort{}, a practical method that inserts invisible Unicode control characters into text to discourage LLM misuse in scenarios such as online exam systems. Surprisingly, despite strong obfuscation that fragments tokenization and reduces the signal-to-noise ratio significantly, many LLMs still maintain notable performance. Through comprehensive evaluation across model-, problem-, and noise-related configurations, we examine the extent and mechanisms of this robustness, exploring both the handling of character-level tokenization and \textit{implicit} versus \textit{explicit} denoising mechanism hypotheses of character-level noises. We hope our findings on the low-level robustness of LLMs will shed light on the risks of their misuse and on the reliability of deploying LLMs across diverse applications.

Pyramidal Flow Matching for Efficient Video Generative Modeling

Video generation requires modeling a vast spatiotemporal space, which demands significant computational resources and data usage. To reduce the complexity, the prevailing approaches employ a cascaded architecture to avoid direct training with full resolution. Despite reducing computational demands, the separate optimization of each sub-stage hinders knowledge sharing and sacrifices flexibility. This work introduces a unified pyramidal flow matching algorithm. It reinterprets the original denoising trajectory as a series of pyramid stages, where only the final stage operates at the full resolution, thereby enabling more efficient video generative modeling. Through our sophisticated design, the flows of different pyramid stages can be interlinked to maintain continuity. Moreover, we craft autoregressive video generation with a temporal pyramid to compress the full-resolution history. The entire framework can be optimized in an end-to-end manner and with a single unified Diffusion Transformer (DiT). Extensive experiments demonstrate that our method supports generating high-quality 5-second (up to 10-second) videos at 768p resolution and 24 FPS within 20.7k A100 GPU training hours. All code and models will be open-sourced at https://pyramid-flow.github.io.

TFLEX: Temporal Feature-Logic Embedding Framework for Complex Reasoning over Temporal Knowledge Graph

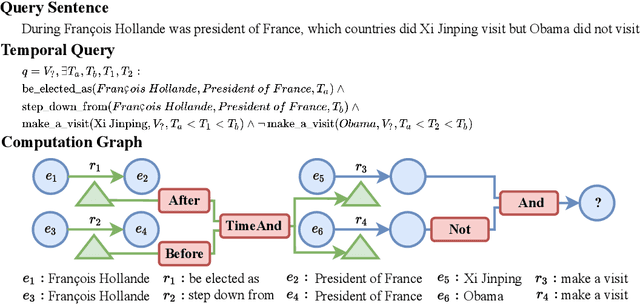
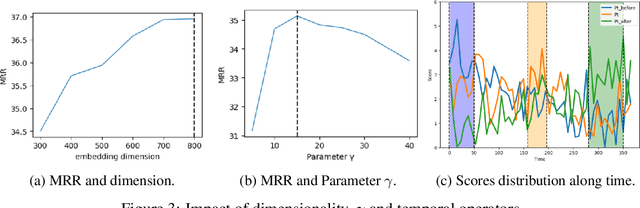
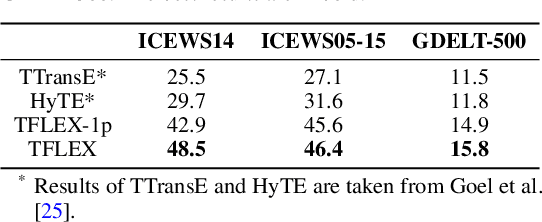
Multi-hop logical reasoning over knowledge graph (KG) plays a fundamental role in many artificial intelligence tasks. Recent complex query embedding (CQE) methods for reasoning focus on static KGs, while temporal knowledge graphs (TKGs) have not been fully explored. Reasoning over TKGs has two challenges: 1. The query should answer entities or timestamps; 2. The operators should consider both set logic on entity set and temporal logic on timestamp set. To bridge this gap, we define the multi-hop logical reasoning problem on TKGs. With generated three datasets, we propose the first temporal CQE named Temporal Feature-Logic Embedding framework (TFLEX) to answer the temporal complex queries. We utilize vector logic to compute the logic part of Temporal Feature-Logic embeddings, thus naturally modeling all First-Order Logic (FOL) operations on entity set. In addition, our framework extends vector logic on timestamp set to cope with three extra temporal operators (After, Before and Between). Experiments on numerous query patterns demonstrate the effectiveness of our method.

Characterizing Parametric and Convergence Stability in Nonconvex and Nonsmooth Optimizations: A Geometric Approach

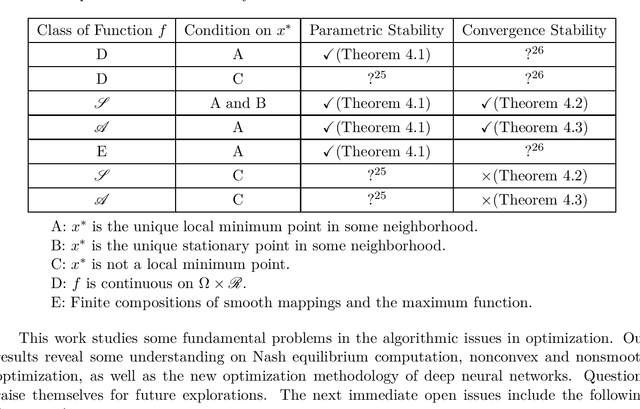
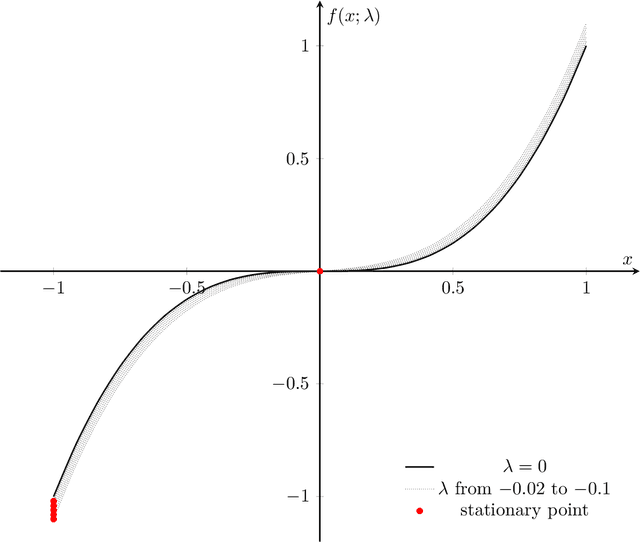
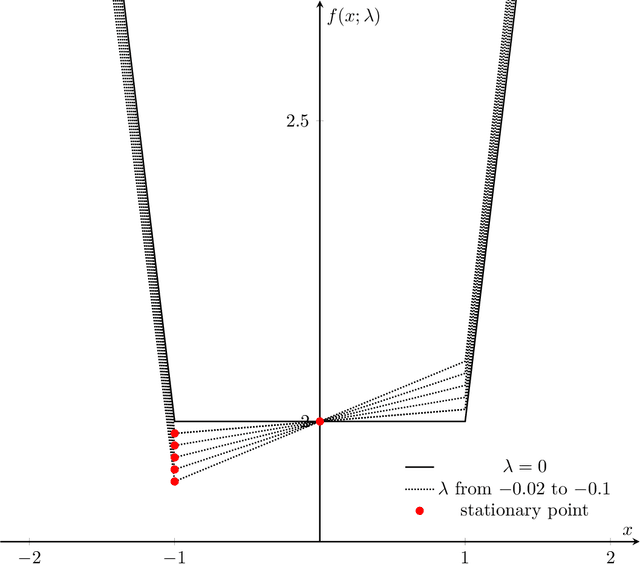
We consider stability issues in minimizing a continuous (probably parameterized, nonconvex and nonsmooth) real-valued function $f$. We call a point stationary if all its possible directional derivatives are nonnegative. In this work, we focus on two notions of stability on stationary points of $f$: parametric stability and convergence stability. Parametric considerations are widely studied in various fields, including smoothed analysis, numerical stability, condition numbers and sensitivity analysis for linear programming. Parametric stability asks whether minor perturbations on parameters lead to dramatic changes in the position and $f$ value of a stationary point. Meanwhile, convergence stability indicates a non-escapable solution: Any point sequence iteratively produced by an optimization algorithm cannot escape from a neighborhood of a stationary point but gets close to it in the sense that such stationary points are stable to the precision parameter and algorithmic numerical errors. It turns out that these notions have deep connections to geometry theory. We show that parametric stability is linked to deformations of graphs of functions. On the other hand, convergence stability is concerned with area partitioning of the function domain. Utilizing these connections, we prove quite tight conditions of these two stability notions for a wide range of functions and optimization algorithms with small enough step sizes and precision parameters. These conditions are subtle in the sense that a slightly weaker function requirement goes to the opposite of primitive intuitions and leads to wrong conclusions. We present three applications of this theory. These applications reveal some understanding on Nash equilibrium computation, nonconvex and nonsmooth optimization, as well as the new optimization methodology of deep neural networks.