Characterizing Parametric and Convergence Stability in Nonconvex and Nonsmooth Optimizations: A Geometric Approach
Paper and Code
Apr 04, 2022
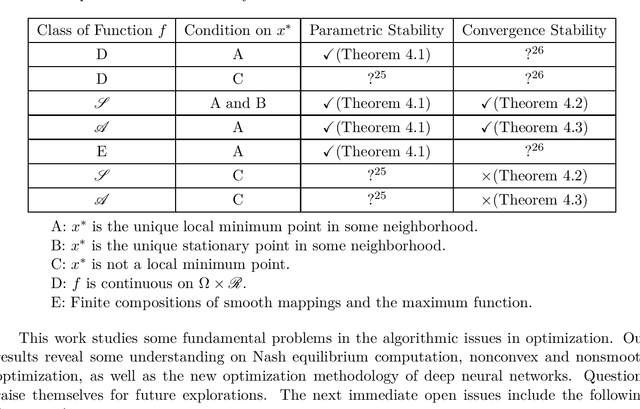
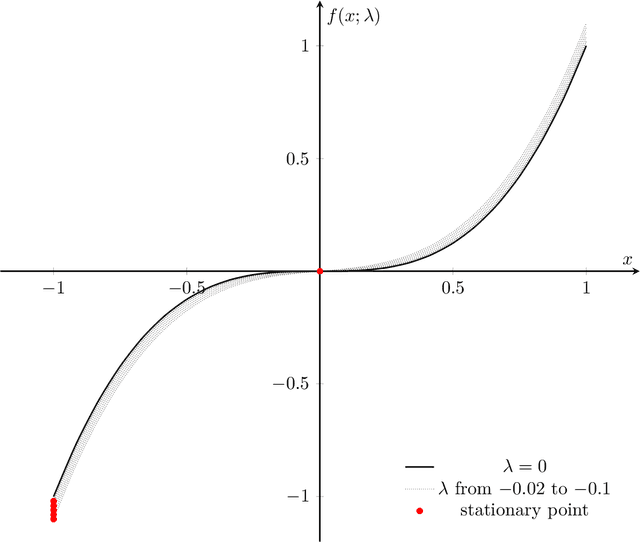
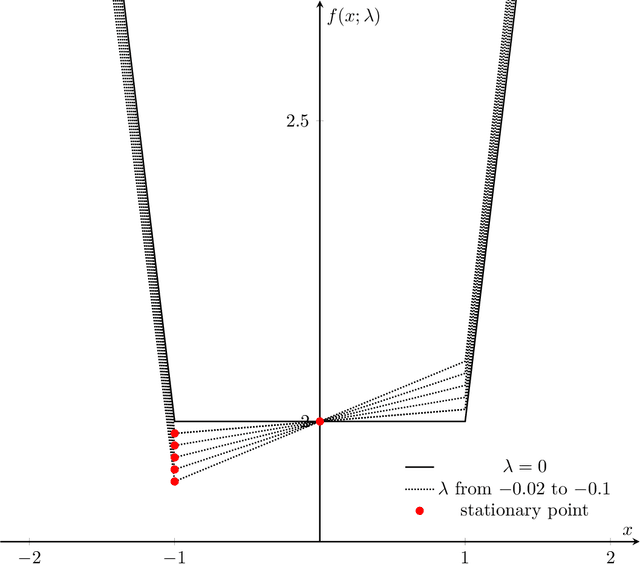
We consider stability issues in minimizing a continuous (probably parameterized, nonconvex and nonsmooth) real-valued function $f$. We call a point stationary if all its possible directional derivatives are nonnegative. In this work, we focus on two notions of stability on stationary points of $f$: parametric stability and convergence stability. Parametric considerations are widely studied in various fields, including smoothed analysis, numerical stability, condition numbers and sensitivity analysis for linear programming. Parametric stability asks whether minor perturbations on parameters lead to dramatic changes in the position and $f$ value of a stationary point. Meanwhile, convergence stability indicates a non-escapable solution: Any point sequence iteratively produced by an optimization algorithm cannot escape from a neighborhood of a stationary point but gets close to it in the sense that such stationary points are stable to the precision parameter and algorithmic numerical errors. It turns out that these notions have deep connections to geometry theory. We show that parametric stability is linked to deformations of graphs of functions. On the other hand, convergence stability is concerned with area partitioning of the function domain. Utilizing these connections, we prove quite tight conditions of these two stability notions for a wide range of functions and optimization algorithms with small enough step sizes and precision parameters. These conditions are subtle in the sense that a slightly weaker function requirement goes to the opposite of primitive intuitions and leads to wrong conclusions. We present three applications of this theory. These applications reveal some understanding on Nash equilibrium computation, nonconvex and nonsmooth optimization, as well as the new optimization methodology of deep neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge