Correct-N-Contrast: A Contrastive Approach for Improving Robustness to Spurious Correlations

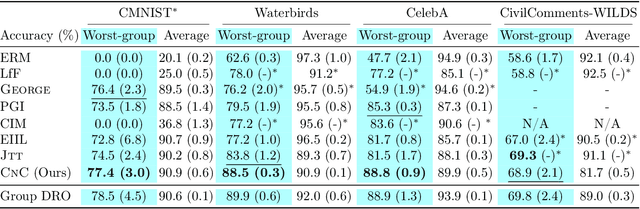
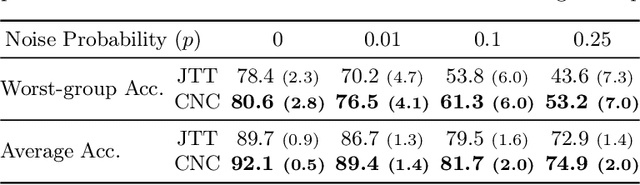
Spurious correlations pose a major challenge for robust machine learning. Models trained with empirical risk minimization (ERM) may learn to rely on correlations between class labels and spurious attributes, leading to poor performance on data groups without these correlations. This is particularly challenging to address when spurious attribute labels are unavailable. To improve worst-group performance on spuriously correlated data without training attribute labels, we propose Correct-N-Contrast (CNC), a contrastive approach to directly learn representations robust to spurious correlations. As ERM models can be good spurious attribute predictors, CNC works by (1) using a trained ERM model's outputs to identify samples with the same class but dissimilar spurious features, and (2) training a robust model with contrastive learning to learn similar representations for same-class samples. To support CNC, we introduce new connections between worst-group error and a representation alignment loss that CNC aims to minimize. We empirically observe that worst-group error closely tracks with alignment loss, and prove that the alignment loss over a class helps upper-bound the class's worst-group vs. average error gap. On popular benchmarks, CNC reduces alignment loss drastically, and achieves state-of-the-art worst-group accuracy by 3.6% average absolute lift. CNC is also competitive with oracle methods that require group labels.

Low-Shot Validation: Active Importance Sampling for Estimating Classifier Performance on Rare Categories

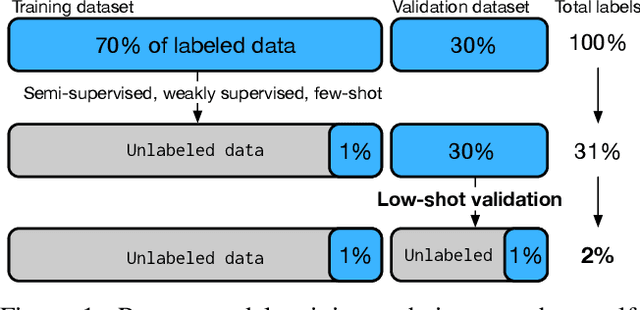
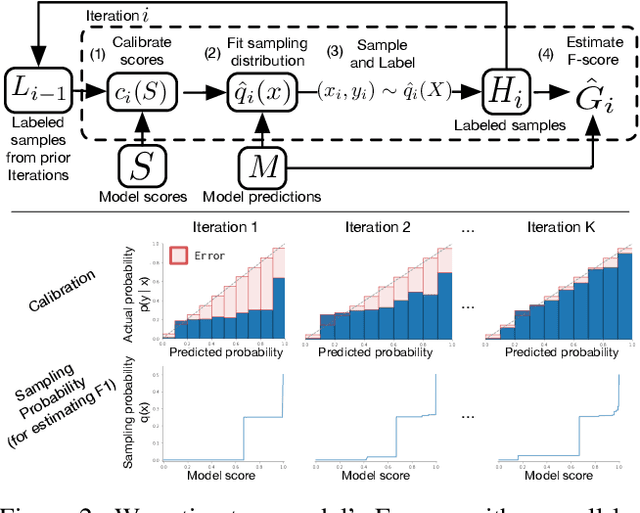
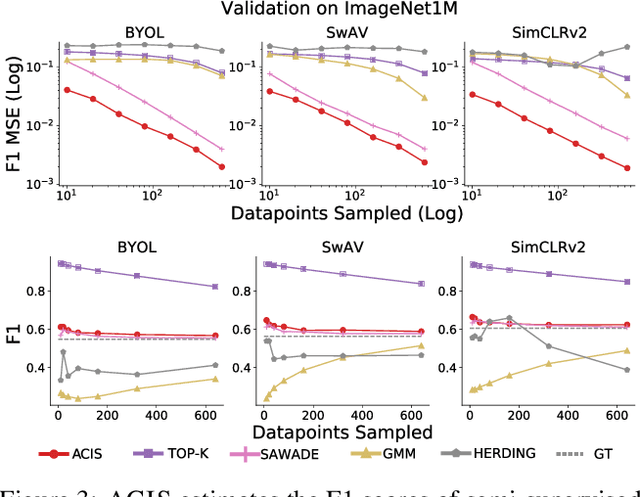
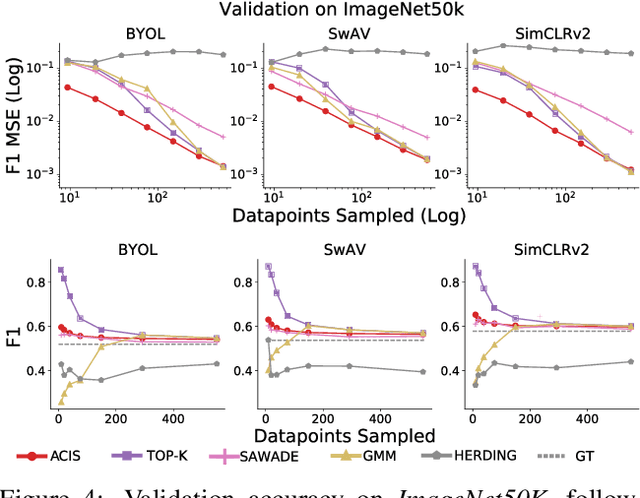
For machine learning models trained with limited labeled training data, validation stands to become the main bottleneck to reducing overall annotation costs. We propose a statistical validation algorithm that accurately estimates the F-score of binary classifiers for rare categories, where finding relevant examples to evaluate on is particularly challenging. Our key insight is that simultaneous calibration and importance sampling enables accurate estimates even in the low-sample regime (< 300 samples). Critically, we also derive an accurate single-trial estimator of the variance of our method and demonstrate that this estimator is empirically accurate at low sample counts, enabling a practitioner to know how well they can trust a given low-sample estimate. When validating state-of-the-art semi-supervised models on ImageNet and iNaturalist2017, our method achieves the same estimates of model performance with up to 10x fewer labels than competing approaches. In particular, we can estimate model F1 scores with a variance of 0.005 using as few as 100 labels.

Kaleidoscope: An Efficient, Learnable Representation For All Structured Linear Maps

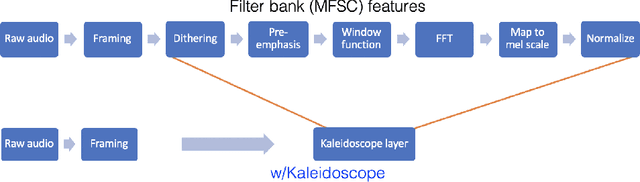
Modern neural network architectures use structured linear transformations, such as low-rank matrices, sparse matrices, permutations, and the Fourier transform, to improve inference speed and reduce memory usage compared to general linear maps. However, choosing which of the myriad structured transformations to use (and its associated parameterization) is a laborious task that requires trading off speed, space, and accuracy. We consider a different approach: we introduce a family of matrices called kaleidoscope matrices (K-matrices) that provably capture any structured matrix with near-optimal space (parameter) and time (arithmetic operation) complexity. We empirically validate that K-matrices can be automatically learned within end-to-end pipelines to replace hand-crafted procedures, in order to improve model quality. For example, replacing channel shuffles in ShuffleNet improves classification accuracy on ImageNet by up to 5%. K-matrices can also simplify hand-engineered pipelines -- we replace filter bank feature computation in speech data preprocessing with a learnable kaleidoscope layer, resulting in only 0.4% loss in accuracy on the TIMIT speech recognition task. In addition, K-matrices can capture latent structure in models: for a challenging permuted image classification task, a K-matrix based representation of permutations is able to learn the right latent structure and improves accuracy of a downstream convolutional model by over 9%. We provide a practically efficient implementation of our approach, and use K-matrices in a Transformer network to attain 36% faster end-to-end inference speed on a language translation task.

No Subclass Left Behind: Fine-Grained Robustness in Coarse-Grained Classification Problems

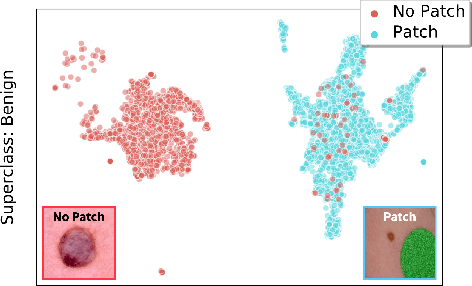
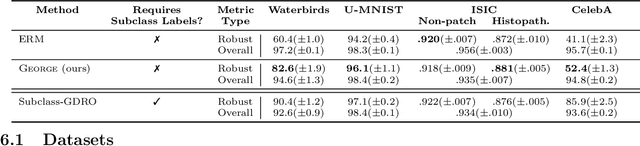
In real-world classification tasks, each class often comprises multiple finer-grained "subclasses." As the subclass labels are frequently unavailable, models trained using only the coarser-grained class labels often exhibit highly variable performance across different subclasses. This phenomenon, known as hidden stratification, has important consequences for models deployed in safety-critical applications such as medicine. We propose GEORGE, a method to both measure and mitigate hidden stratification even when subclass labels are unknown. We first observe that unlabeled subclasses are often separable in the feature space of deep models, and exploit this fact to estimate subclass labels for the training data via clustering techniques. We then use these approximate subclass labels as a form of noisy supervision in a distributionally robust optimization objective. We theoretically characterize the performance of GEORGE in terms of the worst-case generalization error across any subclass. We empirically validate GEORGE on a mix of real-world and benchmark image classification datasets, and show that our approach boosts worst-case subclass accuracy by up to 22 percentage points compared to standard training techniques, without requiring any information about the subclasses.