Kaleidoscope: An Efficient, Learnable Representation For All Structured Linear Maps

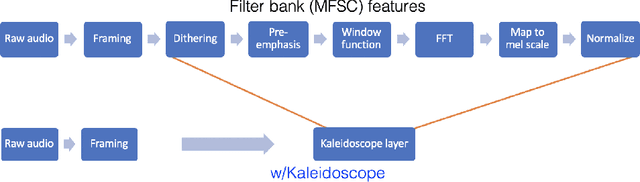
Modern neural network architectures use structured linear transformations, such as low-rank matrices, sparse matrices, permutations, and the Fourier transform, to improve inference speed and reduce memory usage compared to general linear maps. However, choosing which of the myriad structured transformations to use (and its associated parameterization) is a laborious task that requires trading off speed, space, and accuracy. We consider a different approach: we introduce a family of matrices called kaleidoscope matrices (K-matrices) that provably capture any structured matrix with near-optimal space (parameter) and time (arithmetic operation) complexity. We empirically validate that K-matrices can be automatically learned within end-to-end pipelines to replace hand-crafted procedures, in order to improve model quality. For example, replacing channel shuffles in ShuffleNet improves classification accuracy on ImageNet by up to 5%. K-matrices can also simplify hand-engineered pipelines -- we replace filter bank feature computation in speech data preprocessing with a learnable kaleidoscope layer, resulting in only 0.4% loss in accuracy on the TIMIT speech recognition task. In addition, K-matrices can capture latent structure in models: for a challenging permuted image classification task, a K-matrix based representation of permutations is able to learn the right latent structure and improves accuracy of a downstream convolutional model by over 9%. We provide a practically efficient implementation of our approach, and use K-matrices in a Transformer network to attain 36% faster end-to-end inference speed on a language translation task.

Learning Fast Algorithms for Linear Transforms Using Butterfly Factorizations

Fast linear transforms are ubiquitous in machine learning, including the discrete Fourier transform, discrete cosine transform, and other structured transformations such as convolutions. All of these transforms can be represented by dense matrix-vector multiplication, yet each has a specialized and highly efficient (subquadratic) algorithm. We ask to what extent hand-crafting these algorithms and implementations is necessary, what structural priors they encode, and how much knowledge is required to automatically learn a fast algorithm for a provided structured transform. Motivated by a characterization of fast matrix-vector multiplication as products of sparse matrices, we introduce a parameterization of divide-and-conquer methods that is capable of representing a large class of transforms. This generic formulation can automatically learn an efficient algorithm for many important transforms; for example, it recovers the $O(N \log N)$ Cooley-Tukey FFT algorithm to machine precision, for dimensions $N$ up to $1024$. Furthermore, our method can be incorporated as a lightweight replacement of generic matrices in machine learning pipelines to learn efficient and compressible transformations. On a standard task of compressing a single hidden-layer network, our method exceeds the classification accuracy of unconstrained matrices on CIFAR-10 by 3.9 points---the first time a structured approach has done so---with 4X faster inference speed and 40X fewer parameters.

Fast Counting in Machine Learning Applications

We propose scalable methods to execute counting queries in machine learning applications. To achieve memory and computational efficiency, we abstract counting queries and their context such that the counts can be aggregated as a stream. We demonstrate performance and scalability of the resulting approach on random queries, and through extensive experimentation using Bayesian networks learning and association rule mining. Our methods significantly outperform commonly used ADtrees and hash tables, and are practical alternatives for processing large-scale data.