AutoMixer for Improved Multivariate Time-Series Forecasting on Business and IT Observability Data

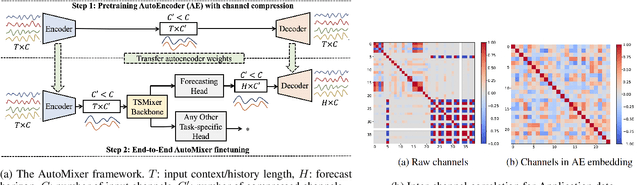
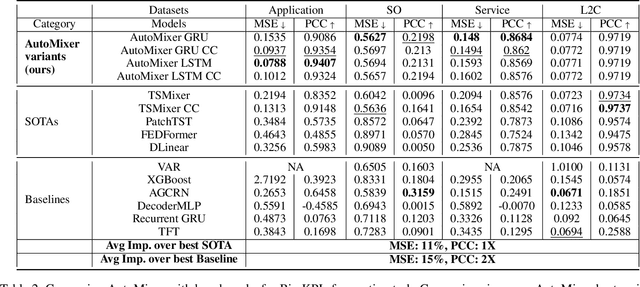
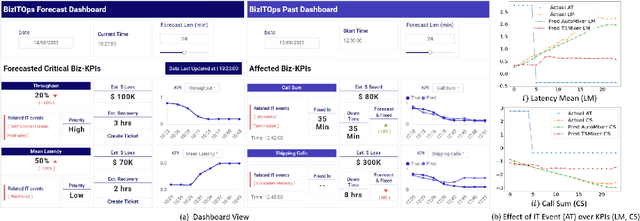
The efficiency of business processes relies on business key performance indicators (Biz-KPIs), that can be negatively impacted by IT failures. Business and IT Observability (BizITObs) data fuses both Biz-KPIs and IT event channels together as multivariate time series data. Forecasting Biz-KPIs in advance can enhance efficiency and revenue through proactive corrective measures. However, BizITObs data generally exhibit both useful and noisy inter-channel interactions between Biz-KPIs and IT events that need to be effectively decoupled. This leads to suboptimal forecasting performance when existing multivariate forecasting models are employed. To address this, we introduce AutoMixer, a time-series Foundation Model (FM) approach, grounded on the novel technique of channel-compressed pretrain and finetune workflows. AutoMixer leverages an AutoEncoder for channel-compressed pretraining and integrates it with the advanced TSMixer model for multivariate time series forecasting. This fusion greatly enhances the potency of TSMixer for accurate forecasts and also generalizes well across several downstream tasks. Through detailed experiments and dashboard analytics, we show AutoMixer's capability to consistently improve the Biz-KPI's forecasting accuracy (by 11-15\%) which directly translates to actionable business insights.

Multi-Agent congestion cost minimization with linear function approximation

This work considers multiple agents traversing a network from a source node to the goal node. The cost to an agent for traveling a link has a private as well as a congestion component. The agent's objective is to find a path to the goal node with minimum overall cost in a decentralized way. We model this as a fully decentralized multi-agent reinforcement learning problem and propose a novel multi-agent congestion cost minimization (MACCM) algorithm. Our MACCM algorithm uses linear function approximations of transition probabilities and the global cost function. In the absence of a central controller and to preserve privacy, agents communicate the cost function parameters to their neighbors via a time-varying communication network. Moreover, each agent maintains its estimate of the global state-action value, which is updated via a multi-agent extended value iteration (MAEVI) sub-routine. We show that our MACCM algorithm achieves a sub-linear regret. The proof requires the convergence of cost function parameters, the MAEVI algorithm, and analysis of the regret bounds induced by the MAEVI triggering condition for each agent. We implement our algorithm on a two node network with multiple links to validate it. We first identify the optimal policy, the optimal number of agents going to the goal node in each period. We observe that the average regret is close to zero for 2 and 3 agents. The optimal policy captures the trade-off between the minimum cost of staying at a node and the congestion cost of going to the goal node. Our work is a generalization of learning the stochastic shortest path problem.

Anomaly Detection using Capsule Networks for High-dimensional Datasets

Anomaly detection is an essential problem in machine learning. Application areas include network security, health care, fraud detection, etc., involving high-dimensional datasets. A typical anomaly detection system always faces the class-imbalance problem in the form of a vast difference in the sample sizes of different classes. They usually have class overlap problems. This study used a capsule network for the anomaly detection task. To the best of our knowledge, this is the first instance where a capsule network is analyzed for the anomaly detection task in a high-dimensional complex data setting. We also handle the related novelty and outlier detection problems. The architecture of the capsule network was suitably modified for a binary classification task. Capsule networks offer a good option for detecting anomalies due to the effect of viewpoint invariance captured in its predictions and viewpoint equivariance captured in internal capsule architecture. We used six-layered under-complete autoencoder architecture with second and third layers containing capsules. The capsules were trained using the dynamic routing algorithm. We created $10$-imbalanced datasets from the original MNIST dataset and compared the performance of the capsule network with $5$ baseline models. Our leading test set measures are F1-score for minority class and area under the ROC curve. We found that the capsule network outperformed every other baseline model on the anomaly detection task by using only ten epochs for training and without using any other data level and algorithm level approach. Thus, we conclude that capsule networks are excellent in modeling complex high-dimensional imbalanced datasets for the anomaly detection task.

Multi-agent Natural Actor-critic Reinforcement Learning Algorithms

Both single-agent and multi-agent actor-critic algorithms are an important class of Reinforcement Learning algorithms. In this work, we propose three fully decentralized multi-agent natural actor-critic (MAN) algorithms. The agents' objective is to collectively learn a joint policy that maximizes the sum of averaged long-term returns of these agents. In the absence of a central controller, agents communicate the information to their neighbors via a time-varying communication network while preserving privacy. We prove the convergence of all the 3 MAN algorithms to a globally asymptotically stable point of the ODE corresponding to the actor update; these use linear function approximations. We use the Fisher information matrix to obtain the natural gradients. The Fisher information matrix captures the curvature of the Kullback-Leibler (KL) divergence between polices at successive iterates. We also show that the gradient of this KL divergence between policies of successive iterates is proportional to the objective function's gradient. Our MAN algorithms indeed use this \emph{representation} of the objective function's gradient. Under certain conditions on the Fisher information matrix, we prove that at each iterate, the optimal value via MAN algorithms can be better than that of the multi-agent actor-critic (MAAC) algorithm using the standard gradients. To validate the usefulness of our proposed algorithms, we implement all the 3 MAN algorithms on a bi-lane traffic network to reduce the average network congestion. We observe an almost 25% reduction in the average congestion in 2 MAN algorithms; the average congestion in another MAN algorithm is on par with the MAAC algorithm. We also consider a generic 15 agent MARL; the performance of the MAN algorithms is again as good as the MAAC algorithm. We attribute the better performance of the MAN algorithms to their use of the above representation.

Thompson Sampling for Unsupervised Sequential Selection

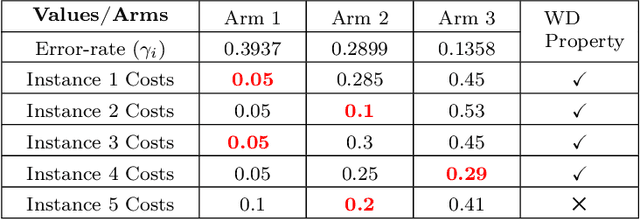
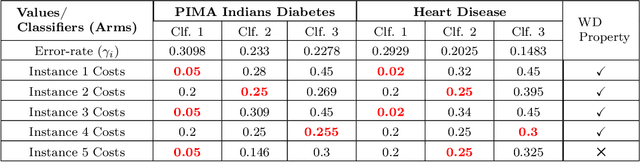
Thompson Sampling has generated significant interest due to its better empirical performance than upper confidence bound based algorithms. In this paper, we study Thompson Sampling based algorithm for Unsupervised Sequential Selection (USS) problem. The USS problem is a variant of the stochastic multi-armed bandits problem, where the loss of an arm can not be inferred from the observed feedback. In the USS setup, arms are associated with fixed costs and are ordered, forming a cascade. In each round, the learner selects an arm and observes the feedback from arms up to the selected arm. The learner's goal is to find the arm that minimizes the expected total loss. The total loss is the sum of the cost incurred for selecting the arm and the stochastic loss associated with the selected arm. The problem is challenging because, without knowing the mean loss, one cannot compute the total loss for the selected arm. Clearly, learning is feasible only if the optimal arm can be inferred from the problem structure. As shown in the prior work, learning is possible when the problem instance satisfies the so-called `Weak Dominance' (WD) property. Under WD, we show that our Thompson Sampling based algorithm for the USS problem achieves near optimal regret and has better numerical performance than existing algorithms.

Optimal Posteriors for Chi-squared Divergence based PAC-Bayesian Bounds and Comparison with KL-divergence based Optimal Posteriors and Cross-Validation Procedure

We investigate optimal posteriors for recently introduced \cite{begin2016pac} chi-squared divergence based PAC-Bayesian bounds in terms of nature of their distribution, scalability of computations, and test set performance. For a finite classifier set, we deduce bounds for three distance functions: KL-divergence, linear and squared distances. Optimal posterior weights are proportional to deviations of empirical risks, usually with subset support. For uniform prior, it is sufficient to search among posteriors on classifier subsets ordered by these risks. We show the bound minimization for linear distance as a convex program and obtain a closed-form expression for its optimal posterior. Whereas that for squared distance is a quasi-convex program under a specific condition, and the one for KL-divergence is non-convex optimization (a difference of convex functions). To compute such optimal posteriors, we derive fast converging fixed point (FP) equations. We apply these approaches to a finite set of SVM regularization parameter values to yield stochastic SVMs with tight bounds. We perform a comprehensive performance comparison between our optimal posteriors and known KL-divergence based posteriors on a variety of UCI datasets with varying ranges and variances in risk values, etc. Chi-squared divergence based posteriors have weaker bounds and worse test errors, hinting at an underlying regularization by KL-divergence based posteriors. Our study highlights the impact of divergence function on the performance of PAC-Bayesian classifiers. We compare our stochastic classifiers with cross-validation based deterministic classifier. The latter has better test errors, but ours is more sample robust, has quantifiable generalization guarantees, and is computationally much faster.

Unsupervised Online Feature Selection for Cost-Sensitive Medical Diagnosis

In medical diagnosis, physicians predict the state of a patient by checking measurements (features) obtained from a sequence of tests, e.g., blood test, urine test, followed by invasive tests. As tests are often costly, one would like to obtain only those features (tests) that can establish the presence or absence of the state conclusively. Another aspect of medical diagnosis is that we are often faced with unsupervised prediction tasks as the true state of the patients may not be known. Motivated by such medical diagnosis problems, we consider a {\it Cost-Sensitive Medical Diagnosis} (CSMD) problem, where the true state of patients is unknown. We formulate the CSMD problem as a feature selection problem where each test gives a feature that can be used in a prediction model. Our objective is to learn strategies for selecting the features that give the best trade-off between accuracy and costs. We exploit the `Weak Dominance' property of problem to develop online algorithms that identify a set of features which provides an `optimal' trade-off between cost and accuracy of prediction without requiring to know the true state of the medical condition. Our empirical results validate the performance of our algorithms on problem instances generated from real-world datasets.

Optimal PAC-Bayesian Posteriors for Stochastic Classifiers and their use for Choice of SVM Regularization Parameter

PAC-Bayesian set up involves a stochastic classifier characterized by a posterior distribution on a classifier set, offers a high probability bound on its averaged true risk and is robust to the training sample used. For a given posterior, this bound captures the trade off between averaged empirical risk and KL-divergence based model complexity term. Our goal is to identify an optimal posterior with the least PAC-Bayesian bound. We consider a finite classifier set and 5 distance functions: KL-divergence, its Pinsker's and a sixth degree polynomial approximations; linear and squared distances. Linear distance based model results in a convex optimization problem. We obtain closed form expression for its optimal posterior. For uniform prior, this posterior has full support with weights negative-exponentially proportional to number of misclassifications. Squared distance and Pinsker's approximation bounds are possibly quasi-convex and are observed to have single local minimum. We derive fixed point equations (FPEs) using partial KKT system with strict positivity constraints. This obviates the combinatorial search for subset support of the optimal posterior. For uniform prior, exponential search on a full-dimensional simplex can be limited to an ordered subset of classifiers with increasing empirical risk values. These FPEs converge rapidly to a stationary point, even for a large classifier set when a solver fails. We apply these approaches to SVMs generated using a finite set of SVM regularization parameter values on 9 UCI datasets. These posteriors yield stochastic SVM classifiers with tight bounds. KL-divergence based bound is the tightest, but is computationally expensive due to non-convexity and multiple calls to a root finding algorithm. Optimal posteriors for all 5 distance functions have lowest 10% test error values on most datasets, with linear distance being the easiest to obtain.