Thompson Sampling for Unsupervised Sequential Selection

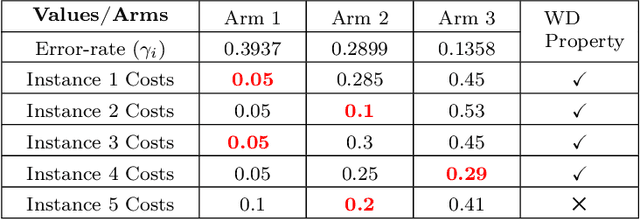
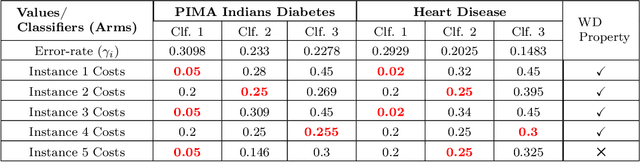
Thompson Sampling has generated significant interest due to its better empirical performance than upper confidence bound based algorithms. In this paper, we study Thompson Sampling based algorithm for Unsupervised Sequential Selection (USS) problem. The USS problem is a variant of the stochastic multi-armed bandits problem, where the loss of an arm can not be inferred from the observed feedback. In the USS setup, arms are associated with fixed costs and are ordered, forming a cascade. In each round, the learner selects an arm and observes the feedback from arms up to the selected arm. The learner's goal is to find the arm that minimizes the expected total loss. The total loss is the sum of the cost incurred for selecting the arm and the stochastic loss associated with the selected arm. The problem is challenging because, without knowing the mean loss, one cannot compute the total loss for the selected arm. Clearly, learning is feasible only if the optimal arm can be inferred from the problem structure. As shown in the prior work, learning is possible when the problem instance satisfies the so-called `Weak Dominance' (WD) property. Under WD, we show that our Thompson Sampling based algorithm for the USS problem achieves near optimal regret and has better numerical performance than existing algorithms.