Diminishing Return of Value Expansion Methods in Model-Based Reinforcement Learning

Model-based reinforcement learning is one approach to increase sample efficiency. However, the accuracy of the dynamics model and the resulting compounding error over modelled trajectories are commonly regarded as key limitations. A natural question to ask is: How much more sample efficiency can be gained by improving the learned dynamics models? Our paper empirically answers this question for the class of model-based value expansion methods in continuous control problems. Value expansion methods should benefit from increased model accuracy by enabling longer rollout horizons and better value function approximations. Our empirical study, which leverages oracle dynamics models to avoid compounding model errors, shows that (1) longer horizons increase sample efficiency, but the gain in improvement decreases with each additional expansion step, and (2) the increased model accuracy only marginally increases the sample efficiency compared to learned models with identical horizons. Therefore, longer horizons and increased model accuracy yield diminishing returns in terms of sample efficiency. These improvements in sample efficiency are particularly disappointing when compared to model-free value expansion methods. Even though they introduce no computational overhead, we find their performance to be on-par with model-based value expansion methods. Therefore, we conclude that the limitation of model-based value expansion methods is not the model accuracy of the learned models. While higher model accuracy is beneficial, our experiments show that even a perfect model will not provide an un-rivalled sample efficiency but that the bottleneck lies elsewhere.

Revisiting Model-based Value Expansion

Model-based value expansion methods promise to improve the quality of value function targets and, thereby, the effectiveness of value function learning. However, to date, these methods are being outperformed by Dyna-style algorithms with conceptually simpler 1-step value function targets. This shows that in practice, the theoretical justification of value expansion does not seem to hold. We provide a thorough empirical study to shed light on the causes of failure of value expansion methods in practice which is believed to be the compounding model error. By leveraging GPU based physics simulators, we are able to efficiently use the true dynamics for analysis inside the model-based reinforcement learning loop. Performing extensive comparisons between true and learned dynamics sheds light into this black box. This paper provides a better understanding of the actual problems in value expansion. We provide future directions of research by empirically testing the maximum theoretical performance of current approaches.

A Differentiable Newton-Euler Algorithm for Real-World Robotics

Obtaining dynamics models is essential for robotics to achieve accurate model-based controllers and simulators for planning. The dynamics models are typically obtained using model specification of the manufacturer or simple numerical methods such as linear regression. However, this approach does not guarantee physically plausible parameters and can only be applied to kinematic chains consisting of rigid bodies. In this article, we describe a differentiable simulator that can be used to identify the system parameters of real-world mechanical systems with complex friction models, holonomic as well as non-holonomic constraints. To guarantee physically consistent parameters, we utilize virtual parameters and gradient-based optimization. The described Differentiable Newton-Euler Algorithm (DiffNEA) can be applied to a class of dynamical systems and guarantees physically plausible predictions. The extensive experimental evaluation shows, that the proposed model learning approach learns accurate dynamics models of systems with complex friction and non-holonomic constraints. Especially in the offline reinforcement learning experiments, the identified DiffNEA models excel. For the challenging ball in a cup task, these models solve the task using model-based offline reinforcement learning on the physical system. The black-box baselines fail on this task in simulation and on the physical system despite using more data for learning the model.

Continuous-Time Fitted Value Iteration for Robust Policies

Solving the Hamilton-Jacobi-Bellman equation is important in many domains including control, robotics and economics. Especially for continuous control, solving this differential equation and its extension the Hamilton-Jacobi-Isaacs equation, is important as it yields the optimal policy that achieves the maximum reward on a give task. In the case of the Hamilton-Jacobi-Isaacs equation, which includes an adversary controlling the environment and minimizing the reward, the obtained policy is also robust to perturbations of the dynamics. In this paper we propose continuous fitted value iteration (cFVI) and robust fitted value iteration (rFVI). These algorithms leverage the non-linear control-affine dynamics and separable state and action reward of many continuous control problems to derive the optimal policy and optimal adversary in closed form. This analytic expression simplifies the differential equations and enables us to solve for the optimal value function using value iteration for continuous actions and states as well as the adversarial case. Notably, the resulting algorithms do not require discretization of states or actions. We apply the resulting algorithms to the Furuta pendulum and cartpole. We show that both algorithms obtain the optimal policy. The robustness Sim2Real experiments on the physical systems show that the policies successfully achieve the task in the real-world. When changing the masses of the pendulum, we observe that robust value iteration is more robust compared to deep reinforcement learning algorithm and the non-robust version of the algorithm. Videos of the experiments are shown at https://sites.google.com/view/rfvi

Combining Physics and Deep Learning to learn Continuous-Time Dynamics Models

Deep learning has been widely used within learning algorithms for robotics. One disadvantage of deep networks is that these networks are black-box representations. Therefore, the learned approximations ignore the existing knowledge of physics or robotics. Especially for learning dynamics models, these black-box models are not desirable as the underlying principles are well understood and the standard deep networks can learn dynamics that violate these principles. To learn dynamics models with deep networks that guarantee physically plausible dynamics, we introduce physics-inspired deep networks that combine first principles from physics with deep learning. We incorporate Lagrangian mechanics within the model learning such that all approximated models adhere to the laws of physics and conserve energy. Deep Lagrangian Networks (DeLaN) parametrize the system energy using two networks. The parameters are obtained by minimizing the squared residual of the Euler-Lagrange differential equation. Therefore, the resulting model does not require specific knowledge of the individual system, is interpretable, and can be used as a forward, inverse, and energy model. Previously these properties were only obtained when using system identification techniques that require knowledge of the kinematic structure. We apply DeLaN to learning dynamics models and apply these models to control simulated and physical rigid body systems. The results show that the proposed approach obtains dynamics models that can be applied to physical systems for real-time control. Compared to standard deep networks, the physics-inspired models learn better models and capture the underlying structure of the dynamics.

Learning Dynamics Models for Model Predictive Agents

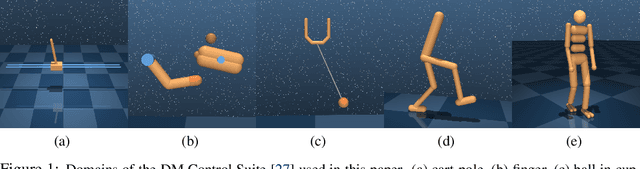
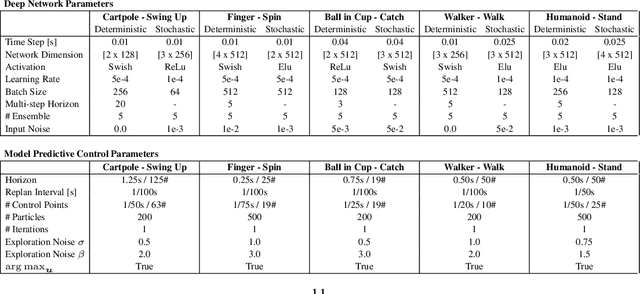
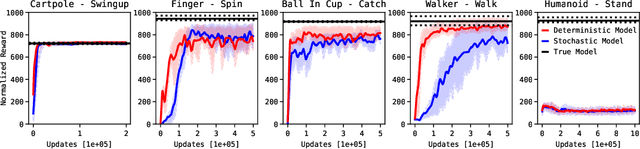
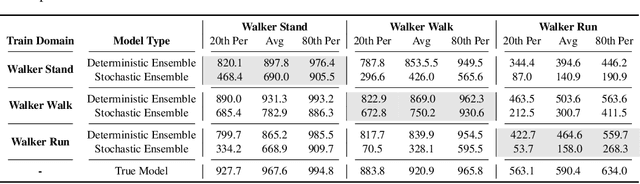
Model-Based Reinforcement Learning involves learning a \textit{dynamics model} from data, and then using this model to optimise behaviour, most often with an online \textit{planner}. Much of the recent research along these lines presents a particular set of design choices, involving problem definition, model learning and planning. Given the multiple contributions, it is difficult to evaluate the effects of each. This paper sets out to disambiguate the role of different design choices for learning dynamics models, by comparing their performance to planning with a ground-truth model -- the simulator. First, we collect a rich dataset from the training sequence of a model-free agent on 5 domains of the DeepMind Control Suite. Second, we train feed-forward dynamics models in a supervised fashion, and evaluate planner performance while varying and analysing different model design choices, including ensembling, stochasticity, multi-step training and timestep size. Besides the quantitative analysis, we describe a set of qualitative findings, rules of thumb, and future research directions for planning with learned dynamics models. Videos of the results are available at https://sites.google.com/view/learning-better-models.

Robust Value Iteration for Continuous Control Tasks

When transferring a control policy from simulation to a physical system, the policy needs to be robust to variations in the dynamics to perform well. Commonly, the optimal policy overfits to the approximate model and the corresponding state-distribution, often resulting in failure to trasnfer underlying distributional shifts. In this paper, we present Robust Fitted Value Iteration, which uses dynamic programming to compute the optimal value function on the compact state domain and incorporates adversarial perturbations of the system dynamics. The adversarial perturbations encourage a optimal policy that is robust to changes in the dynamics. Utilizing the continuous-time perspective of reinforcement learning, we derive the optimal perturbations for the states, actions, observations and model parameters in closed-form. Notably, the resulting algorithm does not require discretization of states or actions. Therefore, the optimal adversarial perturbations can be efficiently incorporated in the min-max value function update. We apply the resulting algorithm to the physical Furuta pendulum and cartpole. By changing the masses of the systems we evaluate the quantitative and qualitative performance across different model parameters. We show that robust value iteration is more robust compared to deep reinforcement learning algorithm and the non-robust version of the algorithm. Videos of the experiments are shown at https://sites.google.com/view/rfvi

Value Iteration in Continuous Actions, States and Time

Classical value iteration approaches are not applicable to environments with continuous states and actions. For such environments, the states and actions are usually discretized, which leads to an exponential increase in computational complexity. In this paper, we propose continuous fitted value iteration (cFVI). This algorithm enables dynamic programming for continuous states and actions with a known dynamics model. Leveraging the continuous-time formulation, the optimal policy can be derived for non-linear control-affine dynamics. This closed-form solution enables the efficient extension of value iteration to continuous environments. We show in non-linear control experiments that the dynamic programming solution obtains the same quantitative performance as deep reinforcement learning methods in simulation but excels when transferred to the physical system. The policy obtained by cFVI is more robust to changes in the dynamics despite using only a deterministic model and without explicitly incorporating robustness in the optimization. Videos of the physical system are available at \url{https://sites.google.com/view/value-iteration}.

Differentiable Physics Models for Real-world Offline Model-based Reinforcement Learning

A limitation of model-based reinforcement learning (MBRL) is the exploitation of errors in the learned models. Black-box models can fit complex dynamics with high fidelity, but their behavior is undefined outside of the data distribution.Physics-based models are better at extrapolating, due to the general validity of their informed structure, but underfit in the real world due to the presence of unmodeled phenomena. In this work, we demonstrate experimentally that for the offline model-based reinforcement learning setting, physics-based models can be beneficial compared to high-capacity function approximators if the mechanical structure is known. Physics-based models can learn to perform the ball in a cup (BiC) task on a physical manipulator using only 4 minutes of sampled data using offline MBRL. We find that black-box models consistently produce unviable policies for BiC as all predicted trajectories diverge to physically impossible state, despite having access to more data than the physics-based model. In addition, we generalize the approach of physics parameter identification from modeling holonomic multi-body systems to systems with nonholonomic dynamics using end-to-end automatic differentiation. Videos: https://sites.google.com/view/ball-in-a-cup-in-4-minutes/

High Acceleration Reinforcement Learning for Real-World Juggling with Binary Rewards

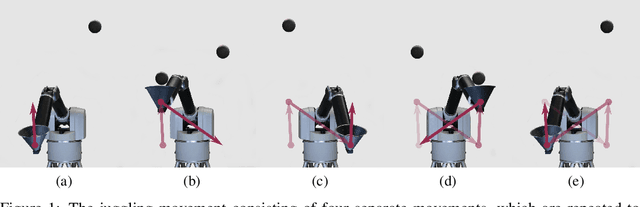
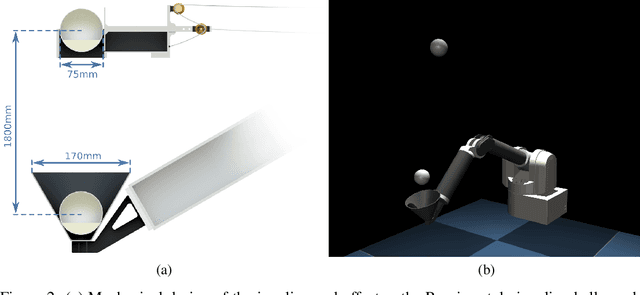
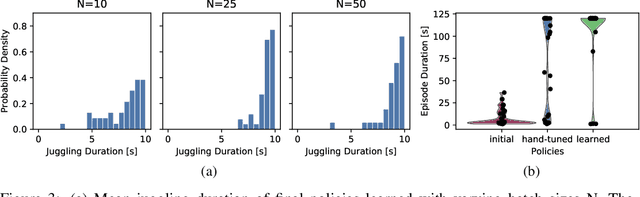
Robots that can learn in the physical world will be important to en-able robots to escape their stiff and pre-programmed movements. For dynamic high-acceleration tasks, such as juggling, learning in the real-world is particularly challenging as one must push the limits of the robot and its actuation without harming the system, amplifying the necessity of sample efficiency and safety for robot learning algorithms. In contrast to prior work which mainly focuses on the learning algorithm, we propose a learning system, that directly incorporates these requirements in the design of the policy representation, initialization, and optimization. We demonstrate that this system enables the high-speed Barrett WAM manipulator to learn juggling two balls from 56 minutes of experience with a binary reward signal. The final policy juggles continuously for up to 33 minutes or about 4500 repeated catches. The videos documenting the learning process and the evaluation can be found at https://sites.google.com/view/jugglingbot