Data-Guided Regulator for Adaptive Nonlinear Control

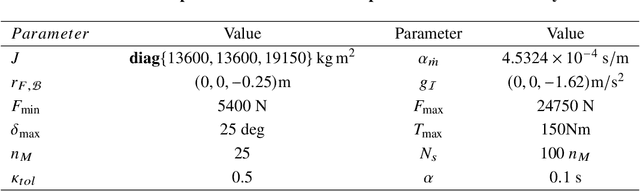
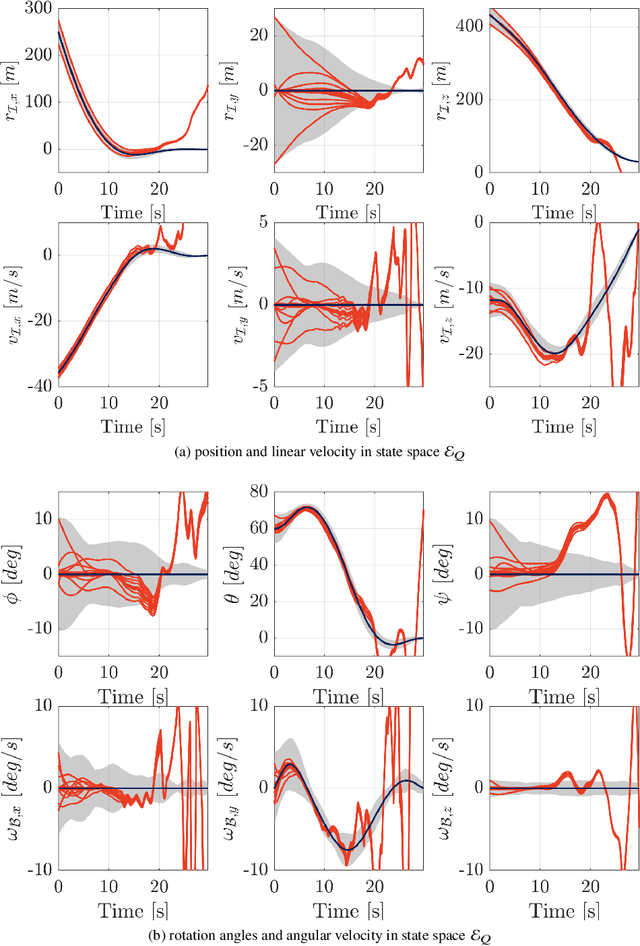
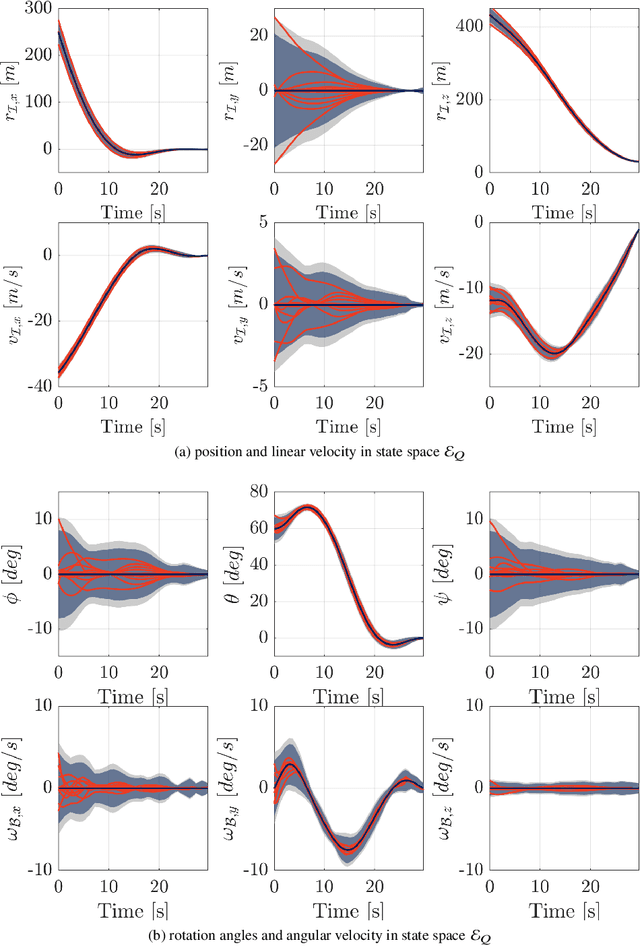
This paper addresses the problem of designing a data-driven feedback controller for complex nonlinear dynamical systems in the presence of time-varying disturbances with unknown dynamics. Such disturbances are modeled as the "unknown" part of the system dynamics. The goal is to achieve finite-time regulation of system states through direct policy updates while also generating informative data that can subsequently be used for data-driven stabilization or system identification. First, we expand upon the notion of "regularizability" and characterize this system characteristic for a linear time-varying representation of the nonlinear system with locally-bounded higher-order terms. "Rapid-regularizability" then gauges the extent by which a system can be regulated in finite time, in contrast to its asymptotic behavior. We then propose the Data-Guided Regulation for Adaptive Nonlinear Control ( DG-RAN) algorithm, an online iterative synthesis procedure that utilizes discrete time-series data from a single trajectory for regulating system states and identifying disturbance dynamics. The effectiveness of our approach is demonstrated on a 6-DOF power descent guidance problem in the presence of adverse environmental disturbances.

Duality-Based Stochastic Policy Optimization for Estimation with Unknown Noise Covariances

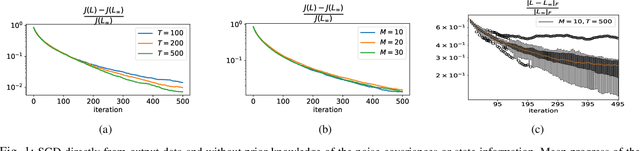
Duality of control and estimation allows mapping recent advances in data-guided control to the estimation setup. This paper formalizes and utilizes such a mapping by considering learning the optimal (steady-state) Kalman gain when process and measurement noise statistics are unknown. Specifically, building on the duality between synthesizing optimal control and estimation gains, the filter design problem is formalized as direct policy learning; subsequently, a Stochastic Gradient Descent (SGD) approach is adopted to learn the optimal filter gain. In this direction, control and estimation duality is also used to extend existing theoretical results for direct policy updates for Linear Quadratic Regulator (LQR) to establish convergence of the proposed algorithm-while addressing subtle differences between the two synthesis problems. The results are illustrated via several numerical examples.

Towards a Theoretical Foundation of Policy Optimization for Learning Control Policies

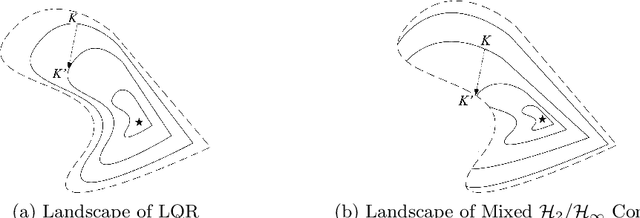
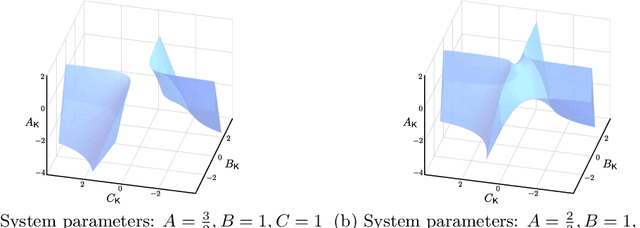
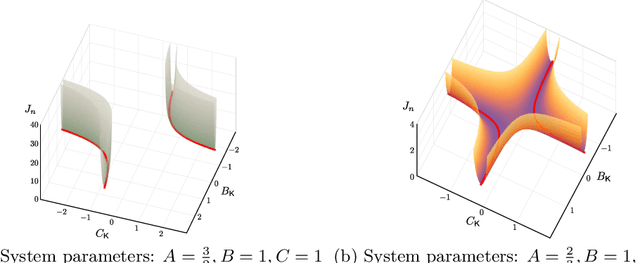
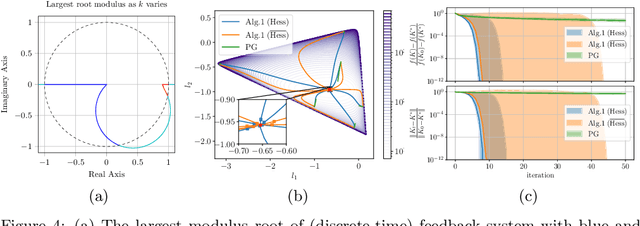
Gradient-based methods have been widely used for system design and optimization in diverse application domains. Recently, there has been a renewed interest in studying theoretical properties of these methods in the context of control and reinforcement learning. This article surveys some of the recent developments on policy optimization, a gradient-based iterative approach for feedback control synthesis, popularized by successes of reinforcement learning. We take an interdisciplinary perspective in our exposition that connects control theory, reinforcement learning, and large-scale optimization. We review a number of recently-developed theoretical results on the optimization landscape, global convergence, and sample complexity of gradient-based methods for various continuous control problems such as the linear quadratic regulator (LQR), $\mathcal{H}_\infty$ control, risk-sensitive control, linear quadratic Gaussian (LQG) control, and output feedback synthesis. In conjunction with these optimization results, we also discuss how direct policy optimization handles stability and robustness concerns in learning-based control, two main desiderata in control engineering. We conclude the survey by pointing out several challenges and opportunities at the intersection of learning and control.

Adaptive Traffic Control with Deep Reinforcement Learning: Towards State-of-the-art and Beyond

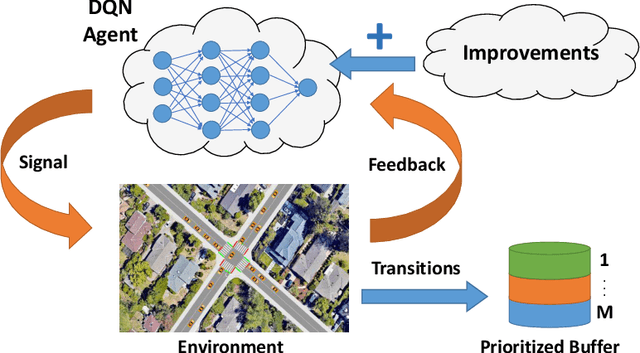
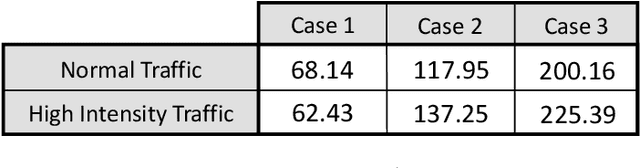
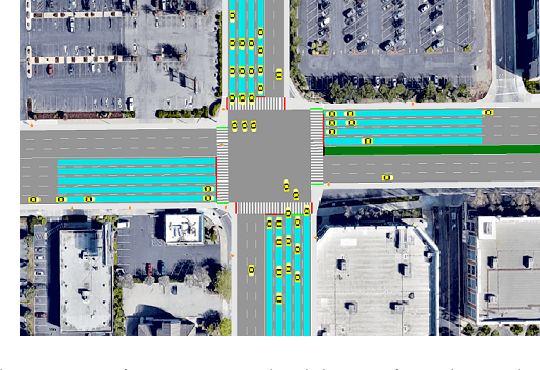
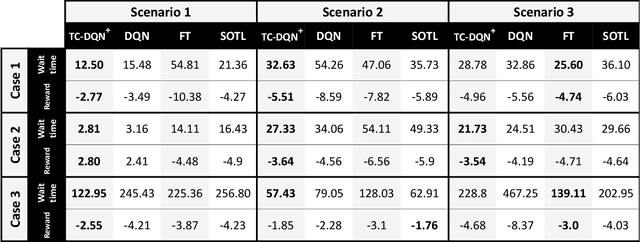
In this work, we study adaptive data-guided traffic planning and control using Reinforcement Learning (RL). We shift from the plain use of classic methods towards state-of-the-art in deep RL community. We embed several recent techniques in our algorithm that improve the original Deep Q-Networks (DQN) for discrete control and discuss the traffic-related interpretations that follow. We propose a novel DQN-based algorithm for Traffic Control (called TC-DQN+) as a tool for fast and more reliable traffic decision-making. We introduce a new form of reward function which is further discussed using illustrative examples with comparisons to traditional traffic control methods.

Deep Learning-based Resource Allocation for Infrastructure Resilience

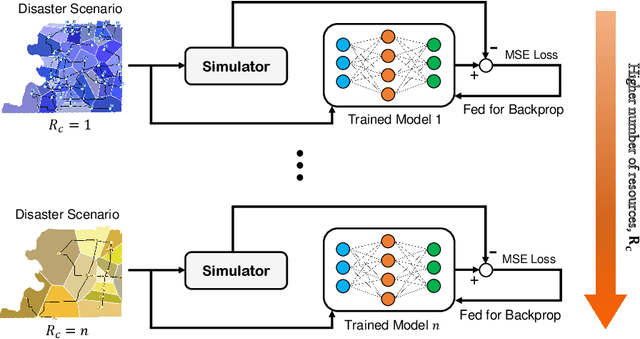
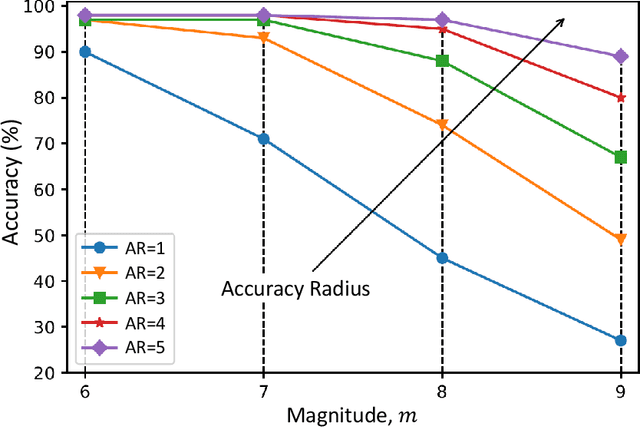
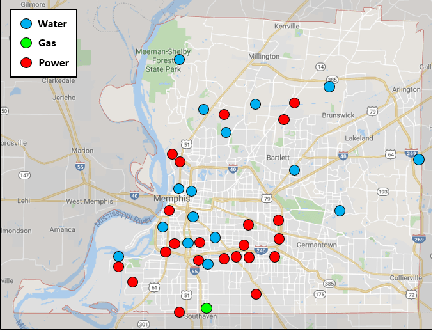
From an optimization point of view, resource allocation is one of the cornerstones of research for addressing limiting factors commonly arising in applications such as power outages and traffic jams. In this paper, we take a data-driven approach to estimate an optimal nodal restoration sequence for immediate recovery of the infrastructure networks after natural disasters such as earthquakes. We generate data from td-INDP, a high-fidelity simulator of optimal restoration strategies for interdependent networks, and employ deep neural networks to approximate those strategies. Despite the fact that the underlying problem is NP-complete, the restoration sequences obtained by our method are observed to be nearly optimal. In addition, by training multiple models---the so-called estimators---for a variety of resource availability levels, our proposed method balances a trade-off between resource utilization and restoration time. Decision-makers can use our trained models to allocate resources more efficiently after contingencies, and in turn, improve the community resilience. Besides their predictive power, such trained estimators unravel the effect of interdependencies among different nodal functionalities in the restoration strategies. We showcase our methodology by the real-world interdependent infrastructure of Shelby County, TN.

Online Regulation of Unstable LTI Systems from a Single Trajectory

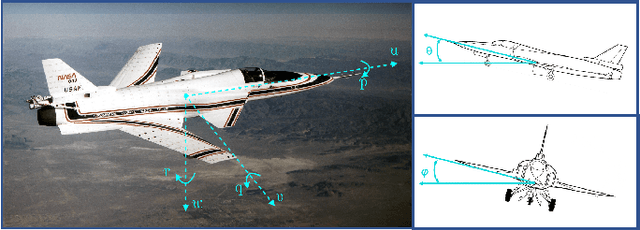
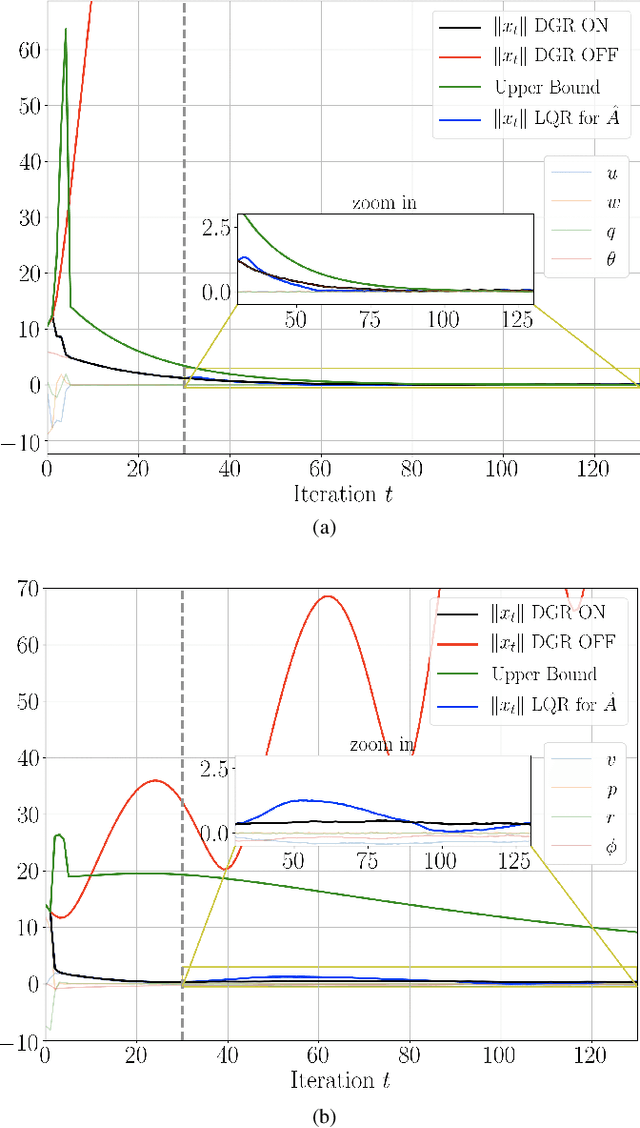
Recently, data-driven methods for control of dynamic systems have received considerable attention in system theory and machine learning as they provide a mechanism for feedback synthesis from the observed time-series data. However learning, say through direct policy updates, often requires assumptions such as knowing a priori that the initial policy (gain) is stabilizing, e.g., when the open-loop system is stable. In this paper, we examine online regulation of (possibly unstable) partially unknown linear systems with no a priori assumptions on the initial controller. First, we introduce and characterize the notion of ''regularizability'' for linear systems that gauges the capacity of a system to be regulated in finite-time in contrast to its asymptotic behavior (commonly characterized by stabilizability/controllability). Next, having access only to the input matrix, we propose the Data-GuidedRegulation (DGR) synthesis that--as its name suggests--regulates the underlying states while also generating informative data that can subsequently be used for data-driven stabilization or system identification (sysID). The analysis is also related in spirit, to thespectrum and the ''instability number'' of the underlying linear system, a novel geometric property studied in this work. We further elucidate our results by considering special structures for system parameters as well as boosting the performance of the algorithm via a rank-one matrix update using the discrete nature of data collection in the problem setup. Finally, we demonstrate the utility of the proposed approach via an example involving direct (online) regulation of the X-29 aircraft.

Global Convergence of Policy Gradient Methods for the Linear Quadratic Regulator

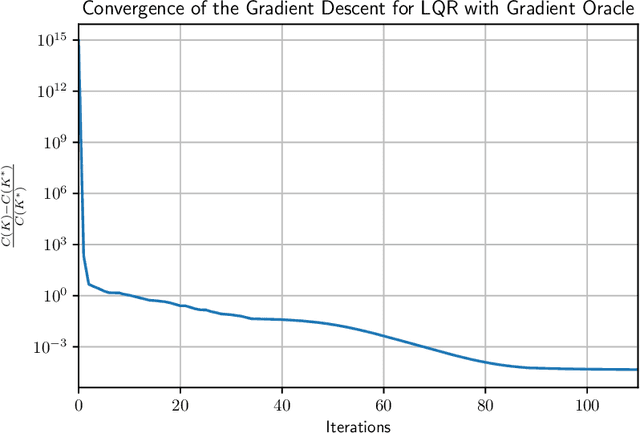
Direct policy gradient methods for reinforcement learning and continuous control problems are a popular approach for a variety of reasons: 1) they are easy to implement without explicit knowledge of the underlying model 2) they are an "end-to-end" approach, directly optimizing the performance metric of interest 3) they inherently allow for richly parameterized policies. A notable drawback is that even in the most basic continuous control problem (that of linear quadratic regulators), these methods must solve a non-convex optimization problem, where little is understood about their efficiency from both computational and statistical perspectives. In contrast, system identification and model based planning in optimal control theory have a much more solid theoretical footing, where much is known with regards to their computational and statistical properties. This work bridges this gap showing that (model free) policy gradient methods globally converge to the optimal solution and are efficient (polynomially so in relevant problem dependent quantities) with regards to their sample and computational complexities.

Online Distributed Optimization on Dynamic Networks

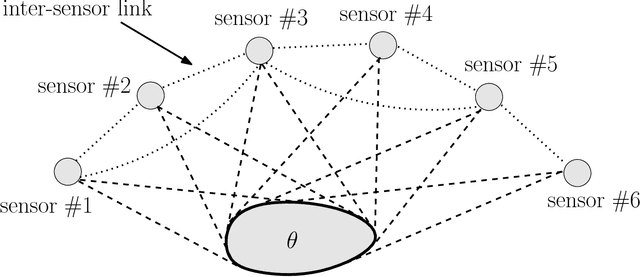
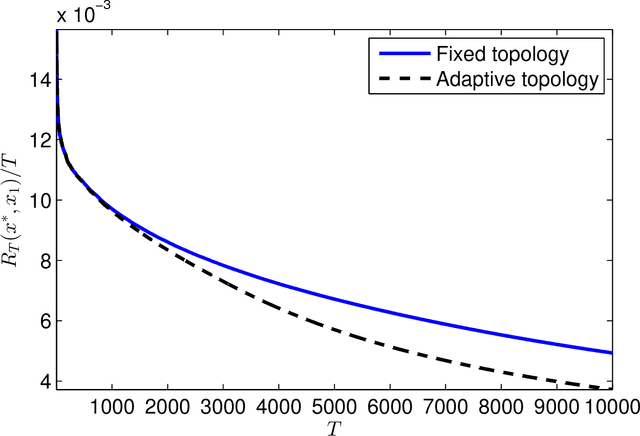
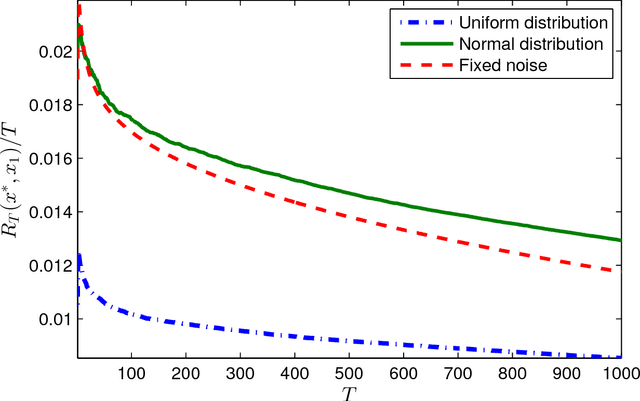
This paper presents a distributed optimization scheme over a network of agents in the presence of cost uncertainties and over switching communication topologies. Inspired by recent advances in distributed convex optimization, we propose a distributed algorithm based on a dual sub-gradient averaging. The objective of this algorithm is to minimize a cost function cooperatively. Furthermore, the algorithm changes the weights on the communication links in the network to adapt to varying reliability of neighboring agents. A convergence rate analysis as a function of the underlying network topology is then presented, followed by simulation results for representative classes of sensor networks.