Learning Low-dimensional Latent Dynamics from High-dimensional Observations: Non-asymptotics and Lower Bounds

In this paper, we focus on learning a linear time-invariant (LTI) model with low-dimensional latent variables but high-dimensional observations. We provide an algorithm that recovers the high-dimensional features, i.e. column space of the observer, embeds the data into low dimensions and learns the low-dimensional model parameters. Our algorithm enjoys a sample complexity guarantee of order $\tilde{\mathcal{O}}(n/\epsilon^2)$, where $n$ is the observation dimension. We further establish a fundamental lower bound indicating this complexity bound is optimal up to logarithmic factors and dimension-independent constants. We show that this inevitable linear factor of $n$ is due to the learning error of the observer's column space in the presence of high-dimensional noise. Extending our results, we consider a meta-learning problem inspired by various real-world applications, where the observer column space can be collectively learned from datasets of multiple LTI systems. An end-to-end algorithm is then proposed, facilitating learning LTI systems from a meta-dataset which breaks the sample complexity lower bound in certain scenarios.

Duality-Based Stochastic Policy Optimization for Estimation with Unknown Noise Covariances

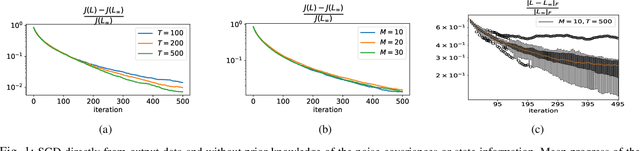
Duality of control and estimation allows mapping recent advances in data-guided control to the estimation setup. This paper formalizes and utilizes such a mapping by considering learning the optimal (steady-state) Kalman gain when process and measurement noise statistics are unknown. Specifically, building on the duality between synthesizing optimal control and estimation gains, the filter design problem is formalized as direct policy learning; subsequently, a Stochastic Gradient Descent (SGD) approach is adopted to learn the optimal filter gain. In this direction, control and estimation duality is also used to extend existing theoretical results for direct policy updates for Linear Quadratic Regulator (LQR) to establish convergence of the proposed algorithm-while addressing subtle differences between the two synthesis problems. The results are illustrated via several numerical examples.

Deep Learning-based Resource Allocation for Infrastructure Resilience

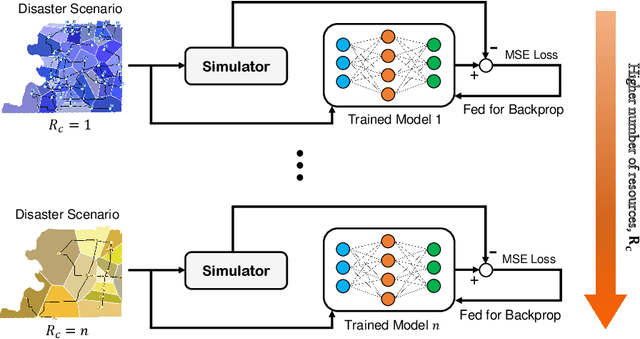
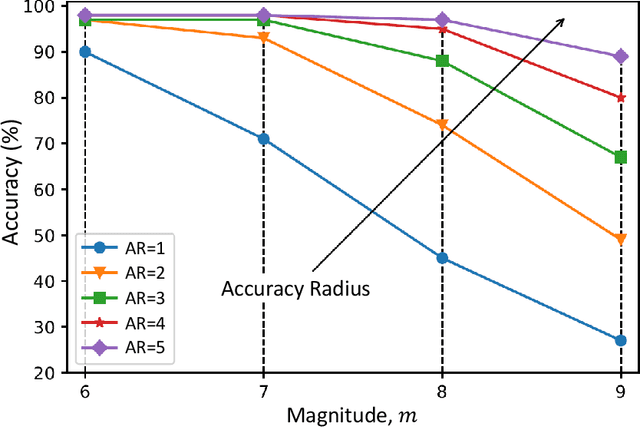
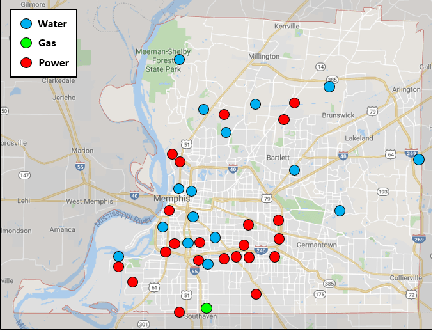
From an optimization point of view, resource allocation is one of the cornerstones of research for addressing limiting factors commonly arising in applications such as power outages and traffic jams. In this paper, we take a data-driven approach to estimate an optimal nodal restoration sequence for immediate recovery of the infrastructure networks after natural disasters such as earthquakes. We generate data from td-INDP, a high-fidelity simulator of optimal restoration strategies for interdependent networks, and employ deep neural networks to approximate those strategies. Despite the fact that the underlying problem is NP-complete, the restoration sequences obtained by our method are observed to be nearly optimal. In addition, by training multiple models---the so-called estimators---for a variety of resource availability levels, our proposed method balances a trade-off between resource utilization and restoration time. Decision-makers can use our trained models to allocate resources more efficiently after contingencies, and in turn, improve the community resilience. Besides their predictive power, such trained estimators unravel the effect of interdependencies among different nodal functionalities in the restoration strategies. We showcase our methodology by the real-world interdependent infrastructure of Shelby County, TN.

Online Regulation of Unstable LTI Systems from a Single Trajectory

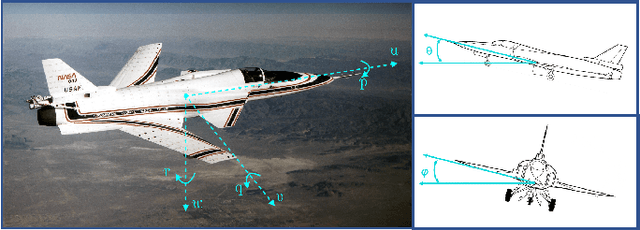
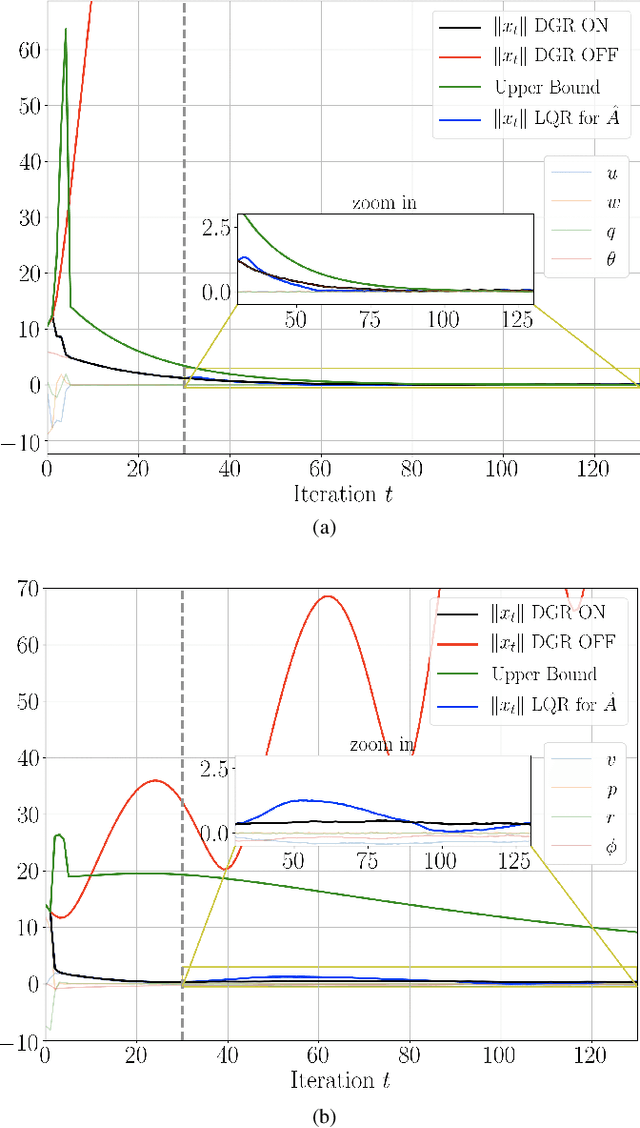
Recently, data-driven methods for control of dynamic systems have received considerable attention in system theory and machine learning as they provide a mechanism for feedback synthesis from the observed time-series data. However learning, say through direct policy updates, often requires assumptions such as knowing a priori that the initial policy (gain) is stabilizing, e.g., when the open-loop system is stable. In this paper, we examine online regulation of (possibly unstable) partially unknown linear systems with no a priori assumptions on the initial controller. First, we introduce and characterize the notion of ''regularizability'' for linear systems that gauges the capacity of a system to be regulated in finite-time in contrast to its asymptotic behavior (commonly characterized by stabilizability/controllability). Next, having access only to the input matrix, we propose the Data-GuidedRegulation (DGR) synthesis that--as its name suggests--regulates the underlying states while also generating informative data that can subsequently be used for data-driven stabilization or system identification (sysID). The analysis is also related in spirit, to thespectrum and the ''instability number'' of the underlying linear system, a novel geometric property studied in this work. We further elucidate our results by considering special structures for system parameters as well as boosting the performance of the algorithm via a rank-one matrix update using the discrete nature of data collection in the problem setup. Finally, we demonstrate the utility of the proposed approach via an example involving direct (online) regulation of the X-29 aircraft.