Niyousha Rahimi
Data-Guided Regulator for Adaptive Nonlinear Control
Nov 20, 2023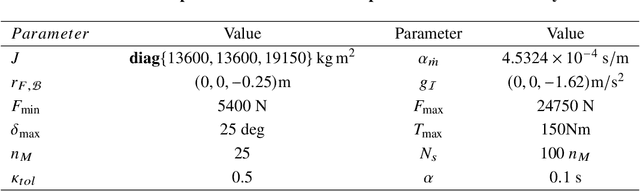
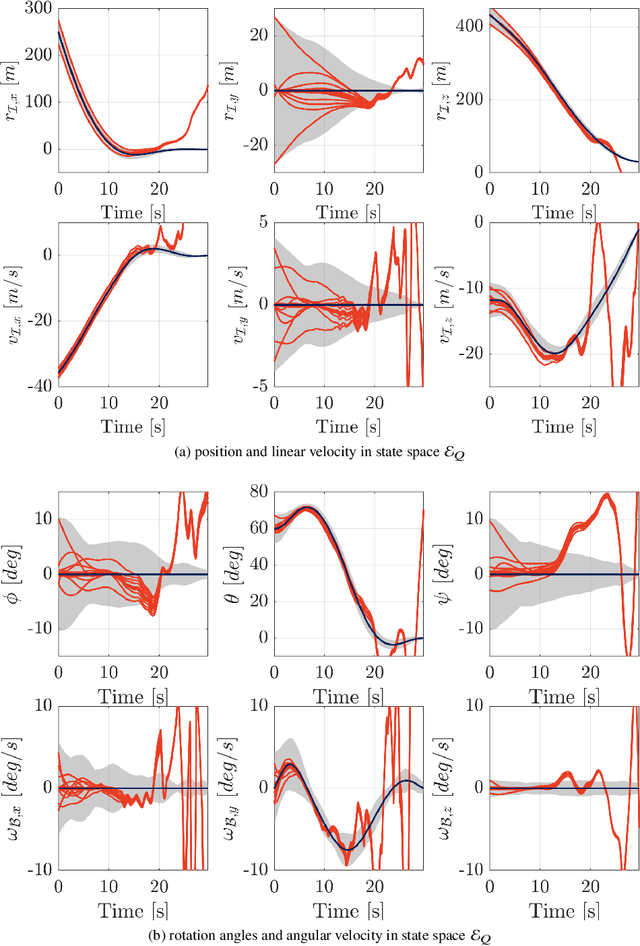
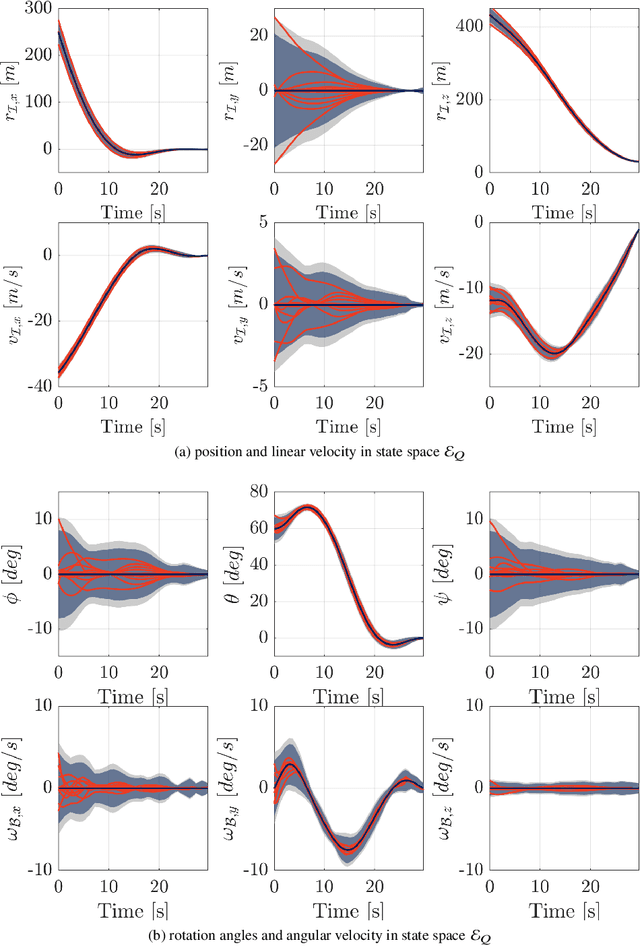
Abstract:This paper addresses the problem of designing a data-driven feedback controller for complex nonlinear dynamical systems in the presence of time-varying disturbances with unknown dynamics. Such disturbances are modeled as the "unknown" part of the system dynamics. The goal is to achieve finite-time regulation of system states through direct policy updates while also generating informative data that can subsequently be used for data-driven stabilization or system identification. First, we expand upon the notion of "regularizability" and characterize this system characteristic for a linear time-varying representation of the nonlinear system with locally-bounded higher-order terms. "Rapid-regularizability" then gauges the extent by which a system can be regulated in finite time, in contrast to its asymptotic behavior. We then propose the Data-Guided Regulation for Adaptive Nonlinear Control ( DG-RAN) algorithm, an online iterative synthesis procedure that utilizes discrete time-series data from a single trajectory for regulating system states and identifying disturbance dynamics. The effectiveness of our approach is demonstrated on a 6-DOF power descent guidance problem in the presence of adverse environmental disturbances.
Online Regulation of Unstable LTI Systems from a Single Trajectory
Jun 09, 2020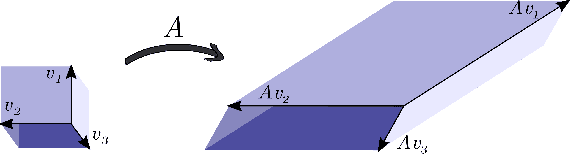
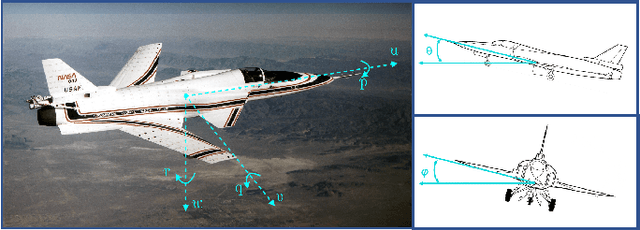
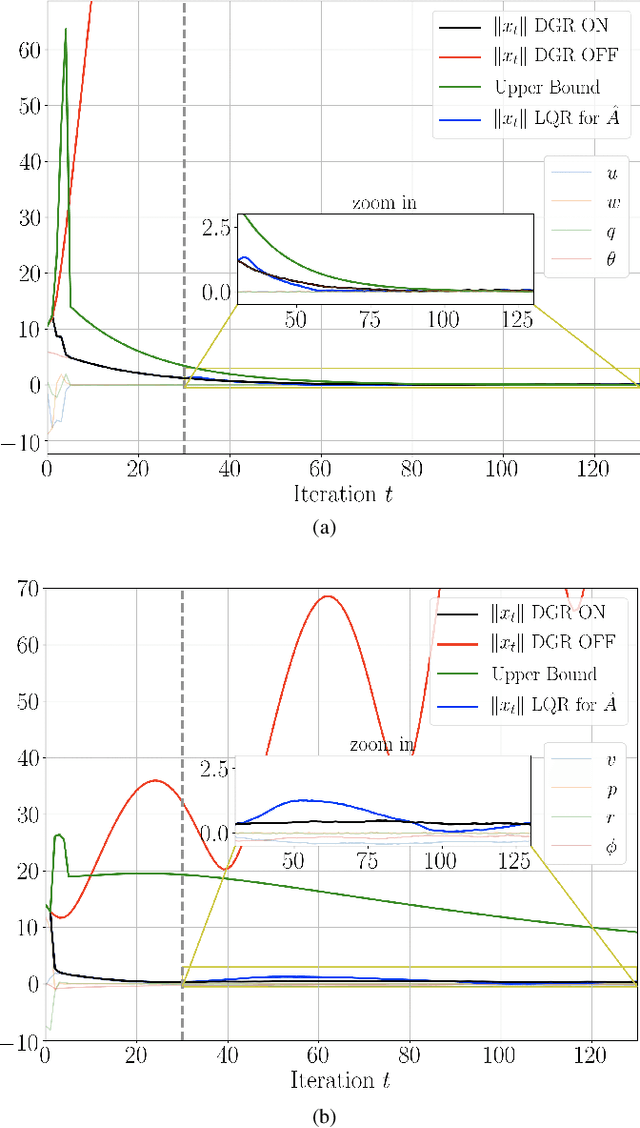
Abstract:Recently, data-driven methods for control of dynamic systems have received considerable attention in system theory and machine learning as they provide a mechanism for feedback synthesis from the observed time-series data. However learning, say through direct policy updates, often requires assumptions such as knowing a priori that the initial policy (gain) is stabilizing, e.g., when the open-loop system is stable. In this paper, we examine online regulation of (possibly unstable) partially unknown linear systems with no a priori assumptions on the initial controller. First, we introduce and characterize the notion of ''regularizability'' for linear systems that gauges the capacity of a system to be regulated in finite-time in contrast to its asymptotic behavior (commonly characterized by stabilizability/controllability). Next, having access only to the input matrix, we propose the Data-GuidedRegulation (DGR) synthesis that--as its name suggests--regulates the underlying states while also generating informative data that can subsequently be used for data-driven stabilization or system identification (sysID). The analysis is also related in spirit, to thespectrum and the ''instability number'' of the underlying linear system, a novel geometric property studied in this work. We further elucidate our results by considering special structures for system parameters as well as boosting the performance of the algorithm via a rank-one matrix update using the discrete nature of data collection in the problem setup. Finally, we demonstrate the utility of the proposed approach via an example involving direct (online) regulation of the X-29 aircraft.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge