Data-Guided Regulator for Adaptive Nonlinear Control
Paper and Code
Nov 20, 2023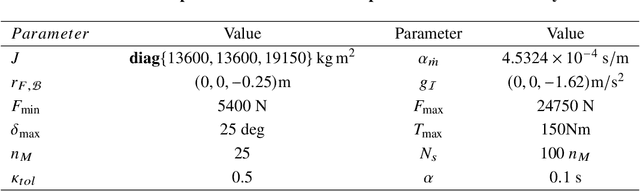
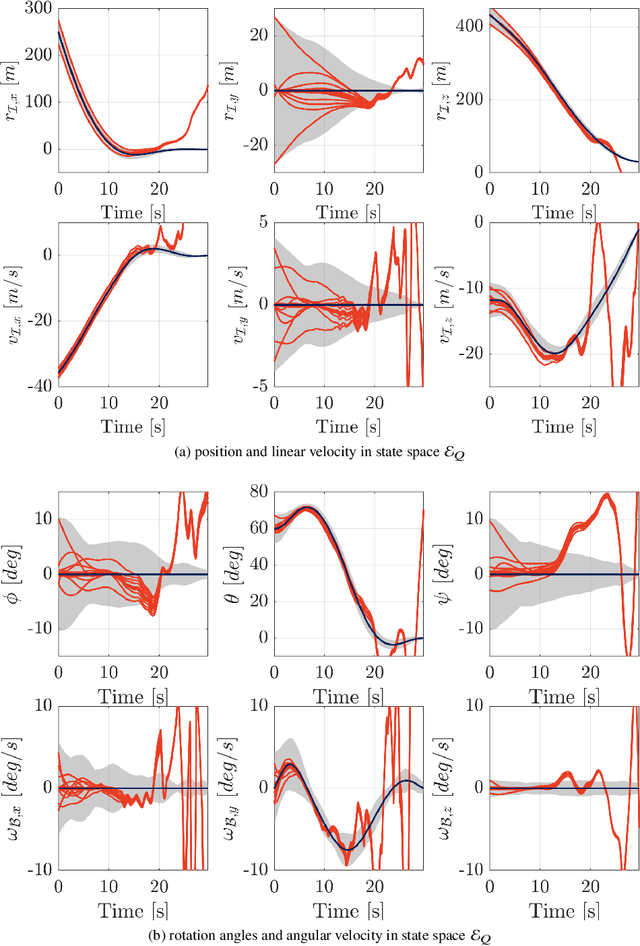
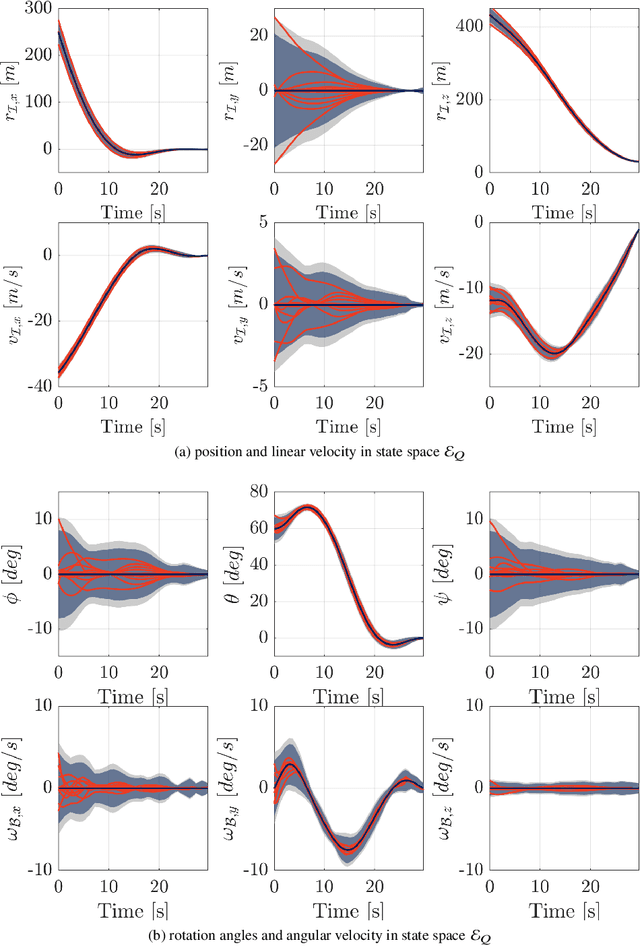
This paper addresses the problem of designing a data-driven feedback controller for complex nonlinear dynamical systems in the presence of time-varying disturbances with unknown dynamics. Such disturbances are modeled as the "unknown" part of the system dynamics. The goal is to achieve finite-time regulation of system states through direct policy updates while also generating informative data that can subsequently be used for data-driven stabilization or system identification. First, we expand upon the notion of "regularizability" and characterize this system characteristic for a linear time-varying representation of the nonlinear system with locally-bounded higher-order terms. "Rapid-regularizability" then gauges the extent by which a system can be regulated in finite time, in contrast to its asymptotic behavior. We then propose the Data-Guided Regulation for Adaptive Nonlinear Control ( DG-RAN) algorithm, an online iterative synthesis procedure that utilizes discrete time-series data from a single trajectory for regulating system states and identifying disturbance dynamics. The effectiveness of our approach is demonstrated on a 6-DOF power descent guidance problem in the presence of adverse environmental disturbances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge