Guided Transfer Learning for Discrete Diffusion Models

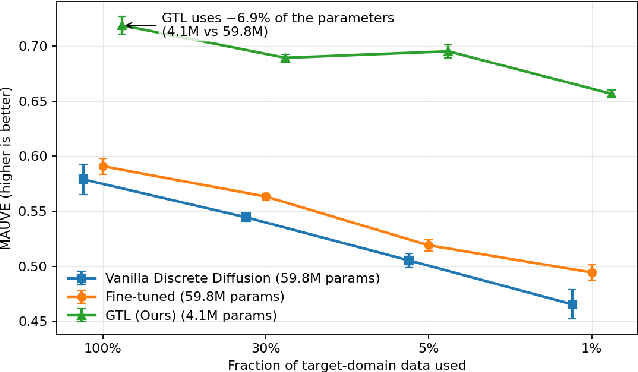
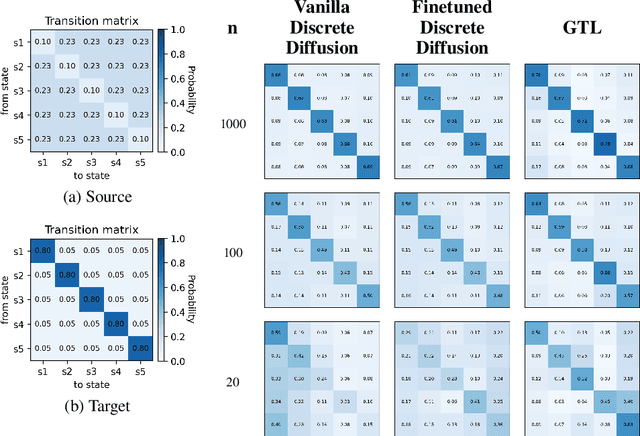
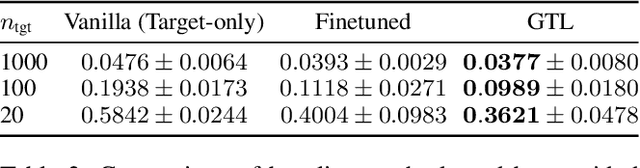
Discrete diffusion models achieve strong performance across language and other discrete domains, providing a powerful alternative to autoregressive models. However, their strong performance relies on large training datasets, which are costly or risky to obtain, especially when adapting to new domains. Transfer learning is the natural way to adapt pretrained discrete diffusion models, but current methods require fine-tuning large diffusion models, which is computationally expensive and often impractical. Building on ratio-based transfer learning for continuous diffusion, we provide Guided Transfer Learning for discrete diffusion models (GTL). This enables sampling from a target distribution without modifying the pretrained denoiser. The same guidance formulation applies to both discrete-time diffusion and continuous-time score-based discrete diffusion, yielding a unified treatment. Guided discrete diffusion often requires many forward passes of the guidance network, which becomes impractical for large vocabularies and long sequences. To address this, we further present an efficient guided sampler that concentrates evaluations on planner-selected positions and top candidate tokens, thus lowering sampling time and computation. This makes guided language modeling practical at scale for large vocabularies and long sequences. We evaluate GTL on sequential data, including synthetic Markov chains and language modeling, and provide empirical analyses of its behavior.

ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

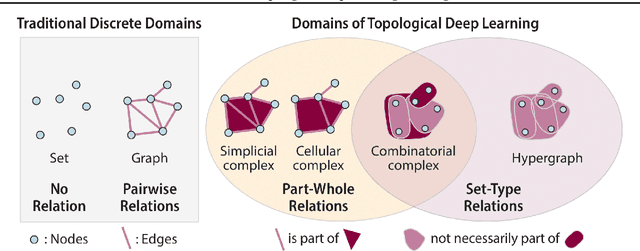
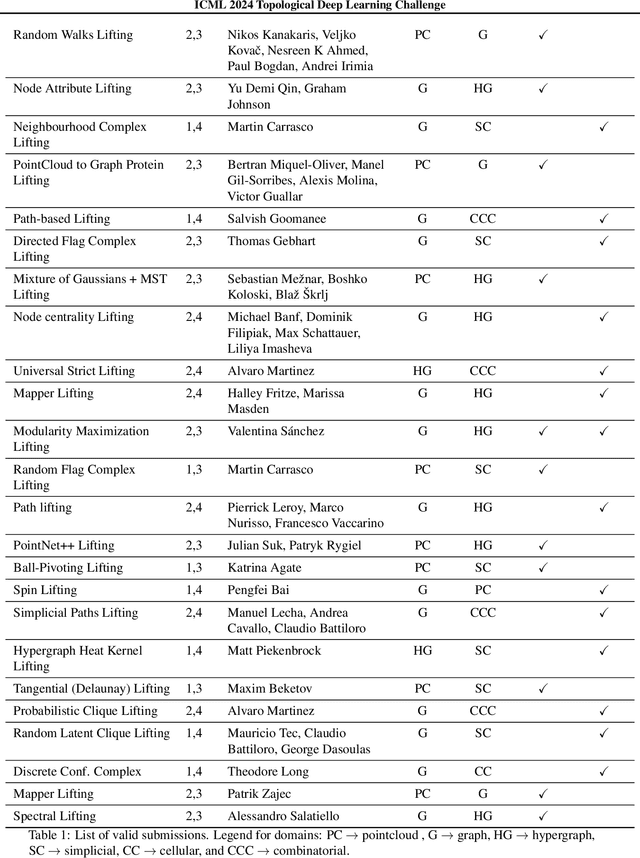
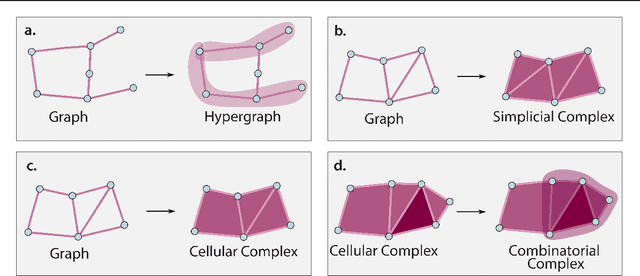
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

E(n) Equivariant Topological Neural Networks

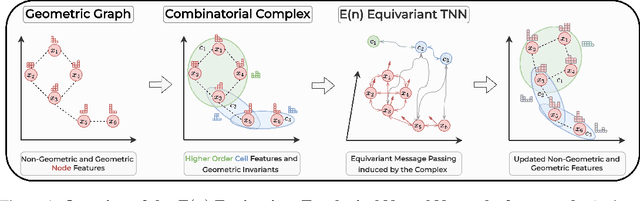
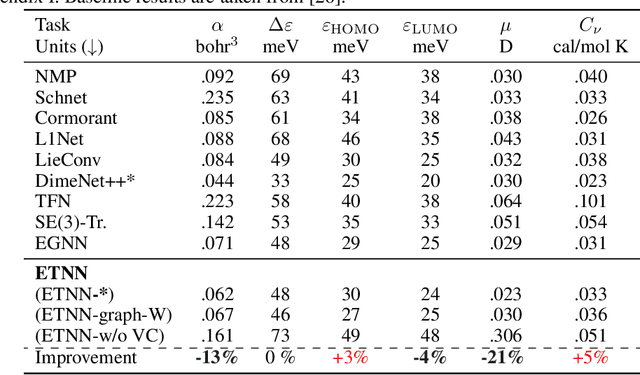
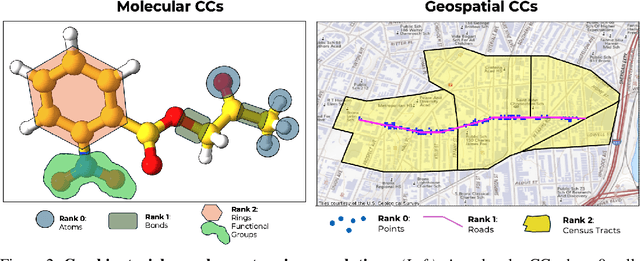
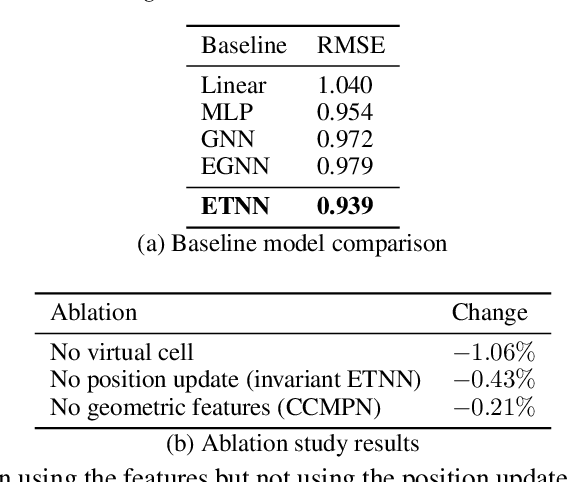
Graph neural networks excel at modeling pairwise interactions, but they cannot flexibly accommodate higher-order interactions and features. Topological deep learning (TDL) has emerged recently as a promising tool for addressing this issue. TDL enables the principled modeling of arbitrary multi-way, hierarchical higher-order interactions by operating on combinatorial topological spaces, such as simplicial or cell complexes, instead of graphs. However, little is known about how to leverage geometric features such as positions and velocities for TDL. This paper introduces E(n)-Equivariant Topological Neural Networks (ETNNs), which are E(n)-equivariant message-passing networks operating on combinatorial complexes, formal objects unifying graphs, hypergraphs, simplicial, path, and cell complexes. ETNNs incorporate geometric node features while respecting rotation and translation equivariance. Moreover, ETNNs are natively ready for settings with heterogeneous interactions. We provide a theoretical analysis to show the improved expressiveness of ETNNs over architectures for geometric graphs. We also show how several E(n) equivariant variants of TDL models can be directly derived from our framework. The broad applicability of ETNNs is demonstrated through two tasks of vastly different nature: i) molecular property prediction on the QM9 benchmark and ii) land-use regression for hyper-local estimation of air pollution with multi-resolution irregular geospatial data. The experiment results indicate that ETNNs are an effective tool for learning from diverse types of richly structured data, highlighting the benefits of principled geometric inductive bias.

Optimizing Heat Alert Issuance for Public Health in the United States with Reinforcement Learning

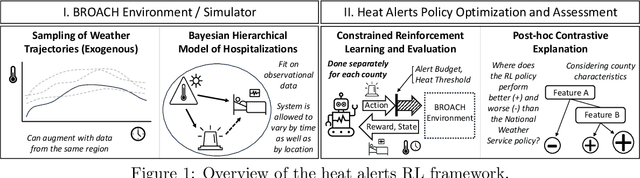
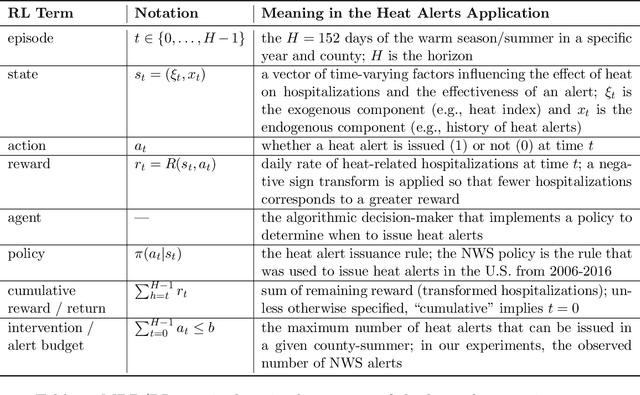
Alerting the public when heat may harm their health is a crucial service, especially considering that extreme heat events will be more frequent under climate change. Current practice for issuing heat alerts in the US does not take advantage of modern data science methods for optimizing local alert criteria. Specifically, application of reinforcement learning (RL) has the potential to inform more health-protective policies, accounting for regional and sociodemographic heterogeneity as well as sequential dependence of alerts. In this work, we formulate the issuance of heat alerts as a sequential decision making problem and develop modifications to the RL workflow to address challenges commonly encountered in environmental health settings. Key modifications include creating a simulator that pairs hierarchical Bayesian modeling of low-signal health effects with sampling of real weather trajectories (exogenous features), constraining the total number of alerts issued as well as preventing alerts on less-hot days, and optimizing location-specific policies. Post-hoc contrastive analysis offers insights into scenarios when using RL for heat alert issuance may protect public health better than the current or alternative policies. This work contributes to a broader movement of advancing data-driven policy optimization for public health and climate change adaptation.

SpaCE: The Spatial Confounding Environment

Spatial confounding poses a significant challenge in scientific studies involving spatial data, where unobserved spatial variables can influence both treatment and outcome, possibly leading to spurious associations. To address this problem, we introduce SpaCE: The Spatial Confounding Environment, the first toolkit to provide realistic benchmark datasets and tools for systematically evaluating causal inference methods designed to alleviate spatial confounding. Each dataset includes training data, true counterfactuals, a spatial graph with coordinates, and smoothness and confounding scores characterizing the effect of a missing spatial confounder. It also includes realistic semi-synthetic outcomes and counterfactuals, generated using state-of-the-art machine learning ensembles, following best practices for causal inference benchmarks. The datasets cover real treatment and covariates from diverse domains, including climate, health and social sciences. SpaCE facilitates an automated end-to-end pipeline, simplifying data loading, experimental setup, and evaluating machine learning and causal inference models. The SpaCE project provides several dozens of datasets of diverse sizes and spatial complexity. It is publicly available as a Python package, encouraging community feedback and contributions.

Causal Shift-Response Functions with Neural Networks: The Health Benefits of Lowering Air Quality Standards in the US

Policymakers are required to evaluate the health benefits of reducing the National Ambient Air Quality Standards (NAAQS; i.e., the safety standards) for fine particulate matter PM 2.5 before implementing new policies. We formulate this objective as a shift-response function (SRF) and develop methods to analyze the problem using methods for causal inference, specifically under the stochastic interventions framework. SRFs model the average change in an outcome of interest resulting from a hypothetical shift in the observed exposure distribution. We propose a new broadly applicable doubly-robust method to learn SRFs using targeted regularization with neural networks. We evaluate our proposed method under various benchmarks specific for marginal estimates as a function of continuous exposure. Finally, we implement our estimator in the motivating application that considers the potential reduction in deaths from lowering the NAAQS from the current level of 12 $\mu g/m^3$ to levels that are recently proposed by the Environmental Protection Agency in the US (10, 9, and 8 $\mu g/m^3$).

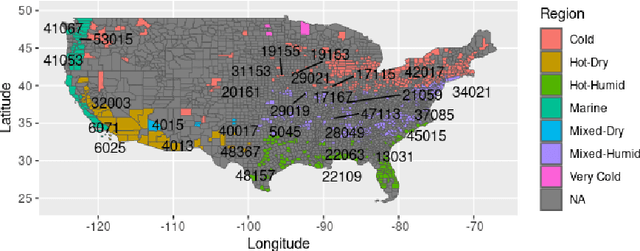
Weather2vec: Representation Learning for Causal Inference with Non-Local Confounding in Air Pollution and Climate Studies

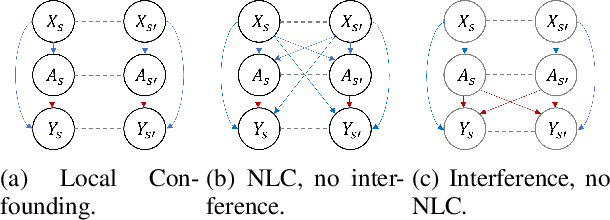
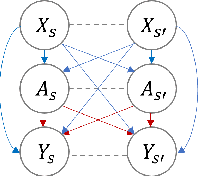
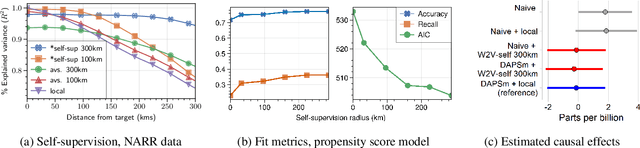
Estimating the causal effects of a spatially-varying intervention on a spatially-varying outcome may be subject to non-local confounding (NLC), a phenomenon that can bias estimates when the treatments and outcomes of a given unit are dictated in part by the covariates of other nearby units. In particular, NLC is a challenge for evaluating the effects of environmental policies and climate events on health-related outcomes such as air pollution exposure. This paper first formalizes NLC using the potential outcomes framework, providing a comparison with the related phenomenon of causal interference. Then, it proposes a broadly applicable framework, termed "weather2vec", that uses the theory of balancing scores to learn representations of non-local information into a scalar or vector defined for each observational unit, which is subsequently used to adjust for confounding in conjunction with causal inference methods. The framework is evaluated in a simulation study and two case studies on air pollution where the weather is an (inherently regional) known confounder.

Adversarial Intrinsic Motivation for Reinforcement Learning

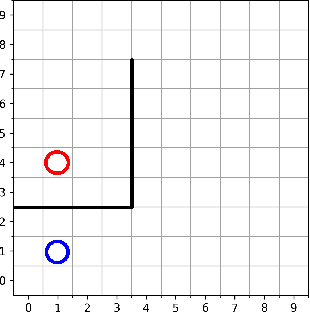
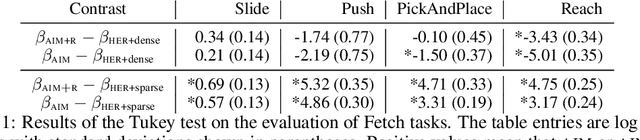
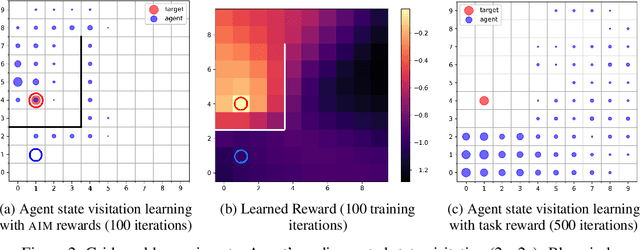
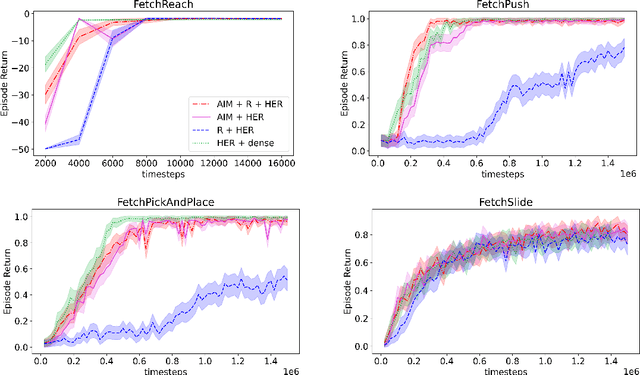
Learning with an objective to minimize the mismatch with a reference distribution has been shown to be useful for generative modeling and imitation learning. In this paper, we investigate whether one such objective, the Wasserstein-1 distance between a policy's state visitation distribution and a target distribution, can be utilized effectively for reinforcement learning (RL) tasks. Specifically, this paper focuses on goal-conditioned reinforcement learning where the idealized (unachievable) target distribution has full measure at the goal. We introduce a quasimetric specific to Markov Decision Processes (MDPs), and show that the policy that minimizes the Wasserstein-1 distance of its state visitation distribution to this target distribution under this quasimetric is the policy that reaches the goal in as few steps as possible. Our approach, termed Adversarial Intrinsic Motivation (AIM), estimates this Wasserstein-1 distance through its dual objective and uses it to compute a supplemental reward function. Our experiments show that this reward function changes smoothly with respect to transitions in the MDP and assists the agent in learning. Additionally, we combine AIM with Hindsight Experience Replay (HER) and show that the resulting algorithm accelerates learning significantly on several simulated robotics tasks when compared to HER with a sparse positive reward at the goal state.