Adversarial Intrinsic Motivation for Reinforcement Learning

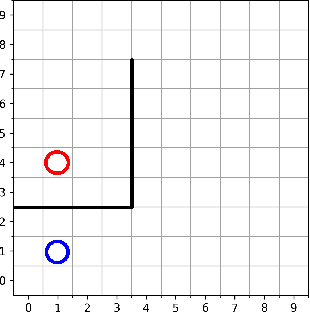
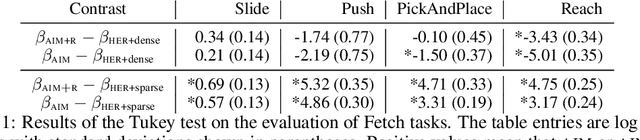
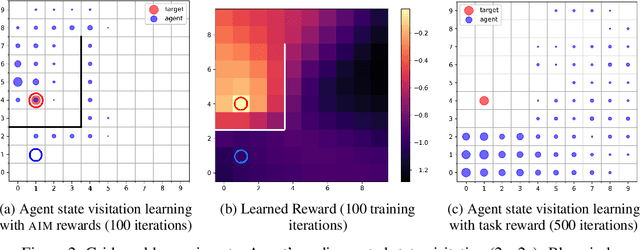
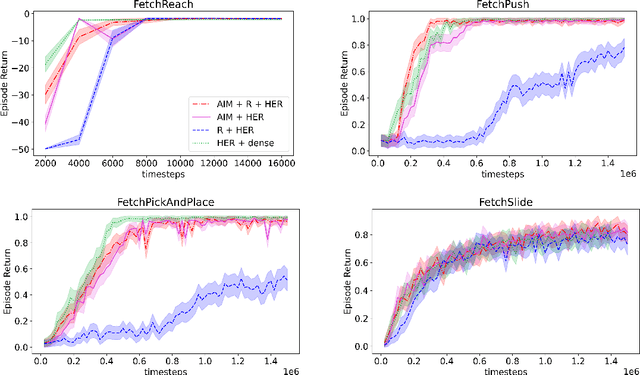
Learning with an objective to minimize the mismatch with a reference distribution has been shown to be useful for generative modeling and imitation learning. In this paper, we investigate whether one such objective, the Wasserstein-1 distance between a policy's state visitation distribution and a target distribution, can be utilized effectively for reinforcement learning (RL) tasks. Specifically, this paper focuses on goal-conditioned reinforcement learning where the idealized (unachievable) target distribution has full measure at the goal. We introduce a quasimetric specific to Markov Decision Processes (MDPs), and show that the policy that minimizes the Wasserstein-1 distance of its state visitation distribution to this target distribution under this quasimetric is the policy that reaches the goal in as few steps as possible. Our approach, termed Adversarial Intrinsic Motivation (AIM), estimates this Wasserstein-1 distance through its dual objective and uses it to compute a supplemental reward function. Our experiments show that this reward function changes smoothly with respect to transitions in the MDP and assists the agent in learning. Additionally, we combine AIM with Hindsight Experience Replay (HER) and show that the resulting algorithm accelerates learning significantly on several simulated robotics tasks when compared to HER with a sparse positive reward at the goal state.