Mauricio Araya-Polo
Uncertainty Quantification in Seismic Inversion Through Integrated Importance Sampling and Ensemble Methods
Sep 10, 2024Abstract:Seismic inversion is essential for geophysical exploration and geological assessment, but it is inherently subject to significant uncertainty. This uncertainty stems primarily from the limited information provided by observed seismic data, which is largely a result of constraints in data collection geometry. As a result, multiple plausible velocity models can often explain the same set of seismic observations. In deep learning-based seismic inversion, uncertainty arises from various sources, including data noise, neural network design and training, and inherent data limitations. This study introduces a novel approach to uncertainty quantification in seismic inversion by integrating ensemble methods with importance sampling. By leveraging ensemble approach in combination with importance sampling, we enhance the accuracy of uncertainty analysis while maintaining computational efficiency. The method involves initializing each model in the ensemble with different weights, introducing diversity in predictions and thereby improving the robustness and reliability of the inversion outcomes. Additionally, the use of importance sampling weights the contribution of each ensemble sample, allowing us to use a limited number of ensemble samples to obtain more accurate estimates of the posterior distribution. Our approach enables more precise quantification of uncertainty in velocity models derived from seismic data. By utilizing a limited number of ensemble samples, this method achieves an accurate and reliable assessment of uncertainty, ultimately providing greater confidence in seismic inversion results.
Distributed Reinforcement Learning for Molecular Design: Antioxidant case
Dec 03, 2023Abstract:Deep reinforcement learning has successfully been applied for molecular discovery as shown by the Molecule Deep Q-network (MolDQN) algorithm. This algorithm has challenges when applied to optimizing new molecules: training such a model is limited in terms of scalability to larger datasets and the trained model cannot be generalized to different molecules in the same dataset. In this paper, a distributed reinforcement learning algorithm for antioxidants, called DA-MolDQN is proposed to address these problems. State-of-the-art bond dissociation energy (BDE) and ionization potential (IP) predictors are integrated into DA-MolDQN, which are critical chemical properties while optimizing antioxidants. Training time is reduced by algorithmic improvements for molecular modifications. The algorithm is distributed, scalable for up to 512 molecules, and generalizes the model to a diverse set of molecules. The proposed models are trained with a proprietary antioxidant dataset. The results have been reproduced with both proprietary and public datasets. The proposed molecules have been validated with DFT simulations and a subset of them confirmed in public "unseen" datasets. In summary, DA-MolDQN is up to 100x faster than previous algorithms and can discover new optimized molecules from proprietary and public antioxidants.
STRIDE: Structure-guided Generation for Inverse Design of Molecules
Nov 06, 2023Abstract:Machine learning and especially deep learning has had an increasing impact on molecule and materials design. In particular, given the growing access to an abundance of high-quality small molecule data for generative modeling for drug design, results for drug discovery have been promising. However, for many important classes of materials such as catalysts, antioxidants, and metal-organic frameworks, such large datasets are not available. Such families of molecules with limited samples and structural similarities are especially prevalent for industrial applications. As is well-known, retraining and even fine-tuning are challenging on such small datasets. Novel, practically applicable molecules are most often derivatives of well-known molecules, suggesting approaches to addressing data scarcity. To address this problem, we introduce $\textbf{STRIDE}$, a generative molecule workflow that generates novel molecules with an unconditional generative model guided by known molecules without any retraining. We generate molecules outside of the training data from a highly specialized set of antioxidant molecules. Our generated molecules have on average 21.7% lower synthetic accessibility scores and also reduce ionization potential by 5.9% of generated molecules via guiding.
Deep Compressed Learning for 3D Seismic Inversion
Oct 31, 2023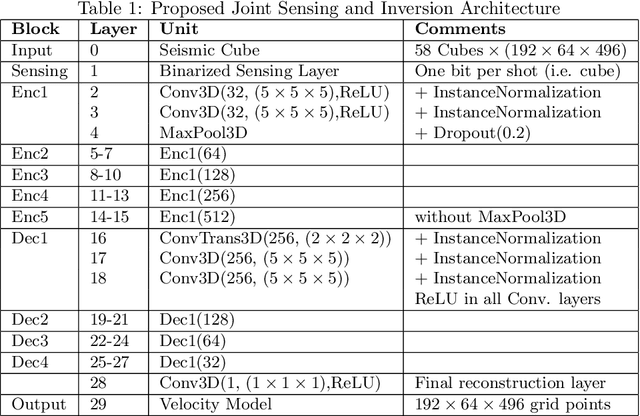
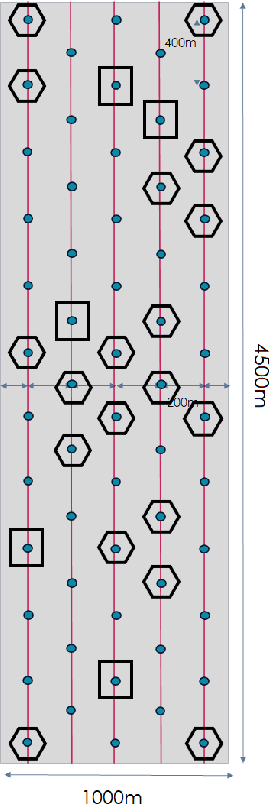
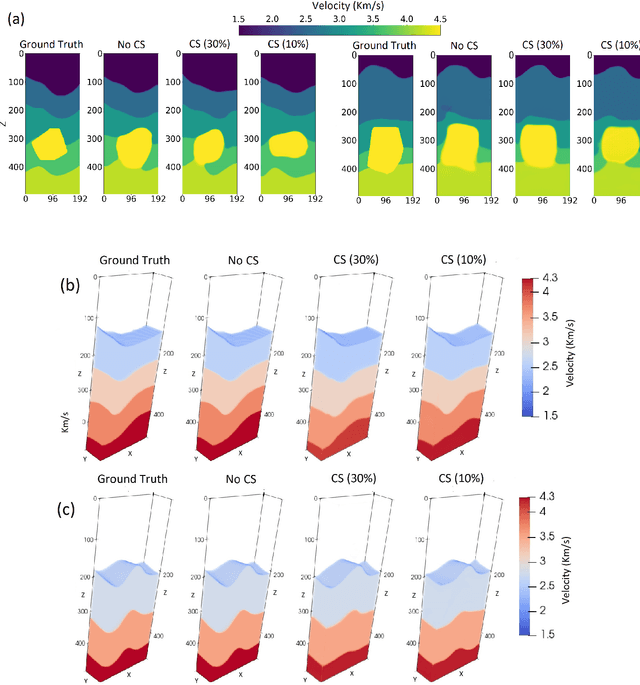
Abstract:We consider the problem of 3D seismic inversion from pre-stack data using a very small number of seismic sources. The proposed solution is based on a combination of compressed-sensing and machine learning frameworks, known as compressed-learning. The solution jointly optimizes a dimensionality reduction operator and a 3D inversion encoder-decoder implemented by a deep convolutional neural network (DCNN). Dimensionality reduction is achieved by learning a sparse binary sensing layer that selects a small subset of the available sources, then the selected data is fed to a DCNN to complete the regression task. The end-to-end learning process provides a reduction by an order-of-magnitude in the number of seismic records used during training, while preserving the 3D reconstruction quality comparable to that obtained by using the entire dataset.
Learning CO$_2$ plume migration in faulted reservoirs with Graph Neural Networks
Jun 16, 2023



Abstract:Deep-learning-based surrogate models provide an efficient complement to numerical simulations for subsurface flow problems such as CO$_2$ geological storage. Accurately capturing the impact of faults on CO$_2$ plume migration remains a challenge for many existing deep learning surrogate models based on Convolutional Neural Networks (CNNs) or Neural Operators. We address this challenge with a graph-based neural model leveraging recent developments in the field of Graph Neural Networks (GNNs). Our model combines graph-based convolution Long-Short-Term-Memory (GConvLSTM) with a one-step GNN model, MeshGraphNet (MGN), to operate on complex unstructured meshes and limit temporal error accumulation. We demonstrate that our approach can accurately predict the temporal evolution of gas saturation and pore pressure in a synthetic reservoir with impermeable faults. Our results exhibit a better accuracy and a reduced temporal error accumulation compared to the standard MGN model. We also show the excellent generalizability of our algorithm to mesh configurations, boundary conditions, and heterogeneous permeability fields not included in the training set. This work highlights the potential of GNN-based methods to accurately and rapidly model subsurface flow with complex faults and fractures.
ParticleGrid: Enabling Deep Learning using 3D Representation of Materials
Nov 15, 2022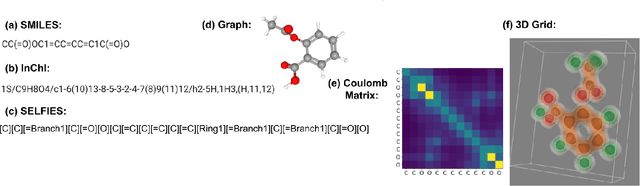
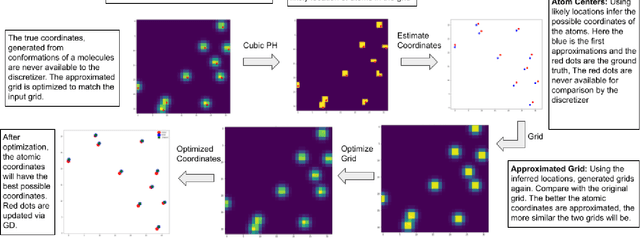
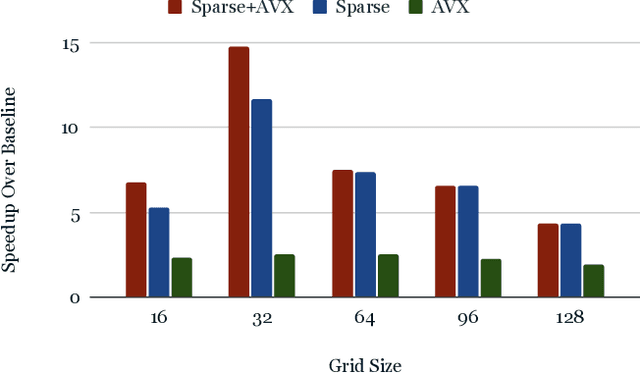
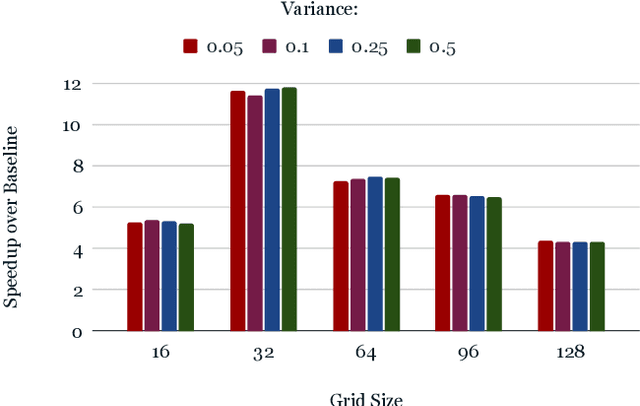
Abstract:From AlexNet to Inception, autoencoders to diffusion models, the development of novel and powerful deep learning models and learning algorithms has proceeded at breakneck speeds. In part, we believe that rapid iteration of model architecture and learning techniques by a large community of researchers over a common representation of the underlying entities has resulted in transferable deep learning knowledge. As a result, model scale, accuracy, fidelity, and compute performance have dramatically increased in computer vision and natural language processing. On the other hand, the lack of a common representation for chemical structure has hampered similar progress. To enable transferable deep learning, we identify the need for a robust 3-dimensional representation of materials such as molecules and crystals. The goal is to enable both materials property prediction and materials generation with 3D structures. While computationally costly, such representations can model a large set of chemical structures. We propose $\textit{ParticleGrid}$, a SIMD-optimized library for 3D structures, that is designed for deep learning applications and to seamlessly integrate with deep learning frameworks. Our highly optimized grid generation allows for generating grids on the fly on the CPU, reducing storage and GPU compute and memory requirements. We show the efficacy of 3D grids generated via $\textit{ParticleGrid}$ and accurately predict molecular energy properties using a 3D convolutional neural network. Our model is able to get 0.006 mean square error and nearly match the values calculated using computationally costly density functional theory at a fraction of the time.
Inversion of Time-Lapse Surface Gravity Data for Detection of 3D CO$_2$ Plumes via Deep Learning
Sep 06, 2022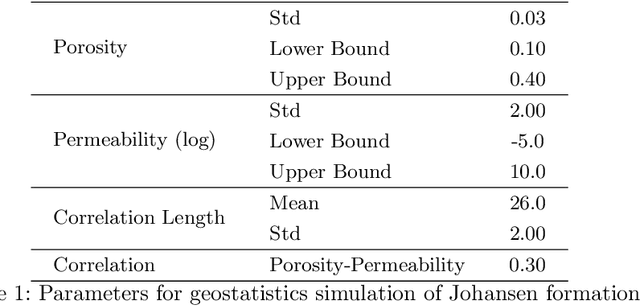
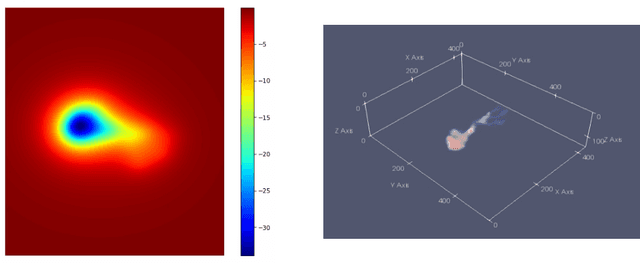
Abstract:We introduce three algorithms that invert simulated gravity data to 3D subsurface rock/flow properties. The first algorithm is a data-driven, deep learning-based approach, the second mixes a deep learning approach with physical modeling into a single workflow, and the third considers the time dependence of surface gravity monitoring. The target application of these proposed algorithms is the prediction of subsurface CO$_2$ plumes as a complementary tool for monitoring CO$_2$ sequestration deployments. Each proposed algorithm outperforms traditional inversion methods and produces high-resolution, 3D subsurface reconstructions in near real-time. Our proposed methods achieve Dice scores of up to 0.8 for predicted plume geometry and near perfect data misfit in terms of $\mu$Gals. These results indicate that combining 4D surface gravity monitoring with deep learning techniques represents a low-cost, rapid, and non-intrusive method for monitoring CO$_2$ storage sites.
Encoder-Decoder Architecture for 3D Seismic Inversion
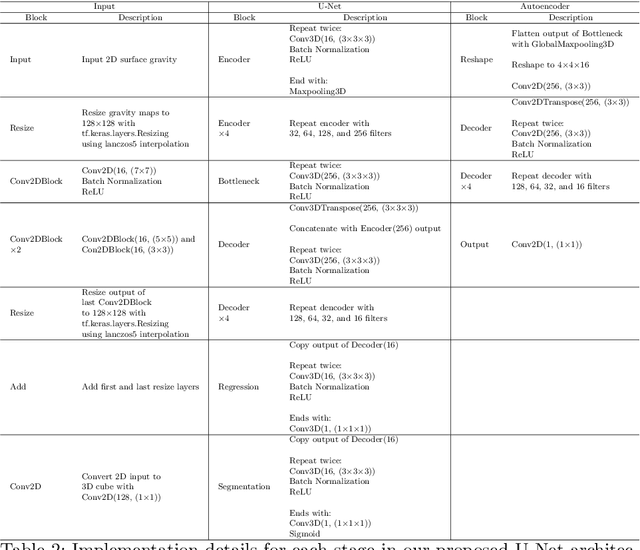
Jul 29, 2022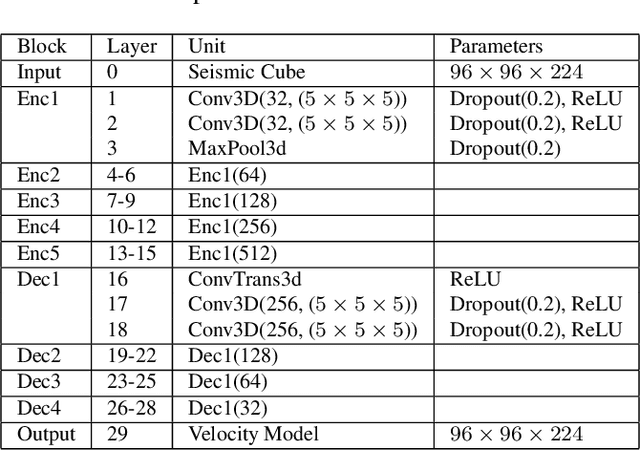
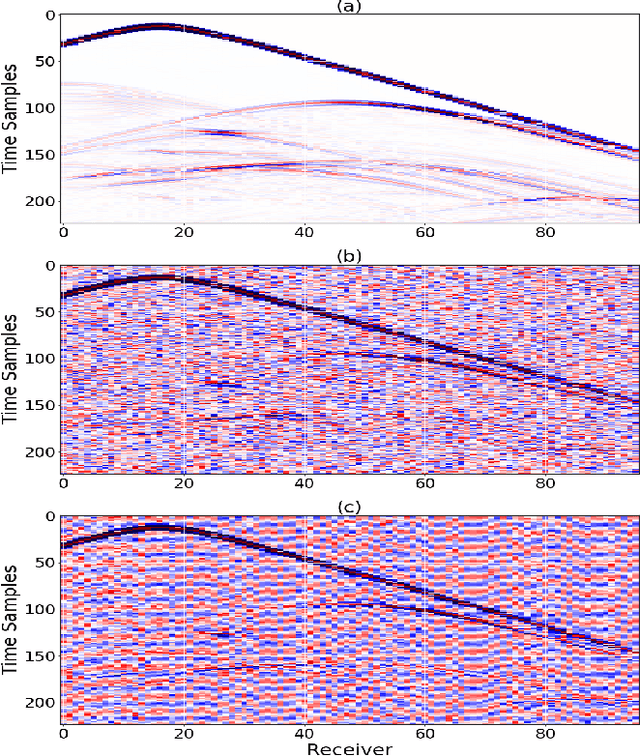

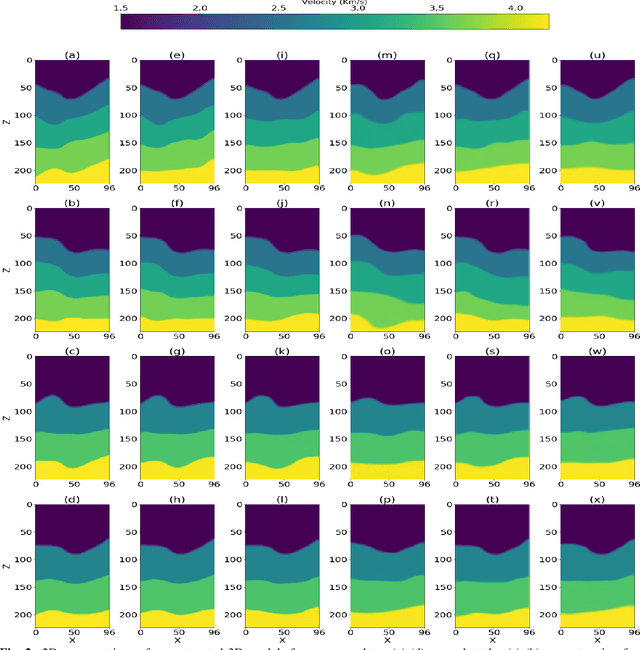
Abstract:Inverting seismic data to build 3D geological structures is a challenging task due to the overwhelming amount of acquired seismic data, and the very-high computational load due to iterative numerical solutions of the wave equation, as required by industry-standard tools such as Full Waveform Inversion (FWI). For example, in an area with surface dimensions of 4.5km $\times$ 4.5km, hundreds of seismic shot-gather cubes are required for 3D model reconstruction, leading to Terabytes of recorded data. This paper presents a deep learning solution for the reconstruction of realistic 3D models in the presence of field noise recorded in seismic surveys. We implement and analyze a convolutional encoder-decoder architecture that efficiently processes the entire collection of hundreds of seismic shot-gather cubes. The proposed solution demonstrates that realistic 3D models can be reconstructed with a structural similarity index measure (SSIM) of 0.8554 (out of 1.0) in the presence of field noise at 10dB signal-to-noise ratio.
Deep Neural Network Learning with Second-Order Optimizers -- a Practical Study with a Stochastic Quasi-Gauss-Newton Method
Apr 06, 2020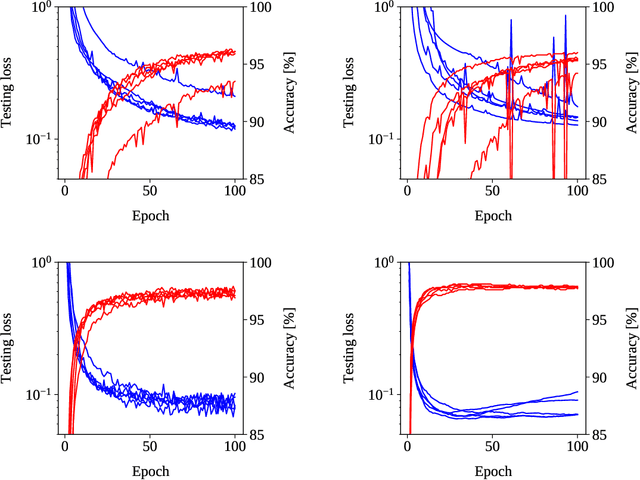

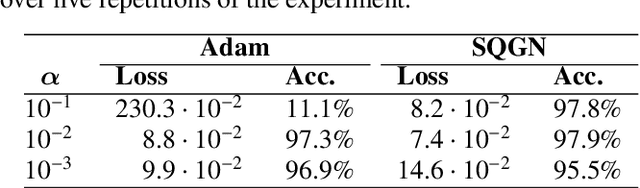
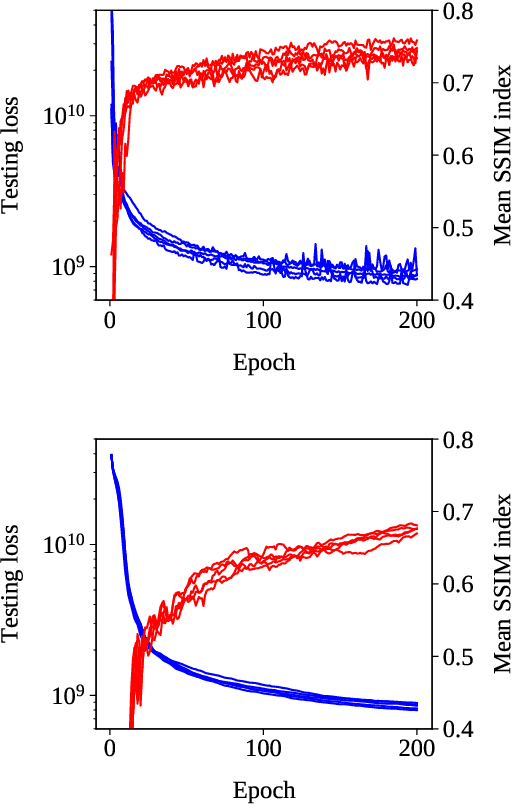
Abstract:Training in supervised deep learning is computationally demanding, and the convergence behavior is usually not fully understood. We introduce and study a second-order stochastic quasi-Gauss--Newton (SQGN) optimization method that combines ideas from stochastic quasi-Newton methods, Gauss--Newton methods, and variance reduction to address this problem. SQGN provides excellent accuracy without the need for experimenting with many hyper-parameter configurations, which is often computationally prohibitive given the number of combinations and the cost of each training process. We discuss the implementation of SQGN with TensorFlow, and we compare its convergence and computational performance to selected first-order methods using the MNIST benchmark and a large-scale seismic tomography application from Earth science.
Learning with a Wasserstein Loss
Dec 30, 2015

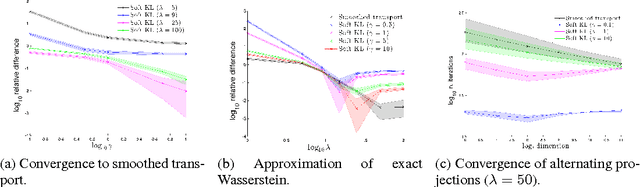
Abstract:Learning to predict multi-label outputs is challenging, but in many problems there is a natural metric on the outputs that can be used to improve predictions. In this paper we develop a loss function for multi-label learning, based on the Wasserstein distance. The Wasserstein distance provides a natural notion of dissimilarity for probability measures. Although optimizing with respect to the exact Wasserstein distance is costly, recent work has described a regularized approximation that is efficiently computed. We describe an efficient learning algorithm based on this regularization, as well as a novel extension of the Wasserstein distance from probability measures to unnormalized measures. We also describe a statistical learning bound for the loss. The Wasserstein loss can encourage smoothness of the predictions with respect to a chosen metric on the output space. We demonstrate this property on a real-data tag prediction problem, using the Yahoo Flickr Creative Commons dataset, outperforming a baseline that doesn't use the metric.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge