Predicting NOx emissions in Biochar Production Plants using Machine Learning

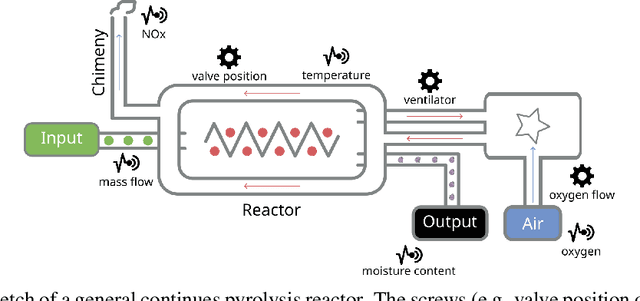
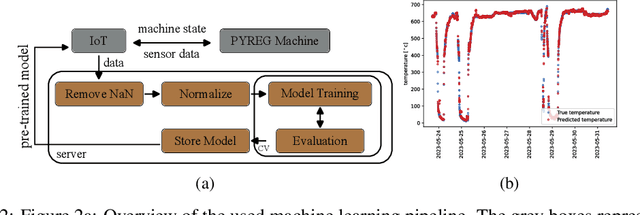
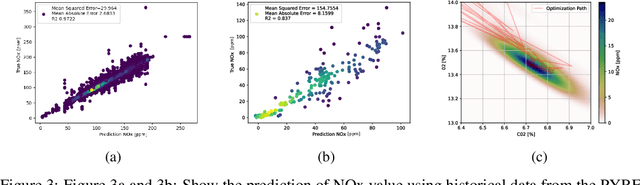
The global Biochar Industry has witnessed a surge in biochar production, with a total of 350k mt/year production in 2023. With the pressing climate goals set and the potential of Biochar Carbon Removal (BCR) as a climate-relevant technology, scaling up the number of new plants to over 1000 facilities per year by 2030 becomes imperative. However, such a massive scale-up presents not only technical challenges but also control and regulation issues, ensuring maximal output of plants while conforming to regulatory requirements. In this paper, we present a novel method of optimizing the process of a biochar plant based on machine learning methods. We show how a standard Random Forest Regressor can be used to model the states of the pyrolysis machine, the physics of which remains highly complex. This model then serves as a surrogate of the machine -- reproducing several key outcomes of the machine -- in a numerical optimization. This, in turn, could enable us to reduce NOx emissions -- a key regulatory goal in that industry -- while achieving maximal output still. In a preliminary test our approach shows remarkable results, proves to be applicable on two different machines from different manufacturers, and can be implemented on standard Internet of Things (IoT) devices more generally.

10 Years of Fair Representations: Challenges and Opportunities

Fair Representation Learning (FRL) is a broad set of techniques, mostly based on neural networks, that seeks to learn new representations of data in which sensitive or undesired information has been removed. Methodologically, FRL was pioneered by Richard Zemel et al. about ten years ago. The basic concepts, objectives and evaluation strategies for FRL methodologies remain unchanged to this day. In this paper, we look back at the first ten years of FRL by i) revisiting its theoretical standing in light of recent work in deep learning theory that shows the hardness of removing information in neural network representations and ii) presenting the results of a massive experimentation (225.000 model fits and 110.000 AutoML fits) we conducted with the objective of improving on the common evaluation scenario for FRL. More specifically, we use automated machine learning (AutoML) to adversarially "mine" sensitive information from supposedly fair representations. Our theoretical and experimental analysis suggests that deterministic, unquantized FRL methodologies have serious issues in removing sensitive information, which is especially troubling as they might seem "fair" at first glance.

Peer Learning: Learning Complex Policies in Groups from Scratch via Action Recommendations

Peer learning is a novel high-level reinforcement learning framework for agents learning in groups. While standard reinforcement learning trains an individual agent in trial-and-error fashion, all on its own, peer learning addresses a related setting in which a group of agents, i.e., peers, learns to master a task simultaneously together from scratch. Peers are allowed to communicate only about their own states and actions recommended by others: "What would you do in my situation?". Our motivation is to study the learning behavior of these agents. We formalize the teacher selection process in the action advice setting as a multi-armed bandit problem and therefore highlight the need for exploration. Eventually, we analyze the learning behavior of the peers and observe their ability to rank the agents' performance within the study group and understand which agents give reliable advice. Further, we compare peer learning with single agent learning and a state-of-the-art action advice baseline. We show that peer learning is able to outperform single-agent learning and the baseline in several challenging discrete and continuous OpenAI Gym domains. Doing so, we also show that within such a framework complex policies from action recommendations beyond discrete action spaces can evolve.

Automated Scientific Discovery: From Equation Discovery to Autonomous Discovery Systems

The paper surveys automated scientific discovery, from equation discovery and symbolic regression to autonomous discovery systems and agents. It discusses the individual approaches from a "big picture" perspective and in context, but also discusses open issues and recent topics like the various roles of deep neural networks in this area, aiding in the discovery of human-interpretable knowledge. Further, we will present closed-loop scientific discovery systems, starting with the pioneering work on the Adam system up to current efforts in fields from material science to astronomy. Finally, we will elaborate on autonomy from a machine learning perspective, but also in analogy to the autonomy levels in autonomous driving. The maximal level, level five, is defined to require no human intervention at all in the production of scientific knowledge. Achieving this is one step towards solving the Nobel Turing Grand Challenge to develop AI Scientists: AI systems capable of making Nobel-quality scientific discoveries highly autonomously at a level comparable, and possibly superior, to the best human scientists by 2050.

Invariant Representations with Stochastically Quantized Neural Networks

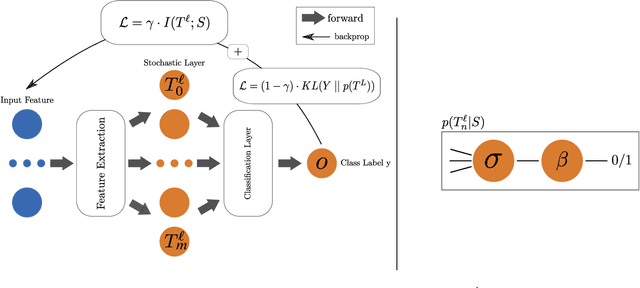
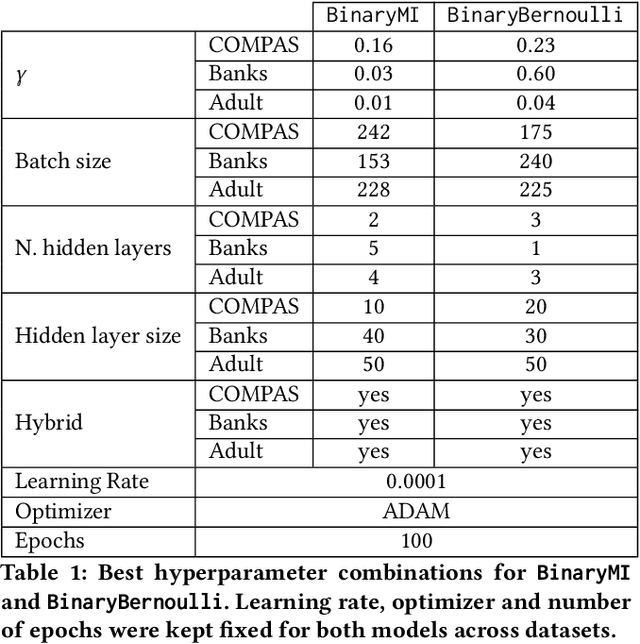
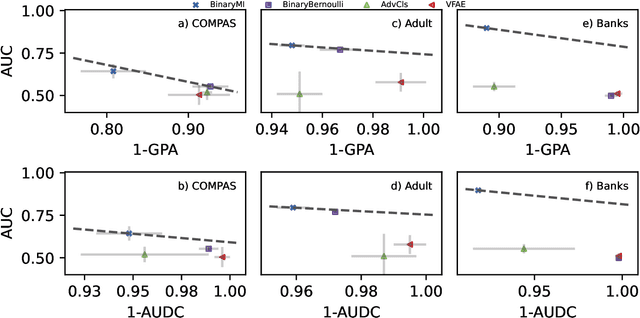
Representation learning algorithms offer the opportunity to learn invariant representations of the input data with regard to nuisance factors. Many authors have leveraged such strategies to learn fair representations, i.e., vectors where information about sensitive attributes is removed. These methods are attractive as they may be interpreted as minimizing the mutual information between a neural layer's activations and a sensitive attribute. However, the theoretical grounding of such methods relies either on the computation of infinitely accurate adversaries or on minimizing a variational upper bound of a mutual information estimate. In this paper, we propose a methodology for direct computation of the mutual information between a neural layer and a sensitive attribute. We employ stochastically-activated binary neural networks, which lets us treat neurons as random variables. We are then able to compute (not bound) the mutual information between a layer and a sensitive attribute and use this information as a regularization factor during gradient descent. We show that this method compares favorably with the state of the art in fair representation learning and that the learned representations display a higher level of invariance compared to full-precision neural networks.

Fair Interpretable Representation Learning with Correction Vectors

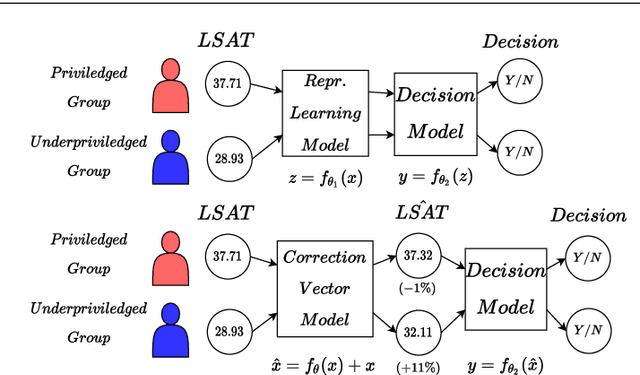
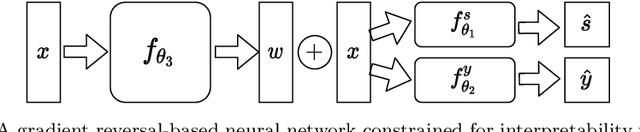
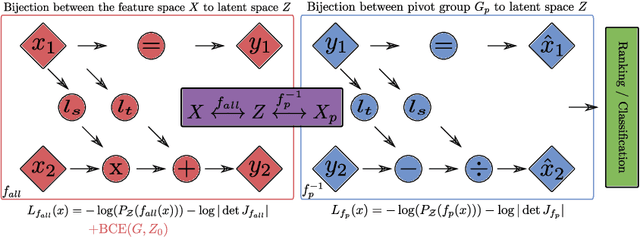
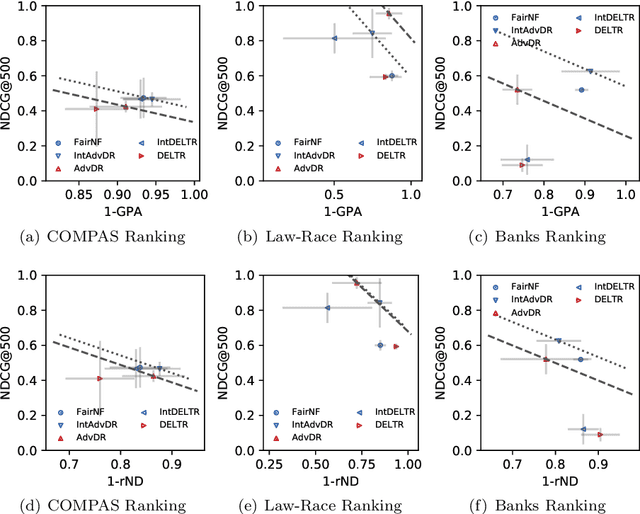
Neural network architectures have been extensively employed in the fair representation learning setting, where the objective is to learn a new representation for a given vector which is independent of sensitive information. Various representation debiasing techniques have been proposed in the literature. However, as neural networks are inherently opaque, these methods are hard to comprehend, which limits their usefulness. We propose a new framework for fair representation learning that is centered around the learning of "correction vectors", which have the same dimensionality as the given data vectors. Correction vectors may be computed either explicitly via architectural constraints or implicitly by training an invertible model based on Normalizing Flows. We show experimentally that several fair representation learning models constrained in such a way do not exhibit losses in ranking or classification performance. Furthermore, we demonstrate that state-of-the-art results can be achieved by the invertible model. Finally, we discuss the law standing of our methodology in light of recent legislation in the European Union.

Fair Interpretable Learning via Correction Vectors

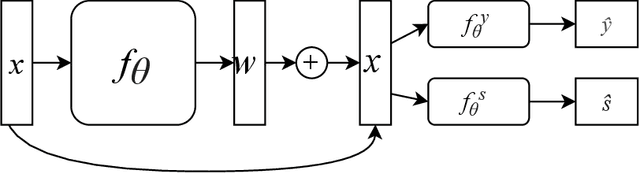
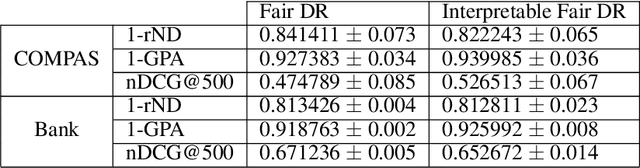
Neural network architectures have been extensively employed in the fair representation learning setting, where the objective is to learn a new representation for a given vector which is independent of sensitive information. Various "representation debiasing" techniques have been proposed in the literature. However, as neural networks are inherently opaque, these methods are hard to comprehend, which limits their usefulness. We propose a new framework for fair representation learning which is centered around the learning of "correction vectors", which have the same dimensionality as the given data vectors. The corrections are then simply summed up to the original features, and can therefore be analyzed as an explicit penalty or bonus to each feature. We show experimentally that a fair representation learning problem constrained in such a way does not impact performance.

Fair Group-Shared Representations with Normalizing Flows

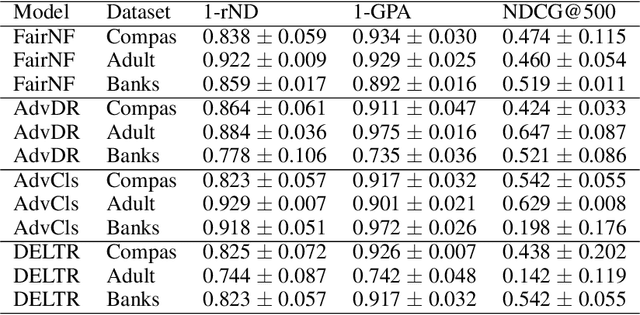
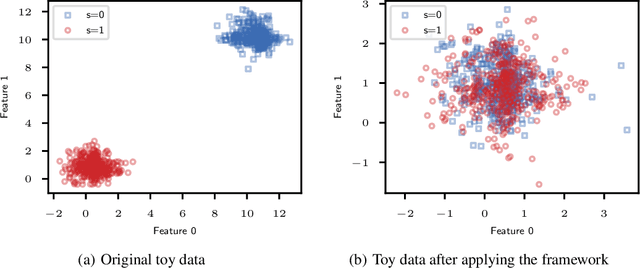
The issue of fairness in machine learning stems from the fact that historical data often displays biases against specific groups of people which have been underprivileged in the recent past, or still are. In this context, one of the possible approaches is to employ fair representation learning algorithms which are able to remove biases from data, making groups statistically indistinguishable. In this paper, we instead develop a fair representation learning algorithm which is able to map individuals belonging to different groups in a single group. This is made possible by training a pair of Normalizing Flow models and constraining them to not remove information about the ground truth by training a ranking or classification model on top of them. The overall, ``chained'' model is invertible and has a tractable Jacobian, which allows to relate together the probability densities for different groups and ``translate'' individuals from one group to another. We show experimentally that our methodology is competitive with other fair representation learning algorithms. Furthermore, our algorithm achieves stronger invariance w.r.t. the sensitive attribute.

Partitioned Least Squares

In this paper we propose a variant of the linear least squares model allowing practitioners to partition the input features into groups of variables that they require to contribute similarly to the final result. The output allows practitioners to assess the importance of each group and of each variable in the group. We formally show that the new formulation is not convex and provide two alternative methods to deal with the problem: one non-exact method based on an alternating least squares approach; and one exact method based on a reformulation of the problem using an exponential number of sub-problems whose minimum is guaranteed to be the optimal solution. We formally show the correctness of the exact method and also compare the two solutions showing that the exact solution provides better results in a fraction of the time required by the alternating least squares solution (assuming that the number of partitions is small). For the sake of completeness, we also provide an alternative branch and bound algorithm that can be used in place of the exact method when the number of partitions is too large, and a proof of NP-completeness of the optimization problem introduced in this paper.